
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Скалярное произведение двух векторовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Скалярным произведением двух векторов � и � называется произ- a b
Согласно определению � � � � � � a b = | a | × | b | × cos(a,^ b). (1.14)
Скалярное произведение � · � обращается в нуль, если один из a b � � сомножителей равен нулю или если векторы a и b перпендикуляр- ны (в этом случае косинус угла между векторами равен нулю).
ФИЗИЧЕСКИЙ СМЫСЛ СКАЛЯРНОГО ПРОИЗВЕДЕНИЯ Некоторые физические величины определяются как скалярное произведение векторных физических величин. �
где a — меньший угол между перемножаемыми векторами. Рис. 1.15 Если сила F и угол a постоянны, а тело движется прямолинейно, то работа силы на перемещении S А = S × F × cosa, (1.16) где S — модуль перемещения материальной точки. �
Рис. 1.16 � Элементарн�ым потоком dФ вектора магнитной индукции B через поверхность dS называется скалярное произведение
� � dФ = B × dS � где a — угол между вектором B = B × dS × cosa, (1.18)
верхности (рис. 1.17). Рис. 1.17
Вопросы и задания для самопроверки 1. Дайте определение скалярного произведения двух векторов. В каком случае скалярное произведение двух векторов положитель- но? Отрицательно? Равно нулю? 2. Поясните физический смысл скалярного произведения. 3. Изменится ли результат скалярного произведения двух векто- ров, если поменять местами перемножаемые векторы?
Примеры решения задач
� � �Найти скалярное произведение a × b, если длины векторов | a | = 2 м и | b | = 1 м, а угол ме�жду ними a = 120°. Дано: | � | = 2 м; | b | = 1 м; a = 120°. a � �
Найти: a × b. По определению скалярного произведения � � � � 1
� � 2 Ответ: скалярное произведение a × b = -1 м2.
Задача 1.8
Дано: | F | = 5 Н; | S | = 4 м; a = 45°. Найти: AF. По определению работа А силы F � � A = × = | | × | | × cosa = 4 × 5 × = 10 × » 14,1 Дж.
Ответ: работа силы AF» 14,1 Дж. Задача 1.9 Автомобиль массой m = 1000 кг перемещается прямолинейно под действием с�илы тяги F �= 5000 Н. Найти работу А, совер�шаемую си-
mg на перемещении S = 1 км. Коэффициент трения m = 0,1. Уско- рение свободного падения g = 10 м/с2. Дано: m = 1000 кг; F = 5000 Н; S = 1 км = 1000 м; m = 0,1; g = 10 м/с2.
Работа силы тяги: AF = F × S × cosa = 5000 × 10�00 × cos0° = 5000 × 1000 × 1= 5 × 106 Дж (между векторами силы тяги F и перемещения угол a = 0°). Работа силы трения:
= 0,1 × 1000 × 10 × 1000 × (–1) = –106 Дж (между векторами силы трения F тр и перемещения угол a = 180°). Работа силы тяжести: Amg = mg × S × cosa = 1000 × 10 × 1000 × cos90° 0 = 0 Дж (между век-
Работа силы реакции опоры: AN = N × S × cosa = mg × S × cosa = 1000 × 10 × 1000 × cos90° = = 1000 × 10 × �1000 × cos90° = 0 Дж (между векторами нормальной ре- акции опоры N и перемещения угол a = 90°�). � Ответ: работа, сове�ршаемая силами тяги F, трения F тр, нормаль- ной реакции опоры N и тяжести �, A = 5×106 Дж, A = -106 Дж, mg F AN = 0 Дж, Amg = 0 Дж соответственно. Задача 1.10 F тр Человек тянет сани, прикладывая силу F = 10 Н под углом a = 30° к горизонту. Под действием этой силы сани перемещаются горизонталь- но со скоростью v = 5 м/с. Найти мощность P, развиваемую силой. Дано: F = 10 Н; a = 30°; v = 5 м/с. Найти: Р. � �
2 � Ответ: развиваемая силой F
Задача 1.11 Рамка площадью S = 1 м2 рас- положена в однородном магнитном поле с индукцией В = 10–3 Тл так, что между векторами нормали � и � n индукции B угол a�= 60°. Определить поток Ф вектора B через рамку. Дано: S = 1 м2; a = 60°; В = 10–3 Тл. Найти: Ф. По определению магнитного потока Ф = В × S × cosa = 10–3 × 1 × cos60° = 0,5 × 10–3 Вб. Ответ: магнитный поток Ф = 0,5 × 10–3 Вб.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 553; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.10.220 (0.009 с.) |




 a × b = | a | × | b | × cosa = 2 × 1 × cos120° = 2 × 1 × (-) = -1 м2.
a × b = | a | × | b | × cosa = 2 × 1 × cos120° = 2 × 1 × (-) = -1 м2.
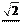 F S F S F 2
F S F S F 2
 Мощность P= F × v = F× v × cosa =
Мощность P= F × v = F× v × cosa = = 10 × 5 × cos30° = 10 × 5 × = 42 Вт.
= 10 × 5 × cos30° = 10 × 5 × = 42 Вт. мощность P = 42 Вт.
мощность P = 42 Вт.


