
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Динамика механических гармонических колебанийВыясним природу сил, создающих гармонические колебания. По второму закону Ньютона проекция силы, действующей на материаль- ную точку, с учетом (6.4), равна F = ma = - A w2 m sin(w t + j) = - m w2 x. (6.5) 0 0 0 0
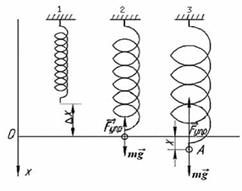
новесия. Рассмотрим колебания груза, висящего на пружи- не (рис. 6.3) 1. Если пружина растя- нута, то координата гру- за отрицательна, следова- тельно, проекция силы на ось х положительная. Это возможно, когда вектор силы параллелен оси х и направлен к точке равно- весия. Рис. 6.3 2. Если пружина сжата, то координата груза положительна, сле- довательно, проекция упругой силы на ось х отрицательна. Это воз- можно, когда вектор силы антипараллелен оси х и направлен к точке равновесия. В положении равновесия сила, вызывающая колебания, на материальную точку не действует, т. е. при х = 0, F = 0.
Таким образом, условию (6.5) удовлетворяют упругие силы. Гар- монические колебания могут быть вызваны также силами, которые не являются упругими по своей природе. Вывод: силы, не являющиеся упругими по своей природе, но подоб- ные упругим по характеру зависимости от координаты, называются квазиупругими. Ниже приведены примеры колебаний систем, совершающихся в отсутствии сил трения и сопротивления среды.
Пружинный маятник Пружинным маятником называют систему, состоящую из упру- гой невесомой пружины с коэффициентом упругости k и груза мас- сой m. На рис. 6.3 показаны: 1 — естественная длина пружины; 2 — со- стояние равновесия маятника; 3 — мгновенное состояние колеблю- щейся системы. Составим дифференциальное уравнение колебаний пружинного маятника и найдем его решение. Начало координат совместим с по- ложением равновесия маятника (положение 2 рис. 6.3). Ось х напра-
вим верти�кально вниз. На груз действует сила тяжести и сила уп- ругости F у¢пр. В положении равновесия векторная сумма сил, дейст- вующих на груз, равна нулю � � mg + F у¢пр = 0. Проекция векторного уравнения на ось х - F у¢пр+ mg = 0 или k Ä x = mg, (6.6) где Ä x — деформация пружины в состоянии равновесия, k — коэф- фициент упругости. Если груз отклонить от положения равновесия в ту или иную сторону, то результирующая сила, действующая на тело, не равна нулю. По второму закону Ньютона система придет в дви- жение с ускорением а � � � mg + F упр = ma.
лен оси x, то проекция данного векторного уравнения на ось x име- ет вид
d 2 x
dt 2
, получим 0 m d 2 x
dt 2 0 Второй закон Ньютона, записанный в форме (6.7), есть диффе- ренциальное уравнение собственных колебаний груза на пружине в отсутствии силы сопротивления. Для решения этого уравнения вос- пользуемся методом Эйлера. По этому методу решение уравнения (6.7) выберем в виде x (t) = Ce a t, где С — произвольная константа, a — неизвестная константа. Для нахождения этих констант подставим a t dx (t) a d x (t) a
x (t) = Ce, = C a e t, dt dt 2 = C a2 e t в (6.7), получим тождество C a2 e a t + w2 Ce a t = 0 или Ce a t (a2 + w2) º 0. 0 0 та a:
= ± i w0,
Двум значениям корня a1,2 соответствуют два частных решения. Общее решение находится как линейная комбинация двух частных решений x = C * e + i w0 t + C * e - i w0 t = ⎡т.к. e ± i w0 t = cosw t ± i sin w t ⎤= 1 2 ⎣ 0 0 ⎦
Введем новые обозначения: C * + C * = C, iC * - iC * = C, получим 1 2 1 1 2 2 x = C 1cos w0 t + C 2 sin w0 t. (6.8) Решение (6.8) запишем в форме
x = A sin(w0 t + j0) (6.9) То, что выражения (6.8) и (6.9) эквивалентны друг другу, следует из тригонометрического тождества A sin(w0 t + j0) = A (cosw0 t sin j0+ sin w0 t cosj0). (6.10) Из (6.8), (6.9) и (6.10) следует C 1 cos w0 t + C 2 sin w0 t = A cos w0 t sin j0 + A sin w0 t cosj0. Приравняв соответствующие коэффициенты при одних и тех же тригонометрических функциях, получим C 1 = A sin j0, C 2 = A cos j0,
Константы С 1 и С 2 находят из начальных условий, при этом луч- ше воспользоваться уравнением (6.8). При t = 0, x = х, dx = v, где x — начальная координата тела, v —
0 dt 0 0 0 начальная скорость. Подставив начальные условия в уравнения x = C 1 cos w0 t + C 2 sin w0 t, dx = v = - C w
sin w t + C w cosw t, получим dt 1 0 0 2 0 0
1 0 2 Отсюда амплитуда и начальный сдвиг фазы равны
A =, j0 = arctg 0 0. v Уравнение колебания груза на пружине имеет вид
x = x 2 + 0 sin(w t + arctg 0 0). (6.11)
0 0 Зависимости скорости и ускорения груза от времени найдем, взяв производную от (6.9):
x dt d 2 x 0 cos(w0 t + j0), a = = - A w2 sin(w t + j).
x dt 2 0 0 0 Кинетическая энергия груза m v2 mA 2w2 W = = 0 cos2 (w t + j),
K 2 2 0 0 2 2
Циклическая частота колебаний кинетической энергии равна 2w0, так как cos2 (w t +j) =1+ cos 2(w0 t + j0).
0 0 2 Потенциальная энергия груза kx 2 m w2 x 2 m w2 A 2 W = = 0 = 0 sin2 (w t + j),
П 2 2 2 0 0 совершающего гармонические колебания под действием силы упру- m w2 A 2 гости пружины, периодически изменяется от 0 до 0 с цикли- ческой частотой 2w0. Полная энергия груза
m w2 A 2
W = WК + WП = m w2 A 2
m w2 A 2 = cos2 (w t +j) + 0 sin2 (w t +j) = 0
(6.12) 2 0 0 2 0 0 2 — величина постоянная. Колебания любой физической величины, характеризующей мате- матический маятник, включая смещение х груза, записанное в фор- ме (6.11), называют собственными незатухающими колебаниями. Ве-
частотой и периодом колебаний маятника соответственно. Чем боль- ше масса груза m и меньше коэффициент упругости k пружины, тем медленнее происходят колебания. Полная энергия колеблющегося груза остается постоянной, так как движение происходит без прито- ка и без потерь энергии.
Физический маятник Физический маятник — абсолютно твердое тело, совершающее ко-
зонтальной оси z, не проходящей через центр тяжести тела. Сила тяже- сти приложена к центру тяжести тела, расположенном на расстоянии d от оси вращения (рис. 6.4). Колебательное движение физического маят-
Составим дифференциальное уравнение колебаний маятника и найдем его решение. Уравнение движения и закон движения запи- шем в скалярной форме. В качест- ве переменной величины выберем угловое смещение j. Это угол от- Рис. 6.4 клонения маятника от положения равновесия. Пусть маятник откло- нен от положения равновесия на малый угол j. При малых углах си- лой сопротивления среды можно пренебречь. Запишем основное уравнение динамики вращательного движения (второй закон Ньютона для вращательного движения) (см. гл. 5) M (m �) = J e, (6.13)
где Mz (m �) — момент силы тяжести относительно оси z, Jz – мо- мент инерции маятника относительно оси вращения z, e = ловое ускорение маятника. d 2j
Пусть в данный момент времен�и приращение угла d j >�0. В этом случае векторы угловой скорости w и углового ускорения e направ- лены вдоль оси z и параллельны этой оси. Так как сила тяжести по-
следует приписать знак минус (–), т. е.
где h = d sin j — плечо силы тяжести (рис. 6.4). Плечо — кратчайшее расстояние от линии действия силы до оси вращения z.
Дифференциальное уравнение движения физического маятника (6.13) принимает вид - mgd sin j = Jz d 2j
При малых углах j функцию sinj можно разложить в степен- ной ряд j3 j5 j2 n +1 sin j = j - + - ××× + (-1) n
+...
(6.15) 3! 5! (2 n + 1)! Если ограничиться первым членом разложения (6.15) и обозна- чить mgd =w2,
z то уравнение (6.14) примет вид
dt 2 0
0. (6.16) Уравнение (6.16) аналогично уравнению (6.9), следовательно, и решения уравнений одинаковы. Таким образом, при малых углах j колебательное движение фи- зического маятника, как и колебательное движение пружинного ма- ятника, является гармоническим, а именно j = jmax sin(w0 t + a0). (6.17) где jmax — максимальное значение углового смещения маятника от положения равновесия, a0 — начальное значение фазы. Циклическая частота и период колебания физического маятника вычисляются со- ответственно по формулам w0 = T = 2p= 2p. (6.18)
При малых угловых смещениях период колебания маятника не за- висит от амплитуды jmax и начальных условий движения. Формулы (6.18) могут быть использованы для экспериментально- го нахождения момента инерции тел сложной формы относительно выбранной оси z.
Рис. 6.5 Математический маятник
Математический маятник представ- ляет собой предельный случай физиче- ского маятника, вся масса которого со- средоточена в точке. Тогда расстояние от точки приложения силы тяжести до оси вращения равно длине нити l (рис. 6.5). Так как d = l, то момент инерции и циклическая частота такого маятника относительно оси вращения равны соответственно
mgl =
. (6.19) Дифференциальное уравнение колебаний математического маят- ника при отсутствии сопротивления среды такое же, как и для физи- ческого маятника и имеет вид d 2j+ w j =
dt 2 0 0. Таким образом, при малых углах отклонения j от вертикали дви- жение математического маятника представляет собой гармоническое колебание, описываемое формулой (6.10) j = jmax sin(w0 t + a0), (6.20)
Период колебаний математического маятника вычисляется по формуле
w0
Период колебаний не зависит от массы маятника m и амплитуды углового смещения jmax. Математический маятник используется в технике. Например, в геологии по измеренным значениям Т и l вычисляют ускорение сво- бодного падения для данной местности. Если в земной коре на ис- следуемой территории имеется неоднородность, то величина g отли- чается от стандартного значения. По этой аномалии можно предпо- ложить наличие полезных ископаемых.
Вопросы и задания для самопроверки 1. Как изменится частота, максимальная скорость, максимальное ускорение и полная механическая энергия гармонических колебаний, если удвоить амплитуду колебаний? 2. Два тела с одинаковыми массами подвешены к двум одинаковым пружинам. Тела оттягивают вниз — одно на 10 см, другое на 20 см — и затем одновременно отпускают. Какое из них первым пройдет положение равновесия? 3. Отличается ли максимальное значение кинетической энергии груза пружинного маятника от максимального значения потенциаль- ной энергии деформированной пружины? 4. Отличается ли циклическая частота колебаний кинетической энергии от циклической частоты колебаний потенциальной энер- гий пружинного маятника? 5. Математический маятник длиной L = 1 м подвешен к потол- ку кабины, которая начинает опускаться вертикально с ускорением
6. Какую длину должен иметь математический маятник, чтобы его период колебаний был равен одной секунде? 7. Докажите, что скорость математического маятника достигнет максимального значения, если его угловое смещение равно нулю. 8. Твердое тело закреплено таким образом, что ось вращения z про- ходит через точку приложения силы тяжести. Является ли это тело физическим маятником? 9. Период колебаний физического маятника тем больше, чем боль- ше расстояние от точки приложения силы тяжести до оси вращения. Верно ли это утверждение?
Примеры решения задач Задача 6.4 Рассказ Мюнхгаузена: «Как-то, гуляя, я невзначай забрался в горы. Захотелось узнать, на какой высоте я нахожусь. К счастью, в моей до- рожной сумке оказались маятниковые часы. Держа их в правой руке неподвижно, я начал сравнивать ход механических часов с показа- ниями электронных часов на левой руке. За час маятниковые часы отстали от электронных на пять секунд, и я сразу понял, на какой вы- соте нахожусь». Вычислите эту высоту. Примечание: Маятник часов сделан из такого сплава, что длина его от температуры не зависит. Электронные часы — точные. Радиус Земли примите равным R = 6400 км. Дано: t = 1 ч = 3600 c; R = 6400 км = 6,4 · 106 м; Ä t = 5 c. Найти: h. Из второго закона Ньютона найдем ускорение свободного паде- ния gh на высоте h над поверхностью Земли (на тело массой m дейст- вует только гравитационная сила)
(R + h)2 = ma или gh = G M.
На поверхности Земли (h = 0) ускорение свободного падения равно
R 2 Таким образом, при подъеме на высоту h ускорение свободного падения уменьшается
gh GM R R 2. Период колебаний маятниковых часов на поверхности Земли и на высоте h равны соответственно
а их отношение T = 2p и Th
T = 2p,
R + h h где T = T (R + h). h R Так как при подъеме на высоту h ускорение свободного падения уменьшается, то период колебаний маятника на высоте h увеличит- ся на Ä T Ä T = T - T = T (R + h) - T = T h.
h R R Если за одно колебание на высоте h период T увеличивается на Ä T, то за время t, равное 3600 с, на этой же высоте суммарный пери- од колебания увеличится на Ä t, т. е.
т. е. Ä t = th или t T R h = R Ä t. t Ответ: высота, на которую поднялся Мюнхгаузена, равна 8889 м. Примечание: Полученная высота чуть больше высоты Джамалун- гмы (8848 м) — самой высокой вершины на Земле. Сомнений в пра- вильности расчетов не должно быть, поскольку при решении были приняты допущения Ä t = Ä T.
Задача 6.5 Насколько будут отставать за сутки часы с секундным маятником, если их перенести из подвала на верхний этаж здания? Расстояние между ними — 200 м. Дано: h = 200 м; tc = 24 · 3600 = 8,64 · 104 с. Найти: Ä t.
T 1 колебаний, где T 1 — период колебаний маятника в подвале. Если период коле- баний маятника на верхнем этаже обозначить Т 2, то за сутки часы отстанут на Ä t = N (T 2 - T 1). Периоды колебания часов до и после переноса равны
Отношение периодов , T 2 = 2p.
T 2 Из закона всемирного тяготения следует, что
2 = ⎟, g 1 R + h ⎠ где R — радиус Земли. Отсюда следует, что T = T R + h и Ä t = N (T - T) = Nh T.
2 1 R 2 1 R 1 Ответ: отставание часов за сутки при переносе их с подвала на верхний этаж 2,7 с.
Задача 6.6 Амплитуда гармонических колебаний груза пружинного маятника А = 2 см, полная энергия W = 0,3 мкДж. При каком смещении груза х от положения равновесия на груз действует сила F = 22,5 мкН? Дано: A = 2 см = 0,02 м; W = 0,3 мкДж = 3 · 10–7 Дж; F = 22,5 мкН = 2,25 · 10–7 Н. Найти: х. Запишем уравнение гармонических колебаний точки в общем виде x = A sin(w0 t + j0). Найдем скорость точки, взяв производную от функции х (t) по вре- мени
x dt 0 cos(w0 t + j0). Полная энергия системы, равна сумме потенциальной и кинети- ческой энергий kx 2 m v2 kA 2 mA 2w2 W = + x = sin2 (w t + j) + 0 cos2 (w t + j).
2 2 2
0 0 2 0 0 , получим 0 m kA 2
sin2 (w t + j) + mA 2 k
cos2 (w t + j) = kA 2
A 2. Модуль квазиупругой силы, дeйствующей на груз в процессе ко- лебаний, равен
A 2 Ответ: смещение груза х от положения равновесия при действии силы F = 22,5 мкН равно
Задача 6.7 FA 2
2 E Однородный диск радиуса R колеблется около горизонтальной оси, перпендикулярной плоскости диска и проходящей на расстоя- нии d от центра диска. Каков период его колебаний? Дано: R. Найти: T.
T = 2p, где d — расстояние от оси вращения до точки приложения силы тя- жести. Согласно теореме Штейнера момент инерции I относитель- но оси, не проходящей через цент тяжести диска, где I 0 — момент инерции диска относительно оси, проходящей че- рез центр тяжести; m — масса диска; — расстояние между осями, равно d.
Ответ: период колебания физического маятника равен
Задача 6.8 Ареометр, имеющий форму цилиндрической трубки, массой m и с поперечным смещением S, помещенный в жидкость с плотностью r, совершает свободные колебания около положения равновесия. Вы- числить период колебания ареометра. Дано: m; S; r. Найти: Т. Ареометр — прибор для измерения плотности жидкости. Ось ци- линдрической трубки ареометра перпендикулярна ее поверхности.
На плавающий ареометр�действует сила тяжести, направленная вниз, и сила Архимеда FA, направленная вертикально вверх. В по- ложении равновесия mg = r gSh, где Sh — объем погруженной части прибора. Если погрузить ареометр на глубину h + x, то условие равновесия нарушится и, на ареометр будет действовать результирующая сила F = r gSh + r gSx - mg = r gSx. Так как r, g, S — константы, то F = kx, где k = r gS. Результирую- щая сила, действующая на ареометр, подобна упругой силе, действую- щей груз, висящий на пружине. Силы, не являющиеся упругими по своей природе, но подобные упругим силам по характеру зависимо- сти от координаты, называются квазиупругими. Под действием ква- зиупругой силы движение ареометра описывается такими же уравне- ниями, как и пружинный маятник. Следовательно, период колеба- ния ареометра можно вычислить по формуле
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 946; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.70.63 (0.005 с.) |
 Вывод: сила, вызывающая гармонические колебания, пропорциональ- на смещению колеблющейся точки от положения равновесия и всегда направлена положению рав-
Вывод: сила, вызывающая гармонические колебания, пропорциональ- на смещению колеблющейся точки от положения равновесия и всегда направлена положению рав- mg - k (Ä x + x) = m.
mg - k (Ä x + x) = m. С учетом (6.6), обозначив w2 = k
С учетом (6.6), обозначив w2 = k + w2 x = 0. (6.7)
+ w2 x = 0. (6.7)

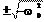 a1,2 =
a1,2 = где i — мнимая единица, (i =).
где i — мнимая единица, (i =). A = C 2 + C 2, j = arctg C 1.
A = C 2 + C 2, j = arctg C 1.


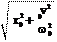 x w
x w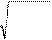 v2 x w
v2 x w v = dx = A w
v = dx = A w

 совершающего гармонические колебания, изменяется от 0 до m w0 A.
совершающего гармонические колебания, изменяется от 0 до m w0 A.


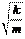
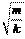 личины w0= и T = 2p называют собственной циклической
личины w0= и T = 2p называют собственной циклической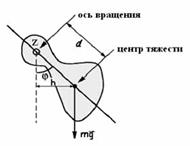 ника удобнее всего изучать, исполь- зуя основное уравнение динамики вращательного движения.
ника удобнее всего изучать, исполь- зуя основное уравнение динамики вращательного движения. dt 2 — уг-
dt 2 — уг- dt 2. (6.14)
dt 2. (6.14)



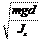

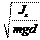 w0
w0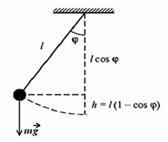 Математический маятник — мате- риальная точка, подвешенная на не- весомой нерастяжимой нити и совер- шающая колебания в вертикальной плоскости под действием силы тяже- сти (рис. 6.5).
Математический маятник — мате- риальная точка, подвешенная на не- весомой нерастяжимой нити и совер- шающая колебания в вертикальной плоскости под действием силы тяже- сти (рис. 6.5).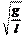
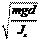 w0= =
w0= =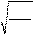 ml 2
ml 2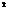

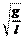 в которой w0=.
в которой w0=.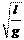 T = 2p = 2p. (6.21)
T = 2p = 2p. (6.21) a = g. Определить период T малых колебаний маятника.
a = g. Определить период T малых колебаний маятника. G Mm
G Mm (R + h)2
(R + h)2 g = G M.
g = G M.




 T = =
T = =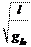
 = R,
= R,
 Ä t = Ä T
Ä t = Ä T Маятник часов за сутки должен совершить N = tc
Маятник часов за сутки должен совершить N = tc T 1 = 2p
T 1 = 2p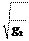

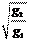 T 1 =.
T 1 =.


 Учитывая, что w2 = k
Учитывая, что w2 = k W =
W = 2 m
2 m .
. k =2 E
k =2 E F = kx или F = 2 E x.
F = kx или F = 2 E x. x = = 1, 5 см.
x = = 1, 5 см.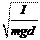 Период колебаний физического маятника
Период колебаний физического маятника Учитывая, что I = 1 mR 2, получим
Учитывая, что I = 1 mR 2, получим I = 1 mR 2 + md 2.
I = 1 mR 2 + md 2.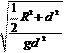 T = 2p.
T = 2p.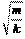
 T = 2p = 2p.
T = 2p = 2p. Ответ: период колебания ареометра T = 2p.
Ответ: период колебания ареометра T = 2p.


