
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вынужденные механические колебания
Рассмотрим колебания на примере пружинного маятника (рис. 6.11), который периодически подвергается внешним воздействиям в виде толчков, направленных в одну и ту же сторону и повторяющихся че- рез одинаковые промежутки времени. Переменную внешнюю силу, приложенную к телу на пружине и вызывающую механические ко- лебания, называют возмущающей силой�. Пу�сть возмущающая сила изменяется по гармоническому закону F = F 0 sin Ù t, где F 0, Ù — ам- плитуда и циклическая частота возмущающей сил�ы. Пусть на систе- му действуют сила тяжести �, сила упругости F, сила сопротив- � mg � � упр ления среды FR и возмущающая сила F = F 0 sin Ù t. Запишем второй закон Ньютона для груза � � � � � mg + F упр + FR + F 0 sin Ù t = ma. (6.44) Если повторить процедуры, проделанные в параграфе 6.6, с уче- том возмущающей силы, получим:
или d 2 x
dt 2 = - kx - r dx + F sin Ù t
d 2 x + b dx F 2 + w2 x = 0 sin Ù t.
(6.45) dt 2 dt 0 m Общее решение полученного неоднородного линейного дифферен- циального уравнения с постоянными коэффициентами (см. § 4.5 гла- вы «Математическое введение») складывается из двух слагаемых:
1) d 2 x
имеющего при w0 > b вид: + 2b dx
+ w2 x = 0,
2) частного решения неоднородного дифференциального урав- нения
+ 2b dx + w2 x = F 0 sin Ù t
имеющего вид: dt 2 dt 0 m Пояснение x 2 (t) = A sin (Ù t -q), При наличии вязкого сопротивления среды в линейных систе- мах (линейными системами называются системы, содержащие про- изводные и функции в первой степени) нет явления резонанса (о ре- зонансе будет сказано позже). Поэтому частное решение x 2(t) мож- но искать в виде правой части (6.45). Однако из-за наличия вязкого сопротивления среды, движение груза отстает по фазе на q от возму- щающей силы F. Вследствие этого частное решение неоднородного дифференциального уравнения ищется не в в виде x (t) = A sin Ù t, а в виде x 2 (t) = A sin(Ù t - q). Общее решение уравнения (6.45) равно сумме двух решений x (t) = x 1(t) + x 2 (t) или
Вынужденные колебания устанавливаются не сразу, так как груз одновременно совершает и собственные, и вынужденные колебания. Собственные колебания маятника x 1(t) постепенно затухают. Оста- ются только вынужденные колебания с частотой возмущающейся силы Ù
x (t) = A sin(Ù t - q). (6.45а) Чтобы найти A и q необходимо решение (6.45а) подставить (6.45). Однако возникают затруднения из-за того, что х (t) и правая часть (6.45) имеют разные фазы. Чтобы устранить затруднение, искусст-
венно преобразуем правую часть (6.45) таким образом, чтобы фазы были одинаковые. Пояснение к искусственному преобразованию Распишем по формуле синус суммы двух углов sin Ù t = sin(Ù t - q + q) = sin(Ù t - q) cosq + cos(Ù t - q) sin q. (6.45б) Подставим решение (6.45а) в (6.45), при этом в правой части урав- нения учтем преобразование (6.45б).
(6.45в)
Так как (6.45в) есть тождество, то приравняв соответствующие ко- эффициенты при sin(Ù t - q) и cos(Ù t - q), получим + A (-Ù2 + w2) = F 0 cosq,
0 m
m (6.45с) Для определения амплитуды А вынужденных колебаний возве- дем обе части уравнения (6.45с) в квадрат, сложим и извлечем ко- рень квадратный. Так как амплитуда величина положительная, то оставим только положительное значение корня
A 2 ⎡(w2 - Ù2)2 + 4b2Ù2 ⎤= 0, ⎣ 0 ⎦ m 2
(6.46) Для определения сдвига фазы q разделим второе уравнение на пер- вое (6.45с), получим
Отсюда tgq = 2bÙ. q = arctg 2bÙ. Таким образом, если внешняя возмущающая сила изменяется по гармоническому закону, то вынужденные колебания являются так- же гармоническими.
Частота вынужденных колебаний совпадает с частотой возмущаю- щей силы Ù и не зависит от свойств колеблющейся системы и сре- ды (w0 и b). Вынужденные колебания даже при наличии сопротивления среды являются незатухающими. Амплитуда вынужденных колебаний мо- жет быть очень большой при малых значениях сопротивления сре- ды и возмущающей силы, если частота возмущающей силы Ù близ- ка к собственной частоте w0. И наоборот, амплитуда вынужденных колебаний может быть сколь угодно малой при больших значениях возмущающих сил, если часто- та возмущающих сил Ù сильно отличается от частоты w0 (т. е. Ù << w0либо Ù >> w0).
Амплитуда А вынужденных колебаний и величина q, определяю-
зависят, но зависят от соотноше- ния частот возмущающей силы и собственных колебаний. Рассмотрим зависимость ам- плитуды вынужденных колеба- ний А от частоты возмущающей силы Ù (рис. 6.14) при фиксиро- ванных F 0, w0 и m. Если Ù = 0 (сила F постоянна), то Рис. 6.14
= Ä, где Ä — статическая деформация. Если Ù = ¥, то A ® 0. Если b = 0, то при Ù = w0 А стремиться к бесконечности. Это имеет место, когда коэффициент сопротивления среды ра- вен нулю. Если b ¹ 0, то при некоторой определенной для данного пружин- ного маятника частоте возмущающей силы Ùрез < w0 амплитуда ко- лебаний А достигает максимального значения. Явление резкого возрастания амплитуды установившихся вынуж- денных колебаний при приближении частоты Ù внешней возмущающей силы к некоторой характерной для данного маятника частоте Ùрез по- лучило название механического резонанса. Чтобы найти резонансную частоту Ùрез для рассматриваемой сис- темы, необходимо исследовать подкоренное выражение (6.46) на экс- тремум (при этом следует иметь в виду, что экстремумы амплитуды A (Ù) и подкоренного выражения f (Ù) противоположны). Возьмем производную от подкоренной функции по частоте Ù и приравняем ее к нулю df (Ù) = 2(-2Ù)(w2 - Ù2) + 8b2Ù = 0. d Ù 0 Из полученного равенства находится то значение аргумента Ù, при котором подкоренное выражение будет либо максимальным, либо минимальным: -4Ùw2 + 4Ù3 + 8Ùb2 = 4Ù(-w2 + Ù2 + 2b2) = 0. 0 0
Так как Ù — существенно положительная величина, то берем толь- ко положительное значение корня.
гумента Ù = , необходимо взять вторую производную от функции f = f (Ù) и исследовать ее знак. d 2 f
d 2 f
d Ù2 d Ù2 то функция f = f (Ù) — максимальна. d 2 f = -4w2 + 12Ù2 + 8b2 = -4w2 + 12w2 - 24b2 + 8b2 =
⎣⎢ 0 ⎦⎥ = 8w2 -16b2 = 8(w2 - 2b2) = 8Ù2. 0 0
d Ù2 = 8Ù2 > 0, то при частоте Ù = подкорен- ное выражение f = f (Ù) принимает минимальное значение, следо- вательно, амплитуда колебаний А достигнет наибольшего (макси- мального) значения.
Таким образом, амплитуда вынужденных колебаний А принима- ет максимальное значение, когда частота возмущающей силы равна Частоту возмущающей силы, при которой амплитуда А достигает
Ùрез = . 6.47 Из формулы видно, что резонансная частота Ùрез меньше частоты собственных незатухающих колебаний маятника w0. З ависимость A = A (Ù) называется резонансной кривой. На рис. 6.14 изображены резонансные кривые, соответствующие различным зна- чениям коэффициента затухания (b0= 0, b1< b2< b3). Максимум ре- зонансной кривой тем выше и острее, чем меньше b. При отсутствии сопротивления среды (b0= 0) амплитуда бесконечна (A ® ¥).
При сооружении строительных объектов в сейсмических зонах не- обходимо учитывать резонансные явления. Собственная частота объ- екта должна отличаться от частоты колебаний земной коры, наблю- даемой в данной местности. В этом случае при землетрясении есть вероятность сохранения построенных зданий.
Вопросы и задания для самоподготовки 1. Почему незатухающие колебания в реальных системах могут быть только вынужденными? 2. Почему важен случай гармонического внешнего воздействия на колебательную систему? 3. Какие процессы наблюдаются при вынужденных колебаниях, когда частота возмущающей силы Ù приближается к собственной частоте w0? 4. Что такое резонансная частота вынужденных колебаний, от чего она зависит? 5. Изменяется ли амплитуда вынужденных колебаний со време- нем при постоянной частоте возмущающей силы? 6. От каких параметров зависит амплитуда вынужденных коле- баний? 7. Может ли амплитуда вынужденных колебаний быть бесконеч- но большой?
8. Почему при увеличении частоты возмущающей силы, дейст- вующей на колеблющуюся систему, амплитуда вынужденных коле- баний достигает максимума, затем убывает?
Примеры решения задач Задача 6.14 Тело совершает затухающие колебания с максимальным значени- ем амплитуды А 0 = 7 см, начальной фазой j0 = 0, коэффициентом за- тухания b = 1,6 с–1. На это тело начала действовать внешняя перио- дическая сила, под действием которой установились вынужденные колебания. Уравнение вынужденных колебаний имеет вид x 2 (t) = 12 sin(10p t - 0, 75p) см. Найти уравнение (с числовыми коэффициентами) собственных затухающих колебаний. Дано: А 0 = 7 см; j0 = 0; b =1,6 с–1; x 2 (t) = 12 sin(10p t - 0, 75p) см. Найти: x (t). Запишем уравнение затухающих колебаний в общем виде
Чтобы записать приведенное уравнение с числовыми коэффици- ентами, необходимо вычислить циклическую частоту затухающих колебаний w. По тексту дано уравнение вынужденных колебаний x 2 (t) = 12 sin(10p t - 0, 75p) см, где А = 0,12 м, Ù = 10p, j = –0,75 p. Обозначим начальную фазу вынужденных колебаний — q и вы- числим tgq = tg(-0, 75p) = -1. Начальная фаза вынужденных колебаний вычисляется по фор- муле (см. § 6.7) tgq = - 2bÙ.
Приравняв правые части представленных выражений, получим
-1 = - 2bÙ.
Ответ: уравнение затухающих колебаний системы с числовыми коэффициентами имеет вид x (t) = 7 e -1,6 t sin10, 5p t (см).
Задача 6.15 Период затухающих колебаний системы T = 0,1 с, а отношение амплитуд первого и одиннадцатого колебаний m = A 1
= 21. Опреде- лить резонансную частоту Ù p, коэффициент затухания b и на сколь- ко резонансная частота меньше собственной частоты Äw данной ко- лебательной системы. Дано: T = 0,1 с; m = Найти: Ù p, b, Äw. A 1
= 21.
Ù p = и , (1)
T 2 = 4p2 , w2 - b2 = 4p2 , w =
. (2)
T 2 0 Из (1) и (2) находим резонансную частоту
Для нахождения коэффициента затухания b запишем уравнение, связывающее первую и одиннадцатую амплитуды с учетом того, что время между первой и одиннадцатой амплитудой составляет 10 пе- риодов и равно t = 10 T.
A = A e -b(t +10 T). 11 0
Из уравнений следует
A = A e -b10 T, 11 1
= 5 b10 T = m. Прологарифмировав последнее уравнение, получим ln m = b10 T. Вычислим первую неизвестную величину b
10 T Расчетные формулы и величины резонансной и собственной час- тоты системы равны соответственно
Ù p = T 1-⎜⎝ 2p10 T ⎟⎠ = 62, 76 рад/с, w0 = b2 +4p = 62,83 рад/с. Ответ: резонансная частота Ù p = 62,76 рад/с, коэффициент зату- хания b = 3.04, резонансная частота Ù p меньше собственной w0на Äw = 0,07 рад/с. Собственная частота колебаний системы w0= 62,83 рад/с.
МЕХАНИЧЕСКИЕ ВОЛНЫ
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 638; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.195.206 (0.103 с.) |
 m
m dt 0
dt 0

 dt 2
dt 2 dt
dt d 2 x
d 2 x
 2b A Ù = F 0 sin q.
2b A Ù = F 0 sin q. A = F 0.
A = F 0. щая сдвиг фаз между вынужденными колебаниями и возмущающей силой, от начальных условий не
щая сдвиг фаз между вынужденными колебаниями и возмущающей силой, от начальных условий не A = F 0
A = F 0 Ù = ±.
Ù = ±. Чтобы выяснить, какой экстремум имеет место при значении ар-
Чтобы выяснить, какой экстремум имеет место при значении ар-

 d Ù2 ⎡Ù= w2 - 2b2 ⎤ 0 0 0
d Ù2 ⎡Ù= w2 - 2b2 ⎤ 0 0 0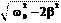 d 2 f
d 2 f Так как
Так как
 максимального значения, называют резонансной частотой.
максимального значения, называют резонансной частотой.
 Собственная частота системы равна w0=. Частота затухающих колебаний равна w =
Собственная частота системы равна w0=. Частота затухающих колебаний равна w =
 w = = = 10, 5p.
w = = = 10, 5p. A 11
A 11 Резонансная частота вынужденных колебаний и период затухаю- щих колебаний определяются по формулам
Резонансная частота вынужденных колебаний и период затухаю- щих колебаний определяются по формулам T = 2p.
T = 2p. Собственная частота w0колеблющейся системы равна
Собственная частота w0колеблющейся системы равна

 Ù p = =.
Ù p = =. b = ln m = 3, 04.
b = ln m = 3, 04. 2p ⎛ ln m ⎞ 2
2p ⎛ ln m ⎞ 2


