
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закон сохранения и изменения импульса
Замкнутая система Закон сохранения импульса является прямым следствием второго и третьего законов Ньютона. Для изолированного тела этот закон яв- ляется очевидным следствием второго закона Ньютона: если на тело не действуют никакие силы, то его скорость, а значит, и импульс ос-
таются постоянным. В случае взаимодействия тел закон сохранения импульса является следствием обоих законов Ньютона (если тела взаимодействуют, но не подвергаются действию внешних сил). Рассмотрим замкнутую систему (взаимодействуют только тела,
Если скорости тел �, �, �, …, внутренние силы, действующие меж- � � v �1 v 2� v 3 � ду ними F 12, F 13, … F 21, F 23, … (Fik – сила, действующая на i -е тело cо стороны k -го), то уравнения второго закона Ньютона для каждого из этих тел имеют вид ⎧ d (m v �) = �
� � + +... +, ⎪ dt 1 1 F 12 F 13 F 1 n
⎨ dt ⎪... ⎪ d � � � �
� � � �
(3.53) ⎪ (m v) = F + F +... + F. ⎪⎩ dt n n n 1 n 2 n, n -1 Складывая левые и правые части этих уравнений, получим d � � � � � � �
i i k i В правой части равенства (3.54), под знаком суммы, собраны все силы, действующие между телами замкнутой системы. Представим их в виде таблицы, в каждой строчке которой расположим только силы, приложенные к оп-ределенному телу ⎛0 � � � ... ⎞
F 13 F 1 n ⎟ () = ⎜21 0 F 23 ... F 2 n ⎟ (3.55) F ⎜............... ⎟ ⎜� � � ⎟ ⎝ F 1 n F 2 n... Fn, n -1 0 ⎠ Такая таблица в математике называется квадратной матрице�й раз- мера n ´ n с нулевыми диагональными элементами, так как Fii = 0, (i �= 1, 2�,..., n). Учитывая, что согласно третьему закону Ньютона Fik = - Fki, перепишем ее в другом виде
⎛ 0 � � � ... ⎞
F 13 F 1 n ⎟ () = ⎜ 12 0 F 23 ... F 2 n ⎟ (3.56) F ⎜............... ⎟
� ... 0 ⎝ F 1 n F 2 n Fn -1, n ⎠ Такая матрица называется кососимметрической, так как все ее элементы симметричны относительно диагонали и отличаются зна- ком. Складывая эти элементы попарно, получим сумму всех членов в правой части соотношения (3.54)
Fik = (Fi 1+ Fi 2 +... + Fii -1 + Fii +1 + Fin) = 0, (3.57) i k i т. е. полная сумма всех сил в замкнутой системе равна нулю. Следо- вательно, для всякой замкнутой системы выполняется равенство d ⎛ � ⎞ n �
i i =1 Последнее соотношение представляет собой закон сохранения им- пульса для замкнутой системы — полный импульс замкнутой систе- мы есть величина постоянная.
Незамкнутая система Если система материальных тел не является замкнутой и на вхо-
«внешних» тел, то импульс системы не является величиной постоян- ной. Система уравнений движения для всех тел имеет вид ⎧ d (m v) = + +... + +, ⎪ dt 1 1 F 12 F 13 F 1 n Ф 1 ⎪ d
⎪...
(3.59)
⎪⎩ dt
Если теперь сложить все эти уравнения, то получим
d å m v = å +å. dt i
i i i, k Fik Фi i Сумма внутренних сил, согласно (3.57), равна нулю. Следовательно, d å m v = å , (3.60) dt i i i Фi i то есть производная от полного импульса незамкнутой системы рав- на геометрической сумме всех внешних сил, т. е. полный импульс не сохраняется. Поскольку уравнение (3.60) — векторное, то оно эквивалентно трем уравнениям для компонент импульса системы по трем коор- динатным осям d å mv = å Ф; d å mv = å Ф; d å mv = å Ф, dt i i ix ix i dt i i iy iy i dt i i iz iz i гдеå Фix,å Фiy,å Фiz — суммы компонент всех внешних сил по ка- i i i ждой из координатных осей. Если сумма компонент всех внешних сил, действующих на систему, в каком-либо определенном направ- лении, например в направлении оси х, равна нулю, то для этого на- правления d å mv = 0 ® d å mv = const. (3.61) dt i i ix dt i i ix Следовательно, компонента полного импульса системы в направ- лении, в котором не действуют внешние силы, есть величина посто- янная, и в этом направлении незамкнутая система ведет себя как замк- нутая. Согласно (3.60) полный импульс незамкнутой системы со- храняется, если действующая на нее результирующая внешняя сила равна нулю.
Отметим, что в микроскопическом мире атомов и молекул вто- рой и третий законы Ньютона не выполняются, а законы сохранения энергии и импульса, что подтверждается многочисленными экспери- ментальными данными, продолжают выполняться. Именно поэтому считается, что законы сохранения имеют более общий характер и рас- сматриваются как более фундаментальные, чем законы Ньютона.
Вопросы и задания для самопроверки 1. Дайте определение импульса тела. Импульс — величина век- торная или скалярная? 2. Представьте кинетическую энергию тела через его импульс и массу. 3. Выведите закон сохранения импульса для замкнутой и незамк- нутой систем материальных тел. 4. Почему силы трения, действующие в замкнутой системе, при- водят к нарушению закона сохранения импульса? 5. Почему закон сохранения импульса в механике нельзя считать самостоятельным законом? 6. Как выбрать пространственное направление, вдоль которого со- храняется компонента полного импульса системы? 7. В каком случае полный импульс незамкнутой системы сохра- няется? 8. Почему законы сохранения энергии и импульса считаются бо- лее фундаментальными, чем законы Ньютона?
Примеры решения задач Задача 3.15 В результате взрыва неподвижное тело распадается на три части. Две его части массами m 1 = 1 кг и m 2 = 2 кг разлетаются под прямым углом друг к другу с начальны- ми скоростями v 1 = 12 м/с и v 2 = 8 м/с. Тре- тья часть начинает движение со скоростью v 3 = 40 м/с. Найти ее массу m 3 и углы между направлениями движения частей тела. Дано: m 1 = 1 кг; m 2 = 2 кг; v 1 = 12 м/с; v 2 = 8 м/с; v 3 = 40 м/с. Найти: m 3, b. Согласно закону сохранения импульса «импульс до события равен импульсу по- сле события», т. е.
0 = � + m � + m �. m 1 v 1 2 v 2 3 v 3
Поскольку импульсы первых двух частей направлены под пря- мым углом, то импульс третьего осколка может иметь направление и длину только, как представлено на рисунке, т. е. он должен лежать на продолжении диагонали прямоугольника и совпадать с ней по дли- не. Используя теорему Пифагора, получим m 2 v 2 = (m v)2 + (m v)2. 3 3 1 1 2 2 Из последнего уравнения найдем массу третьего осколка
Углы между импульсами легко найти, используя следующие со- отношения:
m 2 v 2 m 2 v 2
m 2 v 2
mv
= 0, 5 кг; b = p - arctg 1 1 = 143°. m 2 v 2
СТОЛКНОВЕНИЯ ТЕЛ Движение сталкивающихся тел может быть рассмотрено на осно- ве законов Ньютона. Для этого необходимо знать силы, возникаю- щие при контакте тел, и как они изменяются при соударении. Одна- ко обычно представляет интерес конечный результат соударения, а не детали процесса, длящегося очень короткое время, и в большин- стве случаев его можно представить как мгновенное изменение ско- ростей соударяющихся тел. Так как два сталкивающихся тела, на которые не действуют силы со стороны других тел, представляют собой замкнутую систему, то к ним применимы законы сохранения импульса и энергии. Зная пара- метры движения тел до столкновения, и применяя законы сохране- ния, можно определить параметры движения тел после столкнове- ния, не привлекая соображения о том, как происходит само столк- новение.
Для иллюстрации рассмотрим центральный удар двух шаров. Удар называется центральным, если скорости сталкивающихся тел лежат на линии, соединяющей их центры тяжести.
Абсолютно неупругий удар Удар, после которого скорости обоих соударяющихся тел оказы- ваются одинаковыми, называется абсолютно неупругим. После тако- го соударения тела не восстанавливают своей формы. Таким свойст- вом обладают, например, мягкая глина, пластилин и многие другие пластичные тела. Случай абсолютно неупругого удара можно проде- монстрировать при помощи пластилиновых шаров, подвешенных на нитях одинаковой длины. После удара шары будут двигаться вместе с одинаковой скоростью. Если удар двух тел абсолютно неупругий, то требуется определить только их общую скорость после удара. Пусть массы сталкивающихся тел m и m, их скорости до удара � и �, а � — общая скорость по- 1 2 v 1 v 2 u сле удара. Согласно закону сохранения импульса импульс системы тел до столкновения ра- вен импульсу образовавшегося тела массой (m 1 + m 2) после столк-
m � + m � = (m + m) �. (3.62) Вектор его скорости после удара � �
m 1 + m 2 , (3.63) совпадает с прямой, вдоль которой направлены скорости тел до уда- ра. Поэтому равенство (3.63) в скалярной форме имеет вид
m 1 + m 2 Скорости в последнем равенстве следует считать совпадающими по знаку, когда они направлены в одну сторону, и противоположны- ми по знаку, когда они направлены в разные стороны. Из (3.64) сле- дует, что если шары движутся навстречу друг другу, то вместе они бу- дут двигаться в сторону движения шара с большим импульсом. Рассмотрим несколько частных случаев.
1. Если импульсы шаров равны по величине и направлены на- встречу друг другу � �
то после столкновения они остановятся, т. е. u = 0. 2. Если одно из тел сталкивается с неподвижным телом: v 1 > 0, v 2 = 0, то, согласно (3.64), их скорость после столкновения
m 1 + m 2 меньше скорости первоначально движущегося тела и совпадает с ней по направлению. 3. Если массы тел одинаковые m 1 + m 2, то скорость их совместно- го движения определяется соотношением
u = 1 (v + v).
2 1 2 � � В случае нецентрального удара обе скорости v 1 и v 2 можно раз- ложить на составляющие вдоль линии, соединяющей центры ша- ров, перпендикулярном направлении. Для составляющих вдоль ли- нии центров все будет обстоять так же, как и при центральном уда- ре. Они окажутся равными и для них можно записать соотношение (3.64), что и при центральном ударе. Для перпендикулярных состав- ляющих скоростей дело обстоит иначе. Их изменяют возникающие между телами силы трения, которые приведут к вращению шаров, и анализ движения существенно усложнится по сравнению с приве- денным выше. Поэтому закон сохранения импульса позволит опре- делить только составляющую результирующей скорости совместно- го движения в направлении линии центров шаров.
Вопросы и задания для самопроверки 1. Дайте определение абсолютно неупругого удара. Могут ли уп- ругие тела сталкиваться абсолютно неупруго? 2. Дайте определение центра тяжести материального тела, цен- трального и нецентрального удара. 3. Всякий ли абсолютно неупругий удар является центральным, а центральный — абсолютно упругим? 4. Математически проанализируйте частные случаи абсолютно не- упругого столкновения двух тел.
5. Обоснуйте утверждение, что шары, движущиеся навстречу друг другу, после абсолютно неупругого удара вместе будут двигаться в сто- рону движения шара с большим импульсом. 6. Может ли скорость тела, образованного после абсолютно не- упругого столкновения, превышать скорость каждого из тел до их столкновения?
Примеры решения задач Задача 3.16 Найти изменение Ä K кинетической энергии двух шаров массами m и m, имеющих скорости � и � после их центрального и абсолют- 1 2 v 1 v 2 но неупругого удара. Дано: m и m; �; �. 1 2 v 1 v 2 Найти: Ä K. Система уравнений для решения задачи имеет вид: m v 2 m v 2 K = 1 1 + 2 2 1 2 2
K 2 2
� 1 v 1 2 v 2
— кинетическая энергия шаров до их столкновения; (1) — кинетическая энергия шаров после их столкновения; (2) u = m 1 + m 2 — скорость шаров после их столкновения; (3) Ä K = K 1 - K 2 — изменение кинетической энергии шаров из-за столкновения. (4)
K 2 =
(m � + m �)2. (5) Подставляя (1) и (5) в соотношение (4), имеем 1 ⎡ (� + m �)2⎤ Ä K = ⎢ m v 2+ m v 2-
m 1 v 1 2 v 2 ⎥, 2 ⎣1 1 2 2
m 1 + m 2 ⎦ или, после приведения к общему знаменателю, Ä K = 1 ⎡(m + m)(m v 2+ m v 2) - (
� + m �)2 ⎤ 2(m 1 + m 2) ⎣
1 2 1 1 2 2 m 1 v 1 2 v 2 ⎦
Ä K = 1 (m 2 v 2 + m m v 2 + m m v 2 + m 2 v 2-
2(m 1 + m 2) 1 2 1 2 2 - m 2 v 2 - m 2 v 2 - 2 mm ��).
1 1 2 2 1 2 v 1 v 2 После простых преобразований имеем Ä K = m 1 m 2 (v 2+ v 2- 2 ��). (6)
2 (m + m 2) v 1 v 2 Окончательный результат имеет вид
m 1 m 2 (� - �)2. (7) v 1 v 2 2 (m 1 + m 2) В заключение отметим, что Ä K > 0, т. е. кинетическая энергия сис- темы тел до столкновения всегда превышает кинетическую энергию образующегося после столкновения тела, так как все множители в
(7) положительны. Согласно закону сохранения энергии (в общефи- зическом смысле) разность между этими энергиями превращается в эквивалентное количество тепловой энергии. Причем, согласно (6), количество тепловой энергии определяется взаимным направлени- ем начальных скоростей. Если скорости направлены навстречу друг другу (удар «лобовой»), то скалярное произведение скоростей отрица- тельно: �� = vv cos p = - vv < 0. Если же скорости тел направлены в v 1 v 2 1 2 1 2 �� одну сторону и одно тело догоняет другое, то v 1 v 2= v 1 v 2cos 0° = v 1 v 2> 0. Количество тепловой энергии, соответствующее каждому из этих слу- чаев, получим на основе соотношения (6) Ä K 1 = m 1 m 2
(v + v)2; Ä K = m 1 m 2
(v - v)2.
m 1 m 2 (v - v)2.
Задача 3.17
Резиновая пуля массой m 1 = 10 г, летящая горизонтально, абсолют- но неупруго соударяется с шаром массой m 2 = 0,2 кг, подвешенном на нити длиной L = 1 м. В результате удара образовавшееся тело откло- няется от вертикали на угол a = 30°. Найти скорость v 0 пули до уда-
Дано: m = 10 г; М = 0,2 кг; L = 1 м; a = 30°. Найти: v 0, v, Q. Систему уравнений для решения задачи неупругого столкнове- ния тел представим в виде
— закон сохранения импульса; (1) — закон сохранения энергии; (2) h = L - L cos a — высота подъема пули + шара над равновесным состоянием; (3) mv 2
(m + M) v 2 — количество образовавшегося 2 2
при ударе тепла. (4)
одной прямой, то уравнение (1) можно переписать в скалярной форме mv = (m + M) v ® v = ⎛ M + 1⎞ v. (5)
0 0 ⎜⎝ m ⎟⎠
. (6)
v = ⎛ M + 1⎞
. (7) 0 ⎜⎝ m ⎟⎠ Используя формулы (6) или (7), найдем выражение для количе- ства тепла Q = mM v 2 = M (M + m) gL (1- cos a), (8)
2(m + M) 0 m образовавшегося при столкновении тел.
После подстановки в формулы (6–8) численных значений пара- метров, определенных условиями задачи, получим v = 1,62 /с; v 0 = 34,02 м/с; Q = 5,5 Дж. Примечание. Теперь рассчитаем кинетические энергии пули до столкновения и тела (пуля + шар) в момент столкновения
K 0 5,8 Дж; K 1 2 2 =(m + M) v 2
= 0,3 Дж; и из отношений
K 1 5,8 K 1 5,8
= 1,62 м/с;
= 34,02 м/с; 0 ⎜⎝ m ⎟⎠
m
= 5,5 Дж.
Абсолютно упругий удар Абсолютно упругий удар — кратковременное взаимодействие тел, после которого в обоих телах не остается никаких деформаций и вся кинетическая энергия, которой обладали тела до удара, после удара снова превращается в кинетическую энергию. После такого соуда- рения тела полностью восстанавливают свою форму. Реальные тела не обладают такими идеально упругими свойствами, но в некоторых из них возникающие после удара деформации настолько малы, что с высокой степенью точности ими можно пренебречь. Таковы, напри- мер, хорошие сорта стали и стекол, слоновая кость и т. д. Если удар можно считать абсолютно упругим, то для скоростей до удара и после удара должны быть справедливы уравнения, выражаю- щие законы сохранения импульса и энергии
m v 2 m v 2 m u 2 m u 2 1 1 + 2 2 = 1 1 + 2 2, (3.66) 2 2 2 2 где m, m — массы сталкивающихся шаров; �, � — их скорости до 1 � 2 � v 1 v 2 удара; u 1 и u 2 — их скорости после удара. Для простоты анализа остановимся на случае центрального уда- ра. Тогда уравнение (3.65) можно рассматривать как скалярное (все скорости до и после удара направлены по линии центров, и их раз- ные направления различаются только знаками) и переписать систе- му уравнений в таком виде: ⎧⎪ m 1(v 1- u 1) = m 2(u 2- v 2); ⎨ m (v 2 - u 2) = m (u 2 - v 2). ⎩⎪ 1 1 1
2 2 2 Разделив второе уравнение на первое, и перегруппировав слагае- мые, получим
u 1 - u 2 = - v 1 + v 2. (3.68) Неизвестные скорости u 1 и u 2 найдем, воспользовавшись прави- лом Крамера, хотя систему уравнений (3.67), (3.68) можно решить и другими способами. Для этого запишем следующие определители:
Ä u 1= Ä= m 1;
- v 1 + v 2; m 2; -1; m 2; -1; = -(m 1 + m 2);
m 1 v 1 + m 2 v 2; = -(m - m) v - 2 m v. u 2 1; - v 1 + v 2; 2 1 2 1 1
Ä u (m - m) v + 2 m v Ä m 1 + m 2 Ä u (m - m) v + 2 m v Ä m 1 + m 2
В таком виде полученные выражения для анализа достаточно сложны. Наиболее интересные частные случаи рассмотрим ниже в примерах решения задач.
Вопросы и задания для самопроверки 1. Дайте определение абсолютно неупругого удара. Может ли не- упругое тело сталкиваться с упругим абсолютно упруго или абсолют- но неупруго? 2. В чем сходство и отличие абсолютно упругого и абсолютно не- упругого ударов? 3. При рассмотрении абсолютно упругого удара закон сохранения энергии используется в общефизическом или механическом смысле? 4. Решите систему уравнений (3.65) и (3.66) любым способом, от- личным от приведенного в тексте. 5. В формулы (3.69) и (3.70) входят модули скоростей взаимодей- ствующих тел или их проекции?
Примеры решения задач Задача 3.18 Найти скорости u 1 и u 2 двух шаров массами m 1 и m 2 после централь- ного и абсолютно упругого удара, если их скорости до удара v 1, v 2, и сумма импульсов шаров до удара равна нулю, т. е. m 1 v 1 + m 2 v 2 = 0. Ис- следуйте характер движения шаров после удара. Дано: m 1; m 2; v 1; v 2; m 1 v 1 + m 2 v 2 = 0. Найти: u 1, u 2. При решении задачи проведите последовательные математиче- ские преобразования для центрального и абсолютно упругого удара двух шаров и выведете следующую систему уравнений: m 1 v 1 + m 2 v 2 = 0; (1) u 1 – u 2 = – v 1 + v 2, (2) которая легко получается из уравнений (3.67) и (3.68), полагая в пер- вом из них m 1 v 1 + m 2 v 2 = 0. Решите систему самостоятельно и сравни- те полученные результаты с приведенными ниже. Для решения задачи можно непосредственно воспользоваться со- отношениями (3.69), (3.70) и представить их в виде
m 1+ m 2 m 1 + m 2 Учитывая, что по условию задачи m 2 v 2 = – m 1 v 1, равенство (3) при- нимает вид
= - v. (4) m 1 + m 2 Аналогично получим скорость второго тела u 2 = – v 2. (5) Согласно последним соотноше- до удара
m 1 m 2 ниям сталкивающиеся шары с им- пульсом до удара равным нулю, т. е. m 1 v 1 + m 2 v 2 = 0, после центрального и абсолютно упругого удара шары
m 1 после удара –v 2 меняют направление движения на противоположное без изменения модулей скорости (см. рис.).
Задача 3.19 Найти скорости u 1 и u 2 двух шаров массами m 1 и m 2 после цен- трального и абсолютно упругого удара, если до удара скорость пер- вого шара v 1, а второй шар покоится v 2 = 0. Исследуйте характер дви- жения шаров после удара. Дано: m 1; m 2; v 1; v 2 = 0. Найти: u 1, u 2. Для решения задачи воспользуемся соотношениями (3.69), (3.70). Полагая в них v 2 = 0, имеем
2 m 1 v.
Движение шаров после столкновения зависит от соотношения ме- жду их массами. Действительно: а) если m 1 > m 2, то u 1 > 0, u 2 > 0, т. е. направления движения обоих тел после столкновения совпадают с направлением движения первого тела до столкновения. При этом
скорость первого тела уменьшается, а скорость второго превосходит его ско- рость до удара (см. рис. 1); б) если m 1 = m 2, то u 1 = 0, u 2 = v 1.
до удара
v 1 Рис. 1
< u 2 в) если m 1 < m 2, то до удара u 1 < 0, u 2 > 0. Из этих неравенств следует, что первое тело после столкнове- ния изменяет направление движе- ния на противополож-
после удара
ное и движется с мень- шей скоростью, чем до удара. Скорость второго шара при этом совпадает по направлению со ско- ростью первого до удара, до удара
после удара
m 1
2 m 1 v.
Задача 3.20 m 1 + m 2 m 1 + m 2 Найти скорость u 1 шара массой m 1 после центрального и абсолют- но упругого удара о неподвижный второй шар, если до удара ско- рость первого шара v 1и масса второго шара значительно превыша- ет массу первого, т. е. m 2» m 1. Исследуйте характер движения ша- ров после удара. Дано: m 1; v 1; m 2» m 1. Найти: u 1.
u = m 2 v
» ⎛ m 1 - ⎞ v; u =
2 m 1 m 2 v» 2 m 1 v.
1 1
m 1 +1 2 m 2 Отсюда следует, что первое тело отскакивает от значительно боль- шего по массе шара, слегка меняя скорость по модулю. Второе же после удара движется в направлении первого до удара с очень ма- лой скоростью. В пределе m 2 ® ¥ первое тело меняет направление на противоположное без изменения модуля, а второе остается не- подвижным. u 1 = – v 1; u 2 = 0.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 503; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.73.125 (0.409 с.) |

 dt å mivi = åå Fik = å(Fi 1+ Fi 2+... + Fii -1+ Fii +1+ Fin). (3.54)
dt å mivi = åå Fik = å(Fi 1+ Fi 2+... + Fii -1+ Fii +1+ Fin). (3.54) dt ⎜⎝å mivi ⎟⎠ = 0 ® å mivi = const. (3.58)
dt ⎜⎝å mivi ⎟⎠ = 0 ® å mivi = const. (3.58)
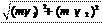

 tga = m 1 v 1, ® a = arctg m 1 v 1,
tga = m 1 v 1, ® a = arctg m 1 v 1, Численные значения параметров представлены в ответе.
Численные значения параметров представлены в ответе.
 u = m 1 v 1 + m 2 v 2. (3.64)
u = m 1 v 1 + m 2 v 2. (3.64)


 2(m 1 + m 2)
2(m 1 + m 2)




 Ä K = K - K =
Ä K = K - K =
 2(m 1 + m 2)
2(m 1 + m 2) ра, скорость v образовавшего- ся тела (пуля + шар) после уда- ра и количество Q выделившего- ся тепла.
ра, скорость v образовавшего- ся тела (пуля + шар) после уда- ра и количество Q выделившего- ся тепла.
 (m M) gh
(m M) gh Q = 0 -
Q = 0 -
 Из уравнения (2), с учетом (3), получим
Из уравнения (2), с учетом (3), получим v = =
v = = Подставляя (6) в (5), найдем выражение для скорости пули до столкновения
Подставляя (6) в (5), найдем выражение для скорости пули до столкновения
 2
2



 установим, что большая часть (> 94 %) первоначальной кинетической энергии пули при столкновении тел тратится на образование тепла.
установим, что большая часть (> 94 %) первоначальной кинетической энергии пули при столкновении тел тратится на образование тепла. Ответ: v = =
Ответ: v = = v = ⎛ M + 1⎞
v = ⎛ M + 1⎞ Q = M (M + m) gL (1- cos a)
Q = M (M + m) gL (1- cos a)
 m 1 u 1 + m 2 u 2 = m 1 v 1 + m 2 v 2; (3.67)
m 1 u 1 + m 2 u 2 = m 1 v 1 + m 2 v 2; (3.67) 1;
1; m 1 v 1 + m 2 v 2;
m 1 v 1 + m 2 v 2;
 = -(m 1 - m 2) v 1 - 2 m 2 v 2;
= -(m 1 - m 2) v 1 - 2 m 2 v 2; Ä = m 1;
Ä = m 1;


 v 1 v 2
v 1 v 2 –v 1
–v 1 Ответ: u 1 = – v 1; u 2 = – v 2.
Ответ: u 1 = – v 1; u 2 = – v 2. Последние соотношения означают, что после столкновения первое тело останавливается, а второе движется со скоростью первого и в его направлении до удара. Иначе говоря, при столкнове- нии шаров происходит обмен ско- ростями между ними (рис. 2);
Последние соотношения означают, что после столкновения первое тело останавливается, а второе движется со скоростью первого и в его направлении до удара. Иначе говоря, при столкнове- нии шаров происходит обмен ско- ростями между ними (рис. 2);


 после удара
после удара



 Рис. 2
Рис. 2 u 1
u 1 Рис. 3
Рис. 3 Полагая v 2 = 0 в формулах (3.69), (3.70), представим результат в виде
Полагая v 2 = 0 в формулах (3.69), (3.70), представим результат в виде m 1 -1
m 1 -1



 Такой же результат получается при упругом столкновении шара со стеной при его нормальном падении на стену (рис.).
Такой же результат получается при упругом столкновении шара со стеной при его нормальном падении на стену (рис.).


