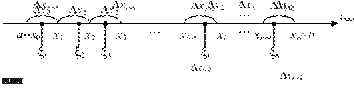Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Физический смысл производной
Понятие производной введено Г. Лейбницем (Германия) и И. Нью- тоном (Великобритания) в конце XVII века практически одновремен- но. Лейбниц решал геометрическую задачу о проведении касатель- ной к плоской кривой. Ньютон же рассматривал движение точки и ввел понятие скорости в данный момент времени. Так как значение производной от функции в данной точке характеризует скорость изме- нения функции в этой точке по сравнению со скоростью возраста- ния независимой переменной, можно использовать понятие произ- водной при определении скорости различных процессов. Замечания 1. Для независимой переменной x по определению dx = Ä x. 2. dx 3. В физике для производной по времени приняты следующие обозначения:
dt ТАБЛИЦА ПРОИЗВОДНЫХ И ОСНОВНЫЕ ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ Для нахождения производных пользуются таблицей производных элементарных функций.
(C)¢ = 0 (2.12) (u + v)¢ = u ¢ + v ¢ (2.13) (Cu)¢ = Cu ¢ (2.14) (uv)¢ = u ¢ v + uv ¢ (2.15) ⎛ u ⎞ ¢=⎛ u ¢ v - uv ¢ ⎞ ⎜⎝ v ⎟⎠ ⎜⎝ v 2 ⎟⎠ (2.16)
Приведем примеры нахождения производных. Пример 1. Найти производную от функции y = 5 x 3 - 2 x 2 + 3 x - 4. Основываясь на формуле (2.13), имеем y ¢= (5 x 3)¢- (2 x 2)¢+ (3 x)¢- (4)¢. Далее, применяя формулы (2.12) и (2.14), получаем y ¢= 5(x 3)¢- 2 (x 2)¢+ 3(x)¢.
Наконец, пользуясь формулой (3) из таблицы, приходим к окон- чательному результату y ¢= 5 × 3 x 2 - 2 × 2 x + 3×1, или y ¢= 15 x 2 - 4 x + 3.
Пример 2. Дано: y = x 3 cos x. Найти: y ¢. По правилу дифференцирования произведения функций (2.15) получаем y ¢= x 3 (-sin x) +3 x 2 cos x, или y ¢=- x 3 sin x +3 x 2 cos x. Здесь применялись формулы (3) и (14) из таблицы.
ПРОИЗВОДНЫЕ СЛОЖНЫХ ФУНКЦИЙ
например, как y (t) = или y (t) = 3 cos2p t. В подобных случа- ях пользуются более общими формулами дифференцирования, осно- ванными на теореме о производной функции от функции. Пусть y есть функция от u: y = f (u), где u в свою очередь функция от аргумента x: u = j(x); в таком случае говорят, что y есть функция от функции. Очевидно, можно записать y = f (j(x)). Если существу- ютпроизводные fu ¢= f ¢(u) и ux ¢=j¢(x),тосуществуетипроизвод- ная от y по x, причем имеет место равенство y ¢= fu ¢× ux ¢. (2.17) Индексы указывают, по какой переменной производится диффе- ренцирование. Покажем, как пользоваться формулой (2.17). Пример 1. Найти y ¢, если y = (x 2+ 5 x + 7)8. Полагая u = x 2+5 x +7,имеем y = u 8.По формуле (3) y ¢=8 u 7 (2 x +5), или, окончательно y ¢= 8(x 2+ 5 x + 7)7(2 x + 5). Пример 2. Найти y ¢, если y = ln (x 3 + 7 x + 2). Принимая в данном случае за u = x 3 + 7 x + 2 и пользуясь форму- лой (10), получаем y ¢= 3 x 2 + 7
x 3 + 7 x + 2
Многие физические величины определяются как производные по времени от других физических величин. Например, скорость � — � v первая производная радиус-вектора r по времени t. Обозначается это следующим образом: � v � = dr или �= �¢= �.. (2.18)
Ускорение � — первая производная скорости � по времени t
a = dv v или �= �¢= �.. (2.19)
Сила тока I — первая производная заряда q по времени t (или, что то же самое, скорость изменения заряда)
dt или I = qt ¢= q.. (2.20) Электродвижущая сила индукции e — взятая со знаком «минус» пер- вая производная магнитного потока Ф по времени
e = - dФ илиe=– Ф ¢=- Ф ·. (2.21) dt t Вопросы и задания для самопроверки
1. Дайте определение дифференциала функции в точке. 2. Дайте определение производной функции. 3. Поясните геометрический смысл производной и дифферен- циала. 4. Поясните механический смысл производной. 5. Пользуясь таблицей производных и основными правилами диф- ференцирования (формулами 2.12–2.19), найдите производные от следующих функций: 1) y = 9 x 2 - 2 x + 3, 2) y = 6 x 3 + 3 x - 4, 3) y = 5 x + ln x + 3sin x, 4) y = 7 ln x 3- 2 cos x, 5) y = x 3 ln x, 6) y = x 2 sin x, 7) y = tgx 3 cos x,
9) y = 3 × cos 2p x. 6. Приведите примеры физических величин, которые являются производными от других физических величин по времени.
Примеры решения задач Задача 2.1 Радиус-век�тор материал�ьной точки меняется со временем по зако- � � ну r (t) = 2 t 2 i + 3 t j + 4 k, м. Найти: 1) зависимость скорости точ- ки от времени � (t), 2) зависимость модуля скорости от времени v (t), v � 3) зависимость ускорения точки от времени a (t), 4) зависимость мо- дуля ускорения от времени a (t), 5) значения скорости и ускорения в момент времени t =�1 с от начал�а движения. � � Дано: r (t) = 2 t 2 i + 3 t j + 4 k, м; t = 1 c. Найти: � (t), v (t), �(), a (t), v, a. v � a t � 1. Скорость v — первая производная радиус-вектора r по време- ни. Поэтому для нахождения зависимости � (t) достаточно продиф- v � � ференцировать по времени заданную зависимость r = r (t):
dt t 2. Модуль вектора определяется по теореме Пифагора как корень из суммы квадратов компонент вектора. Для модуля скорости
Из уравнения (1) имеем vx = 4 t м/c, vy = 3 м/c, vz = 0 м/c. Получаем
3. Так как ускорением � является первая производная скорости � a � v
(t) — выражение (1). Тогда � � dv � � ×¢ � � �
4. Как видно из зависимости (3), ax = 4 м/c2, ay = 0 м/c2, az = 0 м/c2. По- этому
5. Значения скорости и ускорения в момент времени t = 1 с от на- чала движения легко получить, подставив значение времени t = 1 с в выражения (2) и (4). Тогда v (1) = 5 м/c, a (1) = 4 м/c2. � �
зависимость модуля скорости от времени v (t) =� , м/с; за-
Задача 2.2 Заряд на обкладках конденсатора меняется согласно уравнению q (t) = 0,03 × cos2p t, Кл. Найти силу тока I в цепи в момент времени t = 6 с. Дано: q (t) = 0,03 × cos2p t, Кл; t = 6 с. Найти: I (6). Сила тока I — это первая производная заряда q по времени t. Ис- ходя из этого определения, получим зависимость тока в цепи от вре- мени I (t). Для этого продифференцируем заданную зависимость q (t) по времени.
dt t (здесь А — Ампер, единица измерения силы тока). Теперь в полученное выражение подставим значение времени t = 6 с. I (6) = -0,03× 2p×sin 2p× 6 = -0,03× 2p×sin12p = 0 A.
(так как sin12p = sin0 = 0) Ответ: I (6) = 0 А.
Задача 2.3 Магнитный поток Ф, пронизывающий рамку, меняется со време- нем по закону Ф (t) = 4 × sin p t, Вб. Найти модуль эдс индукции e, воз- никающей в рамке в момент времени t = 8 с. Дано: Ф (t) = 4 × sin p t, Вб; t = 8 с. Найти: Ф (8). 2 Согласно закону электромагнитной индукции эдс, возникающая в рамке, определяется выражением
dt Поэтому сначала найдем зависимость эдс от времени, дифферен- цируя по времени заданную зависимость Ф (t)
p ⎞×¢
t = -4 × p × cos p t, В 2 2 В полученную зависимость e(t) подставляем t = 8 с и получаем e(8) =-2p×cos ⎛ p ×8⎞= -2p×cos (4p) = -2p×1 = -6,28 В. ⎜⎝ 2 ⎟⎠ Ответ: модуль эдс индукции e (8) = 6,28 В.
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ПЕРВООБРАЗНАЯ ФУНКЦИЯ Первообразной функцией (или просто первообразной) для данной функции одной переменной y = f (x) называется такая функция F (x), производная от которой равна f (x) (или, что то же самое, дифферен- циал от которой равен f (x) dx): F ¢(x) = f (x) или dF (x) = f (x) dx. (3.1) Первообразных функций для данной — бесконечное множество; разность между двумя первообразными функциями F 1 (x) и F 2 (x) — ве-
Рис. 3.1 НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
всех первообразных функций от данной функции f (x) называется неопределенным интегралом от функции f (x) или от дифференциала f (x) dx. Обозначение: F (x) + const = ò f (x) dx. (3.2) (ò — знак интеграла, f (x) — подынтегральная функция, f (x) dx — по- дынтегральное выражение).
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ Определенным интегралом функции y = f (x) в пределах от а до b, заданной в замкнутом интервале [ а, b ] (при этом может быть а < b (случай А) или а > b (случай Б)), называется число, получаемое сле- дующим образом: 1) интервал [ а, b ] разбивается на n «элементарных интервалов» произвольными числами x 1, x 2, …, x n –1, выбранными так, что a = x0 <x1 <x2 <… <xi <…<xn-1 <xn = b или a = x0 > x1 > x2 >… > xi >…> xn-1 > xn = b. 2) внутри (или на границе) каждого элементарного интервала [ xi –1, xi ] выбирается произвольно одно число x I (рис. 3.2):
xi –1 £ x I £ xi или xi –1 ³ x I ³ xi;
3) значения f (x i) функции y = f (x) в этих выбранных точках умно- жаются на соответствующие разности Ä xi –1 = xi — xi –1 (длины элемен- тарных интервалов [ xi –1, xi ], взятые со знаками «+» или знаками «-»); 4)
все полученные n произведений f (x i) × Ä xi –1 складываются;
Рис. 3.2
5) вычисляется предел полученной суммы
å f (x i) × Ä xi -1, когда i =1 длина каждого элементарного интервала Ä xi –1 стремится к нулю (и, следовательно, n ® ¥). Если этот предел существует и не зависит от выбора чисел xi и xI, то он называется определенным интегралом b n ò f (x) dx = lim å f (x i) × Ä xi -1 (3.3)
a n ®¥ Символ ò называется знаком интеграла, число a — нижним преде- лом, число b — верхним пределом, функция f (x) — подынтегральной функцией, выражение f (x) dx — подынтегральным выражением, буква x — переменной интегрирования. Значение интеграла зависит только от вида функции f (x) и от пределов a и b, но не зависит от перемен- ной интегрирования, которая может быть обозначена любой буквой. b b b Так ò f (x) dx = ò f (y) dy = ò f (z) dz и т. п. a a a
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 680; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.205.146 (0.132 с.) |
 Наряду с обозначением y ¢ используют запись y ¢= dy.
Наряду с обозначением y ¢ используют запись y ¢= dy. x = x (t); x. = dx.
x = x (t); x. = dx.



 Таблица производных элементарных функций
Таблица производных элементарных функций x
x



 Продолжение табл.
Продолжение табл. xn
xn
 cos2 x
cos2 x
 1+ x 2
1+ x 2
 x
x

 Существуют следующие основные правила дифференцирова- ния (здесь С — постоянная, а u и v — функции от x, имеющие про- изводные):
Существуют следующие основные правила дифференцирова- ния (здесь С — постоянная, а u и v — функции от x, имеющие про- изводные): Приведенные в предыдущем параграфе правила и формулы диф- ференцирования позволяют находить производные от функций толь- ко в самых простых случаях. Знания этих правил и формул недоста- точно для дифференцирования функций более сложного вида, таких,
Приведенные в предыдущем параграфе правила и формулы диф- ференцирования позволяют находить производные от функций толь- ко в самых простых случаях. Знания этих правил и формул недоста- точно для дифференцирования функций более сложного вида, таких, .
. dt v rt r
dt v rt r dt a vt v
dt a vt v I = dq
I = dq
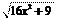 8) y =,
8) y =,
 v =.
v =.
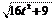 v (t) = =, м/с (2)
v (t) = =, м/с (2) a = dt = (4 ti + 3 j) t = 4 i + 0 j = 4 i, м/с. (3)
a = dt = (4 ti + 3 j) t = 4 i + 0 j = 4 i, м/с. (3)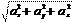 Модуль ускорения определяется соотношением a =.
Модуль ускорения определяется соотношением a =. a = = 4 м/с2. (4)
a = = 4 м/с2. (4)
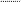
 личина постоянная. Графики всех функ- ций F 1 (x), F 2 (x), F 3 (x), …, первообраз- ных для данной, представляют собой одну и ту же кривую и получаются один из другого в результате параллельного сдвига кривой в направлении оси орди- нат в ту или иную сторону (рис. 3.1).
личина постоянная. Графики всех функ- ций F 1 (x), F 2 (x), F 3 (x), …, первообраз- ных для данной, представляют собой одну и ту же кривую и получаются один из другого в результате параллельного сдвига кривой в направлении оси орди- нат в ту или иную сторону (рис. 3.1).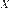 Общее выражение F (x) + const для
Общее выражение F (x) + const для