Плоское движение твердого тела

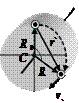
Плоским движением называется такое движение, при котором все точки абсолютно твердого тела движутся параллельно одной плос- кости. Например, при качении цилиндра (колеса) по горизонталь- ной поверхности все точки движутся в плоскости XOY, перпендику- лярной поверхности (рис. 5.7). Рассмотрим движение произвольной точки А при ее перемещении вместе с цилиндром из положения 1 в положение 3. Представим сложное движение любой точки цилин- дра (траектория такого дви жения называется циклоида) как сумму двух простых движений: поступательного движения из положения 1 в положение 2 относительно неподвижной системы ко ординат K и вращательного движения из положения 2 в положение 3 (поворот на угол j вокруг оси, проходящей через центр масс системы точку С) относительно движущейся системы кординат K ¢, жестко связанной с центром масс системы. Выберем за начало инерциальной системы отсчета К неподвижную точку О, совпадающую в начальный момент с центром масс системы точкой С.

о

K y

x а

z

K `

z ` x ` б

Рис. 5.7

� � �

В неподвижной системе координат K (рис. 5.7а) имеем равенство

r = r 0 + r ¢,

где вектор � — перемещение точки А из начального в конечное. Век-

� r

тор r 0 — перемещение в этой же системе отсчета за это же время точ-

5.7. Плоское движение твердого тела 313

 

ки А, совершающей поступательное движение из начального поло- жения в промежуточное. Отметим, что центр масс тела точка С при движении цилиндра совершает только поступательное перемеще- ние. Из (рис. 5.7а) следует, что поступательное движение т. А совпа-

r

дает с движением точки С. Вектор �¢ — перемещение в системе от-

счета К т. А из промежуточного положения в конечное. Последнее перемещение можно представить (рис. 5.7б) как вращение вокруг неподвижной оси в системе отсчета K ¢, жестко связанной с движу-

�

щимс�я ц�ентром масс системы (т. С). В этой системе отсчета вектор

r ¢ = R - R 0�. Продифференцируем указанное выше векторное равен-

ство для r по времени

� � �

¢

dr = dr 0 + dr. (5.50)

По определению

dt dt dt

� �

� dr � dr 0

v =

� dt

и v 0 = dt.

Так как R 0 не меняется со временем, то

� � � �

dr ¢ = dR - dR 0 = dR =�,

v dt dt dt dt л

� � �

и

w Ц

vл

vл = [w Ц, R ],

где

� � — линейная и угловая скорости вращательного движе-

ния вокруг неподвижной оси, проходящей через центр масс. Таким образом, имеем

� � �

v = v 0 + [w Ц, R ]. (5.51)

Так как при поступательном движении все точки тела движутся одинаково, то

� 1 � 1 � m � �

vC = m å miv 0 i = m (å mi) v 0 = m v 0 = v 0

i i

и � � �

v = vС + [w Ц, R ]. (5.52)

Таким образом, плоское движение твердого тела можно предста- вить как сумму поступательного движения его центра масс и враща- тельного движения относительно неподвижной оси, проходящей че- рез центр масс.

 

В общем случае скорость твердого тела при плоском движении мож- но представить как векторную сумму скоростей поступательного дви- жения любой его точки (не обязательно центра масс) и вращательно- го движения, обусловленного вращением вокруг оси, проходящей через эту точку.

Если представлять плоское движение твердого тела через движение его центра масс, то система уравнений (5.1) и (5.27) сводится к виду

� �

maC = F, (5.53)

IC e Цz = MЦz. (5.54)

Здесь IC — момент инерции тела относительно оси, проходящей через его центр масс. Переменные в первом уравнении рассчитыва- ются относительно инерциальной системы отсчета, а во втором — относительно системы, связанной с центром масс (инерции), т. е. в Ц-системе.