Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Релятивистское уравнение движения.Содержание книги
Поиск на нашем сайте
Релятивистское уравнение движения по внешнему виду совпадает с записью основного закона динамики Ньютона в общей формулировке:
Лишь в двух случаях, когда сила нормальна к вектору скорости или сонаправлена с ним, ускорение и сила по направление совпадают. Силы инерции. Как уже отмечалось, существуют такие системы отсчета, в которых ускорение тел вызывается не только действием сил, но и самим движением системы отсчета. Рассмотрим поведение свободного тела, находящегося в покое относительно неподвижной системы. В этой системе выполняются законы Ньютона: равнодействующая приложенных к телу сил равна нулю и тело, как следствие, находится в покое. Если же другая система отсчета движется относительно первой с ускорением a, то в подвижной системе тело получает ускорение - а, равное по величине ускорению системы и противоположно ему направленное. Следовательно, в подвижной системе законы Ньютона не выполняются: равнодействующая приложенных сил равна нулю, а тело приобретает ускорение.
объясняющая появление ускорения тепа в подвижной системе отсчета. Т.е. сила инерции равна произведению массы тела на ускорение системы и противоположно ему направлена. Если связать систему отсчета с ускоренно движущимся телом, то геометрическая сумма всех сил, приложенных к телу, включая силу инерции, равна нулю (принцип Даламбера) Силы инерции во вращающихся системах отсчета.
Такую силу называют центробежной силой. Силы инерции Кориолиса.
Абсолютный импульс тела определяется относительным и переносным движением
Со временем будут изменяться обе составляющие абсолютного импульса. Рассмотрим сначала изменение относительного импульса. Поскольку тело движется равномерно относительно подвижной системы, будет изменяться только направление импульса. За промежуток времени система (и ее радиус) поворачивается на угол Dj = wDt (рис. 37).
 При малых углах поворота вращение относительного импульса равно: При малых углах поворота вращение относительного импульса равно:
Изменение величины переносного импульса за время dt равно
С другой стороны, из основного закона динамики следует: где F - равнодействующая приложенных к телу сил.

Учитывая направления (рис. 39) векторов в векторном виде можно записать
В системе, связанной с вращающимся стержнем, тело движется равномерно и прямолинейно, т.е. сумма приложенных к нему сил должна быть равной нулю. Как видно из рисунка, в горизонтальной плоскости силы не уравновешены, поэтому необходимо для выполнения законов динамики ввести силы инерции (на рисунке показаны пунктиром). Вдоль стержня действует центробежная сила инерции, уравновешивающая центростремительную силу.
Как видно из, сила Кориолиса возникает во вращающейся системе отсчета при относительном движении тел. Силы трения. Сухое трение.
Сухим (внешним) трением называют силы сопротивления движению, возникающие при относительном движении одного твердого тела по поверхности другого. Силы сопротивления движению определяются наличием микро- и макронеровностей поверхностей трущихся тел и взаимодействием между ними. При скольжении одной твердой поверхности по другой в плоскости соприкосновения тел возникают силы, направленные противоположно относительной скорости. Эти силы и называют силами трения скольжения. Коэффициент трения скольжения k является безразмерной величиной и определяется природой и состоянием поверхностей трущихся тел. Кроме закона Кулона опытным путем установлен ряд закономерностей для трения скольжения среди которых наиболее часто употребляются следующие: 1. При попытке сдвинуть одно тело по поверхности другого в плоскости контакта возникают силы, сопротивления, изменяющиеся от нуля до предельного значения, называемого силой трения покоя. 2. С увеличением относительной скорости трущихся тел силы - трения сначала убывает, а затем начинают возрастать. 3. Силы трения тем меньше, чем тверже трущиеся поверхности. Силы трения качения.
Сопротивление качению может возникать в том случае, если нормальная реакция смещается относительно вертикального диаметра катка в сторону движения. Это происходит в том случае, если давление катка на поверхность будет не в точке, а по участку поверхности, а интенсивность давления будет больше впереди вертикального диаметра катка, как показано на рис. 44.
Следовательно, поверхность должна деформироваться, причем деформации будут несимметричными относительно вертикального диаметра. Положим, что сила Здесь Вязкое трение Вязкое трение возникает при относительном движении слоёв жидкости или газа. Основные законы вязкого трения получены опытным путём. Ньютон установил, что если под действием силы площадка На подвижную площадку действуют силы сопротивления движению (силы вязкого трения): где При движении тел в вязкой среде на них действуют силы сопротивления движению. Стокс получил выражение для этих сил. При малых скоростях.
где:
Движение тел в сопротивляющейся среде. При достаточно больших скоростях тел (или если форма тела является плохо обтекаемой) силы Стокса становятся пропорциональны квадрату скорсти: Положим, что тело начинает падать под действием силы тяжести в сопротивляющейся среде. Пренебрегая силой Архимеда, запишем: С течением времени скорость тела возрастает, возрастает и сила Стокса. Наконец, силы тяжести и Стокса уравновешиваются, после чего начинается равномерное движение тела с установившейся скоростью Обозначим:
Интегрируя, получим: Константу интегрирования находим из начальных условий (x=0 и Подставив (197) в (196) получим: Через достаточно большой промежуток времени (
Упругие силы. Упругостью называют свойство восстанавливать времменно утраченную форму и объём, а деформациями- само изменение формы и объёма тела. Причиной упругости является наличие одновременно присутствующих сил взаимодействия между частицами тела- притяжения ( На рис.46 представлены графики силы взаимного отталкивания (1), притяжения (2) и равнодействующая этих сил (3). На расстоянии Потенциальная энергия взаимодействия на расстоянии
, Графики потенциальной энергии сил отталкивания (1), притяжения (2) и равнодействующей (3) представлены на рис.47:
|
||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 772; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.63.214 (0.009 с.) |


 Релятивистское уравнение динамики удовлетворяет преобразованиям Лоренца и, следовательно, общефизическому принципу относительности. Важно отметить, что в отличие от классического закона динамики в релятивистском случае сила и ускорение могут не совпадать по направлению:
Релятивистское уравнение динамики удовлетворяет преобразованиям Лоренца и, следовательно, общефизическому принципу относительности. Важно отметить, что в отличие от классического закона динамики в релятивистском случае сила и ускорение могут не совпадать по направлению: Чтобы и в таких системах выполнялись законы Ньютона, приходится вводить дополнительные фиктивные силы, называемые силами инерции. В рассмотренном примере в подвижной системе вводится сила инерции:
Чтобы и в таких системах выполнялись законы Ньютона, приходится вводить дополнительные фиктивные силы, называемые силами инерции. В рассмотренном примере в подвижной системе вводится сила инерции:
 Пусть система вращается равномерно с угловой скоростью ω. Вдоль радиуса системы равномерно со скоростью v движется тело (рис. 36).
Пусть система вращается равномерно с угловой скоростью ω. Вдоль радиуса системы равномерно со скоростью v движется тело (рис. 36).


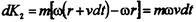
 полное изменение импульса тела равно
полное изменение импульса тела равно
 Таким образом, наблюдаемые изменения импульса вызываются внешними силами, равными по величине: F=2mnw
Таким образом, наблюдаемые изменения импульса вызываются внешними силами, равными по величине: F=2mnw






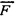
 Силу уравновешивает сила инерции Кориолиса:
Силу уравновешивает сила инерции Кориолиса:
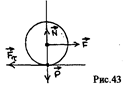 Трение качения возникает при качении одного твердого тела по поверхности другого. При попытке сдвинуть тело по поверхности другого в плоскости соприкосновения возникает
Трение качения возникает при качении одного твердого тела по поверхности другого. При попытке сдвинуть тело по поверхности другого в плоскости соприкосновения возникает сила препятствующая этому.
сила препятствующая этому.
 вызывает равномерное качение катка, т.е.
вызывает равномерное качение катка, т.е. 

 (коэффициент трения качения) является размерной величиной. Смысл его- ''плечо'' нормальной составляющей реакции поверхности.
(коэффициент трения качения) является размерной величиной. Смысл его- ''плечо'' нормальной составляющей реакции поверхности. площади
площади 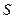 движется равномерно со скоростью
движется равномерно со скоростью  относительно площадки
относительно площадки  ,
, 

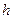 - расстояние между площадками (слоями),
- расстояние между площадками (слоями),  - коэффициент вязкого трения определяемая свойствами вязкой среды, заполняющей промежуток между площадками.
- коэффициент вязкого трения определяемая свойствами вязкой среды, заполняющей промежуток между площадками.
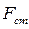 - стоксова сила сопративления,
- стоксова сила сопративления,  - плотность среды,
- плотность среды,  -коэффициент, определяемый геометрией тела,
-коэффициент, определяемый геометрией тела, 


 . Определим зависимость скорости от проходимого телом пути и значение установившейся скорости.
. Определим зависимость скорости от проходимого телом пути и значение установившейся скорости. 

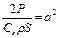
 Или
Или 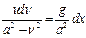


 или
или 

 ) скорость тела перестаёт изменяться. Следовательно, значение установившейся скорости равно
) скорость тела перестаёт изменяться. Следовательно, значение установившейся скорости равно 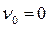 .
.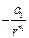 ) и отталкивания (
) и отталкивания ( ). Равнодействующая этих сил равна:
). Равнодействующая этих сил равна: 
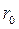 между взаимодействующими частицами равнодействующая равна нулю (положение равновесия). При
между взаимодействующими частицами равнодействующая равна нулю (положение равновесия). При  <
<  где:
где: 
 .
.