
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Продольные волны в твёрдом теле. Волновое уравнение.Содержание книги
Поиск на нашем сайте
По второму закону динамики
Переходя к пределу при Δx→ 0, получаем уравнение:
Это и есть волновое уравнение. Из него видно, что смещение частиц среды может распространяться вдоль стержня в виде упругих волн ξ = a sin(ωt - kx) или ξ = a sin(ωt + kx). Уравнению (423) будет также удовлетворять и суперпозиция таких волн. Уравнение плоской волны, полученное ранее, является решением волнового уравнения. Таким образом, волновому уравнению (423) удовлетворяют синусоидальные волны. Более того, если волновому уравнению удовлетворяют синусоидальные волны различных частот, то и их суперпозиция также удовлетворяет волновому уравнению, т.е. косинусоидальная волна также может рассматриваться как решение приведенного волнового уравнения. Рассматривая аналогичным образом волну, движущуюся в произвольном направлении в пространстве, можно получить волновое уравнение в виде:
Упругие волны в газах. Волновое уравнение. Для вывода волнового уравнения для газов выделим цилиндрический столб газа сечения S 0, и длины Δx При распространении в столбе продольной звуковой волны граничные сечения испытывают смещения от первоначального положения. Смещение левого сечения равно ξx, а правого - ξx+Δx.
Разность сил давления, действующих на столб газа в направлении распространения волны, равна:.
Решением волнового уравнения является уравнение плоской волны:
Учитывая, что:
получаем после подстановки этих значений в волновое уравнение:
Скорость волны в газах, как видим, не зависит от давления, а определяется родом газа (значениями γ и μ) и его температурой Т. Если рассмотреть подобным образом распространение волны в произвольном направлении в пространстве, уравнение волны получим в виде:
где: kx,ky,kz - проекции волнового вектора на оси координат. Интерференция воли. Особый интерес представляет тот случай, когда частоты колебаний источников одинаковы, одинаковы и направления колебаний, что касается фаз колебаний источников, то они могут быть одинаковы, иди разность фаз не изменяется со временем. Такие источники называются когерентными. Для когерентных источников картина сложения волн (интерференционная картина) является устойчивой. Результирующее колебание в любой точке среды имеет постоянную амплитуду колебаний, зависящую от расстояния точки среды от источников волн (так называемой разности хода).
Для получения интерференционной картины удобно воспользоваться источниками сферических волн. Далее будем рассматривать интерференцию от достаточно удаленных источников сферических волн. Сами же источники находятся на относительно близком расстоянии друг от друга. При таких предположениях амплитуды волн, приходящих от источников в выделенный участок среды, можно считать одинаковыми и в пределах этого участка - не зависящими от расстояний от источника.
По принципу суперпозиции результирующее смещение частиц в этой точке равно:
Условие максимума амплитуды колебаний в точке среды имеет вид:
где п = 1,2,3,..., откуда максимум амплитуды колебаний имеет место при разности хода, равной: т.е. максимум амплитуды получается в точках, для которых разность хода равна нулю или целому числу волн.
т.е. разность хода для этого случая должна быть равной: где и =1,2,3,... Следовательно, минимум амплитуды колебаний получается в точках, для которых разность хода равна нечётному числу полуволн. Таким образом, в результате сложения двух волн в среде возникают колебания, амплитуда которых в общем случае различна для различных точек среды и определяется разностью хода. В результате чередования в пространстве интерференционных максимумов и минимумов возникает интерференционная картина. Картина неподвижна, хотя и образуется бегущими волнами Стоячие волны. В качестве примера интерференции двух волн могут служить так называемые стоячие волны - результат суперпозиции двух волн одинаковой амплитуды, движущихся во встречных направлениях.
Как видно, результирующее колебание происходит с той же частотой, с какой частицы среды колеблются в прямой и встречной волне. Амплитуда колебаний зависит от положения точки среды (координаты х), но для одной и той же точки остаётся постоянной с течением времени. Такую периодическую во времени и в пространстве картину называют стоячей волной, которая описывается уравнением стоячей волны.
Вид этих зависимостей, аналогичный уравнению стоячей волны для смещений, позволяет сделать заключение, что скорости и ускорения колебаний частиц около их положений равновесия также образуют стоячие волны.
Относительную деформацию участка среды, в котором установилась стоячая волна, также легко определить из уравнения стоячей волны:
момента времени отвечает условие, где n - целое число. Из этого условия координаты пучностей стоячей волны равны:
Сравнивая уравнения стоячей волны (431), (432) и (433) для смещений, скоростей и ускорений, заметим, что фаза ускорения от скорости и фаза скорости от смещения
смещений и наоборот. Поскольку для узлов смещений относительная деформация принимает максимальные значения, в этих точках будут максимальными и упругие напряжения (силы). На практике стоячие волны получают в результате наложения бегущей волны и волны, отраженной от границы раздела сред. В зависимости от условий на границе раздела стоячая волна принимает тот или иной вид. Например, стоячая волна образуется в результате сложения бегущей волны с отраженной от более плотной среды. Как было получено в 17.7., от более плотной среды происходит антифазное отражение, амплитуда отраженной волны изменяет свой знак на противоположный. Так как фаза меняется на противоположную на расстоянии, равном половине длины волны, факт антифазного отражения называют потерей полволны. Вследствие этого результирующее смещение, если пренебречь изменением амплитуды при отражении, в любой момент времени на границе раздела сред равно нулю, т.е. при отражении от более плотной среды на границе раздела сред образуется узел стоячей волны. Если же отражение происходит от менее плотной среды, знак амплитуды отраженной волны тот же, что и у волны, падающей на границу раздела сред. Поэтому на границе раздела сред образуется пучность стоячей волны, амплитуда колебаний частиц в которой равна удвоенной амплитуде падающей волны.
|
||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 365; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.200.56 (0.008 с.) |


 В твёрдом теле, в котором распространяется продольная волна в направлении оси ОХ, выделим стержень сечения S0, ось которого совпадает с направлением распространения волны. В стержне выделим небольшой участок между сечениями, имеющими координаты х и x+Δx (рис.135). При распространении волны стержень деформируется, и координаты граничных сечений выделенного участка изменяются. Пусть к моменту времени t + Δt координата левого сечения участка равна х', тогда смещение этого сечения за промежуток времени Δt равно. Правое граничное сечение участка к моменту времени t + Δt имеет координату
В твёрдом теле, в котором распространяется продольная волна в направлении оси ОХ, выделим стержень сечения S0, ось которого совпадает с направлением распространения волны. В стержне выделим небольшой участок между сечениями, имеющими координаты х и x+Δx (рис.135). При распространении волны стержень деформируется, и координаты граничных сечений выделенного участка изменяются. Пусть к моменту времени t + Δt координата левого сечения участка равна х', тогда смещение этого сечения за промежуток времени Δt равно. Правое граничное сечение участка к моменту времени t + Δt имеет координату
 а его смещение за промежуток времени Δt равно, средняя же относительная деформация, равная отношению удлинения к первоначальной длине
а его смещение за промежуток времени Δt равно, средняя же относительная деформация, равная отношению удлинения к первоначальной длине Истинной относительной деформацией, или относительной деформацией в точке называется предел, к которому стремится значение средней деформации при Δx→ 0,
Истинной относительной деформацией, или относительной деформацией в точке называется предел, к которому стремится значение средней деформации при Δx→ 0,



 которое справедливо для любой точки. Уравнение показывает, что ускорение данной точки среды пропорционально распределению деформации вдоль направления распространения волны. Выражая напряжение из закона Гука через относительную деформацию, получим:
которое справедливо для любой точки. Уравнение показывает, что ускорение данной точки среды пропорционально распределению деформации вдоль направления распространения волны. Выражая напряжение из закона Гука через относительную деформацию, получим:
 Удлинение столба равно разности смещений:
Удлинение столба равно разности смещений: Относительную деформацию объема, выделенного столба газа через удлинение постоянном сечении запишем в виде:
Относительную деформацию объема, выделенного столба газа через удлинение постоянном сечении запишем в виде: Процесс распространения волны протекает настолько быстро, что теплообменом с окружающей средой можно пренебречь, т.е. процесс изменения состояния газа в выделенном столбе можно считать адиабатическим. Адиабатические процессы подчиняются уравнению р-Vγ = С, откуда: dpVγ + γ Vγ-1∙pdV=0. Учитывая это, установим связь между относительной деформацией объёма и относительным изменением давления:
Процесс распространения волны протекает настолько быстро, что теплообменом с окружающей средой можно пренебречь, т.е. процесс изменения состояния газа в выделенном столбе можно считать адиабатическим. Адиабатические процессы подчиняются уравнению р-Vγ = С, откуда: dpVγ + γ Vγ-1∙pdV=0. Учитывая это, установим связь между относительной деформацией объёма и относительным изменением давления:
 На торцы столба газа действуют силы давления. Если давление на левом торце равно px,то на другом торце.
На торцы столба газа действуют силы давления. Если давление на левом торце равно px,то на другом торце. Масса газа может быть выражена соотношением ρ0S0Δx, где ρ0 - плотность в недеформированном столбе длины Δх. По второму закону Ньютона
Масса газа может быть выражена соотношением ρ0S0Δx, где ρ0 - плотность в недеформированном столбе длины Δх. По второму закону Ньютона ξ = a sin(ωt - kx)
ξ = a sin(ωt - kx)

 Очевидно, что равенство выполняется при условии, что:
Очевидно, что равенство выполняется при условии, что: Так как, скорость волны в газе равна:
Так как, скорость волны в газе равна: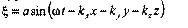

 Рассмотрим результат сложения волн в точке среды, находящейся на расстояниях и
Рассмотрим результат сложения волн в точке среды, находящейся на расстояниях и от источников. Учитывая сказанное выше, уравнения волн в данной точке среды запишем в виде:
от источников. Учитывая сказанное выше, уравнения волн в данной точке среды запишем в виде:
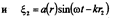

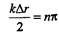 Амплитуда колебаний частиц среды зависит от положения точки в пространстве (от разности хода). В зависимости от разности хода Dr амплитуда колебаний частиц может изменяться от нуля до максимального значения 2a(r).
Амплитуда колебаний частиц среды зависит от положения точки в пространстве (от разности хода). В зависимости от разности хода Dr амплитуда колебаний частиц может изменяться от нуля до максимального значения 2a(r).
 Условие минимума амплитуды определяется следующим равенством:
Условие минимума амплитуды определяется следующим равенством:
 Рассмотрим две плоские волны одинаковой амплитуды, одна из которых распространяется в положительном направлении оси ОХ, а другая - в отрицательном. Соответствующим подбором начала координат и начала отсчёта времени можно добиться того, что в точке пространства с координатой х уравнения этих волн имеют вид:
Рассмотрим две плоские волны одинаковой амплитуды, одна из которых распространяется в положительном направлении оси ОХ, а другая - в отрицательном. Соответствующим подбором начала координат и начала отсчёта времени можно добиться того, что в точке пространства с координатой х уравнения этих волн имеют вид:
 Суперпозиция таких волн даёт результирующее колебание точек среды:
Суперпозиция таких волн даёт результирующее колебание точек среды:
 Из уравнения стоячей волны легко получить зависимости от времени скорости и ускорения колебаний частиц среды около их положений равновесия:
Из уравнения стоячей волны легко получить зависимости от времени скорости и ускорения колебаний частиц среды около их положений равновесия:
 Отметим сначала, что амплитудой колебаний для стоячей волны называют, строго говоря, величину А = |2acoskx|. Поэтому максимуму амплитуды колебаний для любого
Отметим сначала, что амплитудой колебаний для стоячей волны называют, строго говоря, величину А = |2acoskx|. Поэтому максимуму амплитуды колебаний для любого Аналогичным образом определяется условие минимума амплитуды колебаний:
Аналогичным образом определяется условие минимума амплитуды колебаний: откуда координаты узлов стоячей волны равны:
откуда координаты узлов стоячей волны равны: Очевидно, что расстояние между соседними узлами или между соседними пучностями равно половине длины проходящей волны. Расстояние между соседними узлами или между соседними пучностями называется длиной стоячей волны, следовательно, длина стоячей волны связана с длиной проходящей волны соотношением:
Очевидно, что расстояние между соседними узлами или между соседними пучностями равно половине длины проходящей волны. Расстояние между соседними узлами или между соседними пучностями называется длиной стоячей волны, следовательно, длина стоячей волны связана с длиной проходящей волны соотношением: Из уравнения стоячей волны (431) следует, что для любого момента времени частицы среды между соседними узлами имеют смещения одинакового знака. Иначе говоря, эти частицы одновременно проходят положение равновесия и одновременно достигают положений максимального отклонение в одну сторону от положения равновесия. По другую сторону от узла все частицы на расстоянии до следующего узла также одновременно проходят свои положения равновесия и одновременно достигают максимальных отклонений, но уже в другую сторону от положения равновесия. Следовательно, между соседними узлами частицы колеблются в одинаковой фазе, а при переходе через узел фаза колебаний скачком изменяется на.
Из уравнения стоячей волны (431) следует, что для любого момента времени частицы среды между соседними узлами имеют смещения одинакового знака. Иначе говоря, эти частицы одновременно проходят положение равновесия и одновременно достигают положений максимального отклонение в одну сторону от положения равновесия. По другую сторону от узла все частицы на расстоянии до следующего узла также одновременно проходят свои положения равновесия и одновременно достигают максимальных отклонений, но уже в другую сторону от положения равновесия. Следовательно, между соседними узлами частицы колеблются в одинаковой фазе, а при переходе через узел фаза колебаний скачком изменяется на.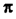 отличаются на. Для них же совпадают узлы и пучности. Что же касается стоячей волны(434) для относительной деформации, то её узлы совпадают с пучностями стоячей волны для
отличаются на. Для них же совпадают узлы и пучности. Что же касается стоячей волны(434) для относительной деформации, то её узлы совпадают с пучностями стоячей волны для


