
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометрическое представление колебаний.Содержание книги
Поиск на нашем сайте
Для более наглядного представления различного рода движений, в том числе и гармонических, применяются графические способы их описания. Среди этих способов мы рассмотрим только самые распространённые. а) Временные диаграммы
Наиболее широко применяемыми и известными являются временные (плоские) диаграммы, на которых в зависимости от времени представляются параметры движения, например, смещение, скорость и ускорение. Если материальная точка совершает движение по гармоническому закону б) векторные диаграммы  и и 
Весьма наглядным является сложение гармонических колебаний, представляемое с помощью векторных диаграмм.
в)Спектральное представление колебаний
В таких случаях на графиках зависимости амплитуды или энергии, пропорциональной амплитуде колебаний, от частоты для соответствующих частот откладываются отрезки, в определенном масштабе равные амплитуде (энергии) колебаний. Спектральная характеристика гармонического колебания частоты w0 представлена на рис. 101. г) Фазовое представление колебаний При фазовом представлении колебаний состояние колеблющейся системы описывается в фазовой плоскости. Фазовой плоскостью называют плоскость, координаты точек которой определяют состояние колеблющейся системы с одной степенью свободы. По осям координат откладываются значения координат и скоростей механической системы. При гармонических колебаниях вместо скорости (или импульса) откладывается обычно отношение скорости тела к циклической частоте колебаний. Рассмотрим фазовые представления некоторых частных случаев движения. На рис. 102 представлено равномерное прямолинейное движение
Если же скорость с течением времени изменяется, то фазовая траектория не будет представлять собой прямую линию. Так, если тело совершает равнозамедленное движение с начальной скоростью  из начала координат, то закон изменения его скорости записывается в виде из начала координат, то закон изменения его скорости записывается в виде  , а закон движения - в форме , а закон движения - в форме  . Исключая из этих зависимостей время, получаем уравнение движения в фазовой плоскости . Исключая из этих зависимостей время, получаем уравнение движения в фазовой плоскости  . Этому уравнению соответствует парабола, представленная на рис.103. . Этому уравнению соответствует парабола, представленная на рис.103.
Этими основными видами геометрического представления колебаний и будем пользоваться в дальнейшем.
|
|||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 295; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.101.7 (0.008 с.) |




 , то скорость её в произвольный момент времени выражается соотношением
, то скорость её в произвольный момент времени выражается соотношением  , а ускорение, соответственно,
, а ускорение, соответственно, 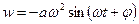 . Временные диаграммы этих параметров отражены на рис.95-97. На рис.98 в произвольном масштабе одновременно представлены все три характеристики движения.
. Временные диаграммы этих параметров отражены на рис.95-97. На рис.98 в произвольном масштабе одновременно представлены все три характеристики движения. Масштаб можно выбрать таким, что длина вектора будет численно равна амплитуде колебаний. Если же начальное угловое отклонение выбрать численно равным начальной фазе колебаний, то, как легко убедиться, в любой момент времени проекции вектора на оси координат будут изменяться по гармоническому закону, т.е. гармоническое колебание можно представить проекцией вектора, равномерно вращающегося относительно начала координат, на любую из осей. Скорость колеблющегося тела при этом равна
Масштаб можно выбрать таким, что длина вектора будет численно равна амплитуде колебаний. Если же начальное угловое отклонение выбрать численно равным начальной фазе колебаний, то, как легко убедиться, в любой момент времени проекции вектора на оси координат будут изменяться по гармоническому закону, т.е. гармоническое колебание можно представить проекцией вектора, равномерно вращающегося относительно начала координат, на любую из осей. Скорость колеблющегося тела при этом равна  , а ускорение
, а ускорение  . Следовательно, в определённом масштабе для определения скорости и ускорения тела в любой момент времени можно находить проекции векторов, смещённых относительно первого вектора соответственно на
. Следовательно, в определённом масштабе для определения скорости и ускорения тела в любой момент времени можно находить проекции векторов, смещённых относительно первого вектора соответственно на  и
и  , длины которых равны амплитудным значениям скорости и ускорения.
, длины которых равны амплитудным значениям скорости и ускорения.
 В ряде случаев для характеристики колебаний, особенно негармонических, достаточно знать только такую интегральную характеристику, как энергию (или амплитуду), соответствующие заданной частоте. Это имеет место, например, при изучении колебаний систем с несколькими степенями свободы, периодических, но негармонических колебаний, импульсных процессов и т.д.
В ряде случаев для характеристики колебаний, особенно негармонических, достаточно знать только такую интегральную характеристику, как энергию (или амплитуду), соответствующие заданной частоте. Это имеет место, например, при изучении колебаний систем с несколькими степенями свободы, периодических, но негармонических колебаний, импульсных процессов и т.д.


 При гармонических колебаниях закон движения тела можно записать в виде
При гармонических колебаниях закон движения тела можно записать в виде  . Скорость его при этом для произвольного момента времени имеет вид
. Скорость его при этом для произвольного момента времени имеет вид  . Исключая время, получим уравнение фазовой траектории
. Исключая время, получим уравнение фазовой траектории , которая представлена на рис.104.
, которая представлена на рис.104.


