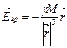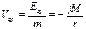Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Продольное сжатие и растяжение. Закон Гука.Содержание книги
Поиск на нашем сайте
При продольном сжатии или растяжении одного упругого образца длинны где Величина С учётом этих обозначений закон Гука для деформации продольного сжатия или растяжения имеет вид: где При изменении продольных размеров одновременно и поперечные. Изменение
Если деформирующая сила изменяется от нуля до
Используя закон Гука, получим: А плотность энергии, соответственно:
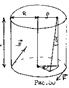
Деформация сдвига. Деформация сдвига возникает при действии на тело касательных усилий (рис. 49). Если к верхней грани образца, имеющего форму параллелепипеда, приложена касательная сила Относительной деформацией называют отношение абсолютной деформации где Поскольку упругие деформации, для которых формулируется закон Гука, имеют место только при маленьких значениях деформации, закон Гука для сдвига принимает вид: Деформация кручения. Деформации кручения возникают при закручивании одного основания образца относительно другого. По закону Гука для этого типа деформации:ы где Величина Одновременно с закручиванием образца происходит сдвиг его слоёв. Угол сдвига Угол сдвига можно получить и из чисто геометрических соображений: Сравнивая (212) и (213), получим Момент распределённых сил, приложенных к нижнему основанию образца, получим, используя (214). Из рис.51 видно, что элементарный момент закручивающих сил, приложенных к элементу основания, равен:
Полный момент: Сравнивая (210) и (216), получаем связь между модулями сдвига и кручения:
Закон всемирного тяготения. Закон всемирного тяготения получен Ньютоном из наблюдений видимого движения планет Солнечной системы, используя законы динамики. В векторной форме закон всемирного тяготения, определяющий силы гравитационного взаимодействия, имеет вид:
где Силовой характер поля источника является сила, действующая на единичную пробную массу, помещённую в данную точку поля. Эта величина называется напряжённостью поля:
Следует отметить, что закон всемирного тяготения справедлив только для точечных взаимодействующих масс. Кроме того, массы тел, фигурирующие в законе всемирного тяготения, имею другой смысл, нежели в законах динамики. Это –“тяготеющие”,”тяжёлые” или ”гравитационные” массы. Потенциальная энергия гравитационного взаимодействия, гравитационный потенциал. Потенциальная энергия взаимодействия численно равна работе сил взаимодействия по перемещению взаимодействующего тела из данного положения в бесконечность:
Энергетической характеристикой поля является гравитационный потенциал, равный потенциальной энергии единичной пробной массы, помещённой в данную точку поля:
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 249; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.19.115 (0.007 с.) |

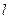 и площади сечения
и площади сечения  удлинение образца
удлинение образца  определяется из опыта выражением:
определяется из опыта выражением: 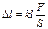
 - коэффициент упругости, определяемый свойствами материала образца.
- коэффициент упругости, определяемый свойствами материала образца.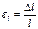 называется относительной деформацией. Величина
называется относительной деформацией. Величина  , обратная коэффициенту упругости, называется модулем упругости Юнга.
, обратная коэффициенту упругости, называется модулем упругости Юнга.

 - называется напряжением (отношение упругих сил в деформированном образце к площади его поперечного сечения).
- называется напряжением (отношение упругих сил в деформированном образце к площади его поперечного сечения). диаметра
диаметра 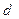 образца (однородного цилиндра) также подчиняется закону Гука:
образца (однородного цилиндра) также подчиняется закону Гука: 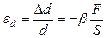 где:
где:  -коэффициент поперечного сжатия при продольном растяжении.
-коэффициент поперечного сжатия при продольном растяжении.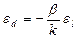 Величина
Величина 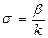 называется коэффициентом Пуассона.
называется коэффициентом Пуассона. 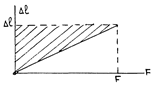
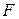 , абсолютная деформация изменяется, соответственно, от нуля до
, абсолютная деформация изменяется, соответственно, от нуля до 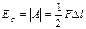
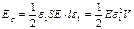

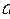 , которое называется абсолютной деформацией при сдвиге.
, которое называется абсолютной деформацией при сдвиге. 
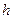 . Для сдвига закон Гука принимает форму:
. Для сдвига закон Гука принимает форму: 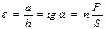
 -коэффициент сдвига, определяемый свойствами материала образца, величина, обратная
-коэффициент сдвига, определяемый свойствами материала образца, величина, обратная 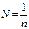
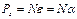

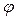 - угол закручивания,
- угол закручивания,  - длинна образца,
- длинна образца,  - момент закручивающих сил,
- момент закручивающих сил,  - коэффициент кручения.
- коэффициент кручения.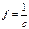 называется модулем кручения т. е.
называется модулем кручения т. е. 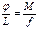
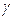 определяется из закона Гука.
определяется из закона Гука. 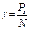
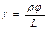
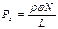

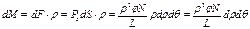
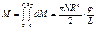
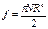
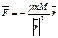
 - величина пробной массы,
- величина пробной массы, 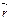 -радиус-вектор точечной пробной массы относительно центра масс источника поля,
-радиус-вектор точечной пробной массы относительно центра масс источника поля,