
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение положения точки в пространстве.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Определение положения точки в пространстве.
Для описания движения точки, т.е. изменения ее положения с течением времени, прежде всего, надо в любой момент времени указать ее местоположение координатным или векторным способом.
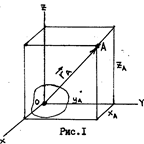
Таким образом, зная координаты точки, можно определить величину (1) радиус-вектора, и его направление в пространстве по так называемым направляющим косинусам (2), (3) и (4). Для определения характеристик движения вводят три вектора: перемещения, скорости и ускорения. ВЕКТОР ПЕРЕМЕЩЕНИЯ.
Для определения перемещения точки в пространстве вводят вектор перемещения.
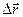 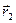  Например, за промежуток времени Dt точка перемещается из положения 1 в положение 2 (рис. 2), определяемые векторным способом указанием радиус-векторов и; вектором перемещения называют вектор, проведенный из начального положения 1 в конечное 2 перемещаемого тела. Из векторного треугольника видно, что вектор перемещения равен приращению радиус-вектора точки. Например, за промежуток времени Dt точка перемещается из положения 1 в положение 2 (рис. 2), определяемые векторным способом указанием радиус-векторов и; вектором перемещения называют вектор, проведенный из начального положения 1 в конечное 2 перемещаемого тела. Из векторного треугольника видно, что вектор перемещения равен приращению радиус-вектора точки.
ВЕКТОР СКОРОСТИ. Вектором скорости называют вектор, определяющий быстроту и направление движения.
Вектором истинной (мгновенной) скорости называют предел, к которому стремится значение вектора средней скорости при бесконечном убывании промежутка времени: Так как при движении тела в общем случае изменяются все три его координаты, часто бывает удобным рассматривать скорость движения точки вдоль отдельных координатных направлений (компоненты или составляющие вектора скорости). Компоненты средней скорости равны:
Компоненты же мгновенной скорости определяются как
ВЕКТОР УСКОРЕНИЯ.
Вектором ускорения называют вектор, определяющий быстроту и направление изменения вектора скорости. Аналогично определениям для вектора скорости вводятся понятия среднего и мгновенного ускорения:
Ускоренное движение Замедленное движение Как видно из рисунков, в обоих случаях вектор dJ направлен в сторону вогнутости траектории. При ускоренном движении он отклоняется в сторону движения, при замедленном - в противоположную
Двигаясь вдоль траектории, за промежуток времени Dt точка проходит путь DS скорость ее изменяется от J до J1, при этом J1 составляет угол Da (альфа) с осью Ot. По определению мгновенного ускорения:

С учетом этих замечаний выражение для нормальной составляющей вектора ускорения принимает вид Для выяснения физического смысла ускорения рассмотрим два частных случая движения. Равномерное криволинейное движение (V=const, k<>0). В этом случае, как видно из (14) и (16),
Неравномерное прямолинейное движение (V<>соnst, K=0). При таком движении Следовательно, касательная составляющая ускорения определяет изменение вектора скорости по величине, а нормальная - по направлению.
Кинематика твердого тела. Для нахождения кинематического закона движения, т.е. r=r(t) или х = х(t), у=y(t), z=z(t) надо найти закон движения каждой точки тела, т.е. решить бесконечно большое число уравнений, что сопряжено с непреодолимыми математическими трудностями. Абсолютно твердое тело – тело у которого расстояние между двумя любыми точками остается постоянно при движении. ЧИСЛО СТЕПЕНЕЙ СВОБОДЫ.
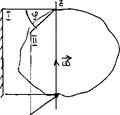
Числом степеней свободы называют число независимых механических координат полностью и однозначно определяющих положение тела в пространстве. Или: число независимых механических движений, которые одновременно может совершать тело. Из таких определений следует, что число степеней свободы для свободной материальной точки равно 3. Для совокупности из n невзаимодействующих между собой точек число степеней свободы равно 3n. Иначе говоря, для точки, движущейся по поверхности, число степеней свободы равно 2. Для точки, движущейся вдоль линии, число степеней свободы равно 1. Рассмотрим теперь систему точек, связанных жесткими связями. Пусть таких точек 2 (рис. 7). Для определения положения одной из точек системы в пространстве нужно указать 3 координаты, т.е. эта часть системы обладает 3-мя степенями свободы. Если эту точку закрепить неподвижно, у системы будет отнято 3 степени свободы. Вторая точка при этом может двигаться только по поверхности сферы, т.е. обладает 2-мя степенями свободы. Следовательно, вся система обладает 5-ю степенями свободы.
Рис. 7 Рис. 8
Аналогично определяется число степеней свободы для системы, состоящей из трех жестко связанных между собой точек (рис. 8). Если одну из точек системы закрепить, у системы отнимается 3 степени свободы При закреплении второй точки дополнительно отнимается еще а степени свободы При этом третья точка сможет двигаться только вдоль линии, т.е. обладает одной степенью свободы. поэтому вся система обладает 6-ю степенями свободы. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТЕЛ.
Вращательным называется такое движение твердого тела, при котором хотя бы две его точки остаются неподвижными в пространстве. Прямая, проходящая через неподвижные точки тела, называются осью вращения. При вращательном движении все точки тела движутся в параллельных плоскостях, описывая концентрические окружности, центры которых лежат на оси вращения. Быстрота вращения определяется угловой скоростью.
Средней угловой скоростью называют величину:
для определения w как вектора необходимо угол поворота (угловое перемещение) также определять как вектор. Вектором углового перемещения называют вектор, направленный вдоль оси вращения в ту сторону, откуда вращение тела видно происходящим против хода часовых стрелок. По такому определению вектор угловой скорости равен: В случае вращения тела, показанном на рис. 10, вектор угловой скорости направлен вверх вдоль оси вращения.
Вектором среднего углового ускорения называют вектор
Легко видеть, что при ускоренном вращении твердого тела вектор углового ускорения направлен вдоль оси вращения в ту же сторону, что и вектор угловой скорости, а при замедленном - вдоль оси вращения противоположно вектору угловой скорости. Сила. Изменение состояния тела происходит в результате взаимодействий, которые приводят к изменению, как внутреннего состояния тел, так и состояния их движения. Количественной мерой взаимодействий, приводящих к изменению состояний тел, является сила. Сила - векторная величина, она характеризуется следующими элементами: величиной, направлением в пространстве и точкой приложения силы. Линия, вдоль которой направлена сила, называется линией действия силы. Совокупность сил, приложенных к телу, называют системой сил. Если под действием системы сил, приложенных к телу, оно может пребывать в состоянии покоя, система называется уравновешенной Сила, равная по величине равнодействующей и противоположно ей направленная, называется уравновешивающей. Силы взаимодействия между телами одной и той же системы называются внутренними. Силы взаимодействия с телами, не входящими в состав данной системы называются внешними. Силы, приложенные в одной точке тела, называются сосредоточенными. Силы, приложенные ко всем точкам поверхности или объема тела, называются распределенными. Основной закон динамики.
Rcosa=h (плечо силы относительно центра окружности). Следовательно, величина mR2 определяет инертные свойства тела при вращательном движении. Эта величина I=mR2 называется моментом инерции тела (точки). С учетом сказанного основной закон динамики для вращательного движения записывают в виде:
Центральными называют силы, линии действия которых проходят в своё время через один и тот же центр. Примером таких сил могут служить силы гравитационного взаимодействия между планетами Солнечной системы.
условия постоянства направления следует, что орбита планеты плоская, т.е. она движется всё время в одной и той же плоскости.
Из рисунка видно, что h*dS равно удвоенной площади, ометаемой радиус-вектором планеты за промежуток времени dt. Обозначив эту площадь dσ, получим:
т.е. площадь, ометаемая радиус-вектором планеты в единицу времени (секториальная скорость) постоянна. Постулаты Эйнштейна. В основе специальной теории относительности, прежде всего, лежит факт постоянства скорости света в различных системах отсчета, что противоречит классическому закону сложения скоростей. Кроме того, нет никаких оснований считать, что механические опьггы позволят отличить одну инициальную систему отсчета от другой. Это позволило Эйнштейну сформулировать исходные постулаты специальной теории относительности. Постулат о постоянстве скорости света: скорость света в вакууме одинакова во всех инерциальных системах отсчета и не зависит от движения источника и приемника света. Постулат относительности (общефизический принцип относительности): Никакими физическими опытами нельзя отличить одну инерциальную систему отсчета от другой. Наряду с этими постулатами Эйнштейн ввел принцип синхронизации часов, имеющий такое же значение в теории относительности, как и сформулированные выше постулаты. Для того, чтобы одинаковые по устройству часы А и В (рис.31)
"Радиолокационный" метод (метод коэффициента "k "). Движение тел можно графически представлять диаграммами x=x(t). В случае скоростей, сравнимых со скоростью света, масштаб х и t выбирается таким, что траектория светового сигнала ("световая линия") делит координатный угол пополам. Если же тело движется со скоростью, меньшей скорости света, угол наклона его траектории к оси t меньше 45°. Предположим, что две инерциальные системы отсчета А и В находятся в относительном движении. Систему А условно считаем неподвижной. В исходный момент времени системы полностью совпадали. В этот момент осуществляется синхронизация подвижных и неподвижных часов и на них устанавливаются нулевые показания. Далее система В удаляется от А со скоростью v<c (рис.32).
= kt
С момента синхронизации до отражения сигнала система В и световой сигнал, посланный в момент времени t (по часам А), проходят одинаковый путь:
откуда получаем значение коэффициента k:
18. "Замедление" хода времени.
Следовательно, промежуток времени между двумя событиями, измеренный подвижными часами, меньше результата того же измерения по неподвижным часам. Относительная скорость. Предположим, что системы А, В и D находятся в относительном движении. В исходный момент все три системы совпадали. В этот момент производим синхронизацию всех часов и устанавливаем на них нулевые показания. Далее система В удаляется от А со скоростью v1, а система D - со скоростью v2 >v1. В момент времени t (пo часам А) в системе А производится световая вспышка, сигнал от которой достигает
системы В в момент tB =k1t (по часам В) и системы D в момент tD = k2t (по часам D ). При этом: Теперь будем считать систему В неподвижной, а систему D - удаляющейся от B с относительной скоростью и. Тогда:
откуда: Это и есть выражение для относительной скорости.
19. Сравнение поперечных размеров тел.
Пусть две системы OXYZ и O'X'Y'Z' находятся в относительном движении. Одну из них, OXYZ, считаем неподвижной, другая же движется со скоростью v относительно первой так, что оси ОХ, 0'Х' и 0Z, О’Z' остаются параллельными, а ось О’Y' скользит вдоль оси OY. В подвижной системе вдоль оси O'Z' расположены "световые часы" (жесткий стержень с двумя зеркалами на концах, отражающими поверхностями друг к другу) так, что нижнее зеркало совпадает с началом системы отсчета (рис.34). В исходный момент, когда системы полностью совпадали, у нижнего зеркала произошла световая вспышка. Сигнал от нее достигает верхнего зеркала, отражается, приходит опять к нижнему зеркалу, и далее процесс повторяется периодически. Пусть по неподвижным часам промежуток
времени между вспышкой и приходом сигнала равен t. За это время в неподвижной системе световой сигнал проходит путь сt, а подвижная система - vt. Из рисунка видно, что длина световых часов, численно равная координате z верхнего зеркала, в неподвижной системе равна:
В подвижной системе, связанной с подвижными часами, длина их равна: z'=ct'
т.е. поперечные размеры (по отношению к направлению движения) тел одинаковы в обеих системах отсчета: z'=z Эффект "сокращения" длин.
времени t1 по неподвижным часам (рис.35). Тогда: где: l - длина световых часов, измеренная в неподвижной системе.
Период световых часов, измеренный в неподвижной системе, равен:
где l' - длина часов, измеренная в подвижной системе.
Следовательно, продольные размеры тел в любой системе меньше собственных:
20. Преобразования Лоренца.
Учитывая, что поперечные размеры тел одинаковы, получаем: z'=z
Для сравнения координат у обратимся к предыдущему примеру:
Интервал. Инвариантность интервала.
где xi,yi,zi,ti - пространственные и временные координаты событий.
Таким образом, интервал является инвариантом S /2=S 2
1.Времениподобные интервалы (cΔt > Δl). 2.Пространственноподобные интервалы (cΔt <s Δl). 3. Светоподобные интервалы (сΔt = Δl). 21. Релятивистская масса, релятивистский импульс.
Масса тела, движущегося со скоростью n, равна:
Соответственно, импульс тела определяется выражением: Силы инерции. Как уже отмечалось, существуют такие системы отсчета, в которых ускорение тел вызывается не только действием сил, но и самим движением системы отсчета. Рассмотрим поведение свободного тела, находящегося в покое относительно неподвижной системы. В этой системе выполняются законы Ньютона: равнодействующая приложенных к телу сил равна нулю и тело, как следствие, находится в покое. Если же другая система отсчета движется относительно первой с ускорением a, то в подвижной системе тело получает ускорение - а, равное по величине ускорению системы и противоположно ему направленное. Следовательно, в подвижной системе законы Ньютона не выполняются: равнодействующая приложенных сил равна нулю, а тело приобретает ускорение.
объясняющая появление ускорения тепа в подвижной системе отсчета. Т.е. сила инерции равна произведению массы тела на ускорение системы и противоположно ему направлена. Если связать систему отсчета с ускоренно движущимся телом, то геометрическая сумма всех сил, приложенных к телу, включая силу инерции, равна нулю (принцип Даламбера) Силы инерции Кориолиса.
Абсолютный импульс тела определяется относительным и переносным движением
Со временем будут изменяться обе составляющие абсолютного импульса. Рассмотрим сначала изменение относительного импульса. Поскольку тело движется равномерно относительно подвижной системы, будет изменяться только направление импульса. За промежуток времени система (и ее радиус) поворачивается на угол Dj = wDt (рис. 37).
 При малых углах поворота вращение относительного импульса равно: При малых углах поворота вращение относительного импульса равно:
Изменение величины переносного импульса за время dt равно
С другой стороны, из основного закона динамики следует: где F - равнодействующая приложенных к телу сил.

Учитывая направления (рис. 39) векторов в векторном виде можно записать
В системе, связанной с вращающимся стержнем, тело движется равномерно и прямолинейно, т.е. сумма приложенных к нему сил должна быть равной нулю. Как видно из рисунка, в горизонтальной плоскости силы не уравновешены, поэтому необходимо для выполнения законов динамики ввести силы инерции (на рисунке показаны пунктиром). Вдоль стержня действует центробежная сила инерции, уравновешивающая центростремительную силу.
Как видно из, сила Кориолиса возникает во вращающейся системе отсчета при относительном движении тел. Силы трения. Сухое трение.
Сухим (внешним) трением называют силы сопротивления движению, возникающие при относительном движении одного твердого тела по поверхности другого. Силы сопротивления движению определяются наличием микро- и макронеровностей поверхностей трущихся тел и взаимодействием между ними. При скольжении одной твердой поверхности по другой в плоскости соприкосновения тел возникают силы, направленные противоположно относительной скорости. Эти силы и называют силами трения скольжения. Коэффициент трения скольжения k является безразмерной величиной и определяется природой и состоянием поверхностей трущихся тел. Кроме закона Кулона опытным путем установлен ряд закономерностей для трения скольжения среди которых наиболее часто употребляются следующие: 1. При попытке сдвинуть одно тело по поверхности другого в плоскости контакта возникают силы, сопротивления, изменяющиеся от нуля до предельного значения, называемого силой трения покоя. 2. С увеличением относительной скорости трущихся тел силы - трения сначала убывает, а затем начинают возрастать. 3. Силы трения тем меньше, чем тверже трущиеся поверхности. Силы трения качения.
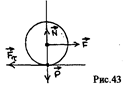
Сопротивление качению может возникать в том случае, если нормальная реакция смещается относительно вертикального диаметра катка в сторону движения. Это происходит в том случае, если давление катка на поверхность будет не в точке, а по участку поверхности, а интенсивность давления будет больше впереди вертикального диаметра катка, как показано на рис. 44.
Следовательно, поверхность должна деформироваться, причем деформации будут несимметричными относительно вертикального диаметра. Положим, что сила Здесь Вязкое трение Вязкое трение возникает при относительном движении слоёв жидкости или газа. Основные законы вязкого трения получены опытным путём. Ньютон установил, что если под действием силы площадка На подвижную площадку действуют силы сопротивления движению (силы вязкого трения): где При движении тел в вязкой среде на них действуют силы сопротивления движению. Стокс получил выражение для этих сил. При малых скоростях.
где:
Движение тел в сопротивляющейся среде. При достаточно больших скоростях тел (или если форма тела является плохо обтекаемой) силы Стокса становятся пропорциональны квадрату скорсти: Положим, что тело начинает падать под действием силы тяжести в сопротивляющейся среде. Пренебрегая силой Архимеда, запишем: С течением времени скорость тела возрастает, возрастает и сила Стокса. Наконец, силы тяжести и Стокса уравновешиваются, после чего начинается равномерное движение тела с установившейся скоростью
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 868; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.86.104 (0.012 с.) |



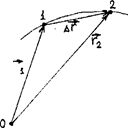
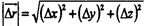

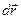


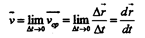
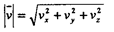





 Поэтому вектор ускорения лежит в плоскости, содержащей касательную к траектории в данной точке и прямую, параллельную касательной в соседней точке траектории.
Поэтому вектор ускорения лежит в плоскости, содержащей касательную к траектории в данной точке и прямую, параллельную касательной в соседней точке траектории.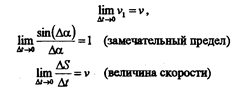


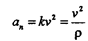 :
:



 а мгновенной:
а мгновенной:

 а мгновенного
а мгновенного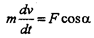 Пусть точка движется по окружности радиуса с центром в т. О под действием силы F, составляющей угол a с касательной а окружности (рис. 26).
Пусть точка движется по окружности радиуса с центром в т. О под действием силы F, составляющей угол a с касательной а окружности (рис. 26).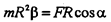
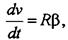
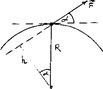
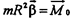
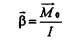
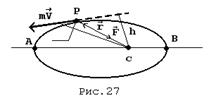
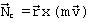
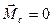
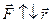
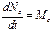
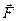
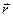 Основные особенности движения тел в поле центральных сил рассмотрим на примере движения планеты вокруг Солнца. Планета Р (рис.27) движется вокруг Солнца, центр масс которого находится в точке с. Радиус-вектор планеты, а сила, действующая на неё со стороны Солнца -. Движение планеты вокруг Солнца описывается уравнением моментов:
Основные особенности движения тел в поле центральных сил рассмотрим на примере движения планеты вокруг Солнца. Планета Р (рис.27) движется вокруг Солнца, центр масс которого находится в точке с. Радиус-вектор планеты, а сила, действующая на неё со стороны Солнца -. Движение планеты вокруг Солнца описывается уравнением моментов: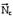 Т.к.., следовательно:
Т.к.., следовательно: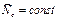 Постоянство вектора означает постоянство как его модуля, так и направления в пространстве. Из
Постоянство вектора означает постоянство как его модуля, так и направления в пространстве. Из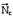
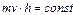
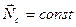 Из условия постоянства модуля вектора следует, что:
Из условия постоянства модуля вектора следует, что: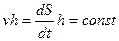
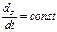
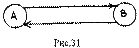
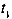
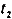 шли одинаково, необходимо их синхронизировать. Пусть в момент времени, отсчитанный по часам А, в том месте, где они находятся, осуществляется световая вспышка. Сигнал от нее достигает часов В, мгновенно отражается и поступает к часам А в момент времени, отсчитанный по ним. Часы А и В считаются синхронизированными, если в момент отражения сигнала в т. В показания часов равны:
шли одинаково, необходимо их синхронизировать. Пусть в момент времени, отсчитанный по часам А, в том месте, где они находятся, осуществляется световая вспышка. Сигнал от нее достигает часов В, мгновенно отражается и поступает к часам А в момент времени, отсчитанный по ним. Часы А и В считаются синхронизированными, если в момент отражения сигнала в т. В показания часов равны: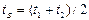

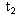
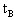
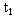
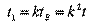 Системы равноправны, поэтому с момента отражения неподвижной можно считать систему В, а систему А - подвижной. Тогда показания часов А в момент приема сигнала равны:
Системы равноправны, поэтому с момента отражения неподвижной можно считать систему В, а систему А - подвижной. Тогда показания часов А в момент приема сигнала равны: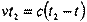 т.е
т.е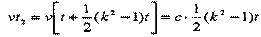
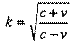
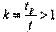 Следовательно, показания подвижных часов в момент приема сигнала всегда больше показаний неподвижных часов в момент посылки сигнала:
Следовательно, показания подвижных часов в момент приема сигнала всегда больше показаний неподвижных часов в момент посылки сигнала: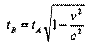
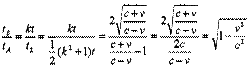
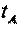
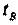 Рассмотрим промежуток времени между двумя событиями (синхронизация часов и отражение сигнала), измеренный по часам А и В. Поскольку в момент синхронизации показания обоих часов нулевые, то промежуток времени численно равен показаниям часов в момент отражения сигнала. Обозначив промежуток времени, измеренный по часам А и В, соответственно и, отношение этих показаний запишем в виде:
Рассмотрим промежуток времени между двумя событиями (синхронизация часов и отражение сигнала), измеренный по часам А и В. Поскольку в момент синхронизации показания обоих часов нулевые, то промежуток времени численно равен показаниям часов в момент отражения сигнала. Обозначив промежуток времени, измеренный по часам А и В, соответственно и, отношение этих показаний запишем в виде: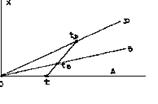
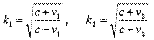
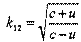
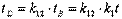
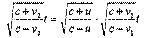
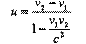 Следовательно:
Следовательно: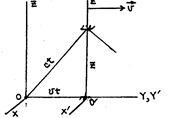
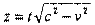
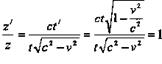 где: t ' - полупериод часов, т.е. промежуток времени между вспышкой и приходом сигнала к верхнему зеркалу.Учитывая эффект "замедления" хода времени, получаем:
где: t ' - полупериод часов, т.е. промежуток времени между вспышкой и приходом сигнала к верхнему зеркалу.Учитывая эффект "замедления" хода времени, получаем:
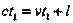 Пусть теперь световые часы ориентированы вдоль оси подвижной системы так, что левое зеркало совпадает с ее началом. В исходный момент системы совпадали, и в этот момент у левого зеркала произошла вспышка. Сигнал от нее достигает правого зеркала через промежуток
Пусть теперь световые часы ориентированы вдоль оси подвижной системы так, что левое зеркало совпадает с ее началом. В исходный момент системы совпадали, и в этот момент у левого зеркала произошла вспышка. Сигнал от нее достигает правого зеркала через промежуток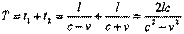
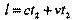 После отражения сигнал и левое зеркало движутся навстречу друг другу и встречаются в момент времени t2 по неподвижным часам. Очевидно, что:
После отражения сигнал и левое зеркало движутся навстречу друг другу и встречаются в момент времени t2 по неподвижным часам. Очевидно, что: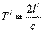 В подвижной системе период часов определяется соотношением:
В подвижной системе период часов определяется соотношением: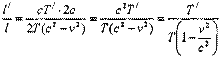
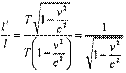
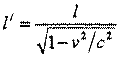
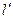
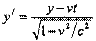 Преобразования Лоренца дают связь между пространственными и временными координатами событий в двух инициальных системах отсчета, находящихся в относительном движении.
Преобразования Лоренца дают связь между пространственными и временными координатами событий в двух инициальных системах отсчета, находящихся в относительном движении.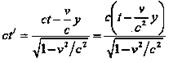 х'=x
х'=x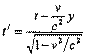
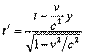 С другой стороны, это соотношение можно представить в виде:
С другой стороны, это соотношение можно представить в виде: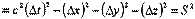 Интервалом S между двумя событиями называют величину, квадрат которой равен:
Интервалом S между двумя событиями называют величину, квадрат которой равен: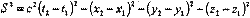
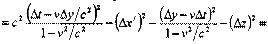
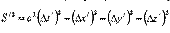 Используя преобразования Лоренца, запишем интервал в подвижной системе отсчета:
Используя преобразования Лоренца, запишем интервал в подвижной системе отсчета: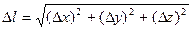 В зависимости от соотношения между временной cΔt и пространственной частями интервала различают:
В зависимости от соотношения между временной cΔt и пространственной частями интервала различают: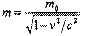 Из факта предельности скорости света следует, что тела могут двигаться только со скоростями, меньшими скорости света. Если на тело действует постоянная сила, то его ускорение пропорционально силе лишь при малых скоростях. С ростом скорости при неизменной силе ускорение начинает уменьшаться, что можно объяснить только возрастанием массы тела с ростом скорости.
Из факта предельности скорости света следует, что тела могут двигаться только со скоростями, меньшими скорости света. Если на тело действует постоянная сила, то его ускорение пропорционально силе лишь при малых скоростях. С ростом скорости при неизменной силе ускорение начинает уменьшаться, что можно объяснить только возрастанием массы тела с ростом скорости.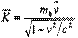
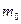 Где, - масса тела в системе, связанной с ним, так называемая "масса покоя".
Где, - масса тела в системе, связанной с ним, так называемая "масса покоя". Чтобы и в таких системах выполнялись законы Ньютона, приходится вводить дополнительные фиктивные силы, называемые силами инерции. В рассмотренном примере в подвижной системе вводится сила инерции:
Чтобы и в таких системах выполнялись законы Ньютона, приходится вводить дополнительные фиктивные силы, называемые силами инерции. В рассмотренном примере в подвижной системе вводится сила инерции: Пусть система вращается равномерно с угловой скоростью ω. Вдоль радиуса системы равномерно со скоростью v движется тело (рис. 36).
Пусть система вращается равномерно с угловой скоростью ω. Вдоль радиуса системы равномерно со скоростью v движется тело (рис. 36).

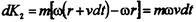
 полное изменение импульса тела равно
полное изменение импульса тела равно
 Таким образом, наблюдаемые изменения импульса вызываются внешними силами, равными по величине: F=2mnw
Таким образом, наблюдаемые изменения импульса вызываются внешними силами, равными по величине: F=2mnw






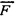
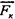 Силу уравновешивает сила инерции Кориолиса:
Силу уравновешивает сила инерции Кориолиса:
 Трение качения возникает при качении одного твердого тела по поверхности другого. При попытке сдвинуть тело по поверхности другого в плоскости соприкосновения возникает
Трение качения возникает при качении одного твердого тела по поверхности другого. При попытке сдвинуть тело по поверхности другого в плоскости соприкосновения возникает сила препятствующая этому.
сила препятствующая этому.
 вызывает равномерное качение катка, т.е.
вызывает равномерное качение катка, т.е. 

 (коэффициент трения качения) является размерной величиной. Смысл его- ''плечо'' нормальной составляющей реакции поверхности.
(коэффициент трения качения) является размерной величиной. Смысл его- ''плечо'' нормальной составляющей реакции поверхности. площади
площади 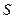 движется равномерно со скоростью
движется равномерно со скоростью  относительно площадки
относительно площадки  ,
, 

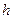 - расстояние между площадками (слоями),
- расстояние между площадками (слоями),  - коэффициент вязкого трения определяемая свойствами вязкой среды, заполняющей промежуток между площадками.
- коэффициент вязкого трения определяемая свойствами вязкой среды, заполняющей промежуток между площадками.
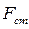 - стоксова сила сопративления,
- стоксова сила сопративления,  - плотность среды,
- плотность среды,  -коэффициент, определяемый геометрией тела,
-коэффициент, определяемый геометрией тела, 


 . Определим зависимость скорост
. Определим зависимость скорост 


