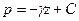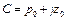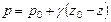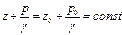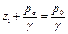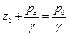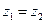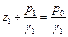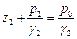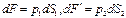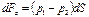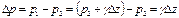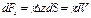Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Давление покоящейся жидкости.Содержание книги
Поиск на нашем сайте
Выделим в объеме покоящейся жидкости небольшой объем (рис. 68), пусть на грань этого объема действует со стороны окружающих слоев сила давления F. Из опыта известно, что трение покоя в жидкостях отсутствует, т.е. должны отсутствовать касательные усилия к выделенной грани. Средним давлением называют величину: где dF сила давления, действующая на площадку площади dS. Истинным давлением или давлением в точке называют величину: В покоящейся жидкости давление в точке не зависит от ориентировки площадки, на которую оно действует, действительно, в покоящейся: жидкости выделим небольшой объем, форма которого показана на рис. 69. На каждую грань объема действует силы давления, поскольку объем покоится, в каждом из координатных направлений сумма сил равна нулю:
УРАВНЕНИЕ ГИДРОСТАТИКИ ЭЙЛЕРА В покоящейся жидкости выделим малый ее объем dV=dxdydz в форме прямоугольного параллелепипеда (рис. 70). Известно давление в центре объема p и изменение давления на единицу длины в каждом из координатных направлений:
На каждую грань объема действуют силы давления, а на весь объем - объемные (массовые) силы, например, сила тяжести. Поскольку объем покоится, сумма проекции всех сил по каждому из координатных направлений равна нулю. На заднюю грань действует сила давления:
Кроме того, в этом направлении действует составляющая массовой силы dq, которую можно определить по второму закону Ньютона:
где: r - плотность среды, ax- ускорение, которое способна сообщить массовая сила. Т. к. объем покоится,
Поскольку
Аналогично для других координатных направлений:
УРАВНЕНИЕ ПОВЕРХНОСТИ УРОВНЯ Поверхностью уровня называют такую поверхность, во всех точках которой давление одинаково (dP=0)
то, с учетом уравнение Эйлера:
для поверхности уровня:
В случае идеальной жидкости:
Пример, Пусть жидкость покоится в поле тяготения 3емли. Плоскость 0XY горизонтальна, а ось z направлена вертикально вверх. В этом случае:
Тогда:
т.е. z=const, т.о. поверхности уровня (в частности, свободная поверхность) горизонтальны.
ЗАКОН ПАСКАЛЯ Жидкость покоится в поле тяготения Земли. В этом случае уравнения Эйлера имеют вид:
С учетом и последнее уравнение принимает вид: откуда: где Постоянная интегрирования будет определена, если в точке с координатой z0 известно давление p0. Тогда
Последнее выражение обычно записывают в виде: т.е. для жидкости, покоящейся в поле тяготения Земли, сумма геометрической (Z) и пьезометрической (p/g)) высот для всех точек объема жидкости одинакова. Это и есть закон Паскаля.
СООБЩАЮЩИЕСЯ СОСУДЫ ЗАПОЛНЕНЫ ОДНОРОДНОЙ ЖИДКОСТЬЮ Свободные поверхности в левом и правом коленах находятся на уровнях Z1 и Z2, а давление на этих поверхностях равно атмосферному Рa. Сравним свободные поверхности с общей для обоих сосудов частью, уровнем Z0, на котором давление равно P0, как показано на рис. 71.
Откуда:
Следовательно, свободные поверхности устанавливаются на одном уровне. СООБЩАЮЩИЕСЯ СОСУДЫ ЗАПОЛНЕННЫЕ НЕОДНОРОДНОЙ ЖИДКОСТЬЮ
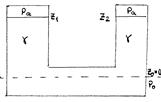
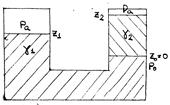
Положим, что сосуды заполнены неоднородной жидкостью (несмешивающимися жидкостями с удельными весами g1 и g2. Через границу раздела жидкостей проводим уровень Z0 =0, на котором давление равно Р0 (рис. 72). Сравним свободную поверхность в левом сосуде с границей раздела со стороны жидкости с удельным весом g1: для правого сосуда аналогично: Сравнивая записанные выражения, получим, что свободные поверхности в сосудах устанавливаются на уровнях, обратно пропорциональных удельным весам жидкостей:
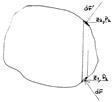
ЗАКОН АРХИМЕДА Тело погружено в жидкость (рис. 73).
На его поверхность со стороны жидкости действуют силы давления, выделим в теле объем малого сечения, ось которого вертикальна. На верхнюю и нижнюю грани этого объема действуют силы давления: Равнодействующая сил давления в проекции на вертикальную ось равна: где: dS - проекция dS1 (или dS2) на горизонтальную плоскость. Разность давлений по закону Паскаля равна где: dZ - разность уровней центров граней выделенного объема. Тогда равнодействующая сил давления равна где dV - величина выделенного объема. Вертикальная проекция сил давления, действующих на всю смоченную поверхность тела, может быть получена путем интегрирования предыдущего выражения: т.е. сила, действующая со стороны жидкости на погруженное в нее тело по величине равна весу жидкости, вытесненной телом. Формулировка закона: на тело, погруженное в жидкость действует выталкивающая сила, равная весу жидкости в объеме, вытесненном телом, и приложенная в той точке смоченной поверхности тела, в которой вертикаль, проведенная через центр масс вытесненной жидкости, пересекает эту поверхность. Существенным в формулировке закона Архимеда является правильное указание точки приложения выталкивающей силы
|
||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 732; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |


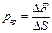

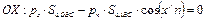
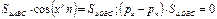

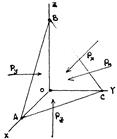 Аналогично можно показать, что:
Аналогично можно показать, что: 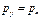
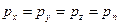

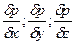
 а на переднюю:
а на переднюю: 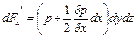
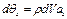
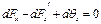
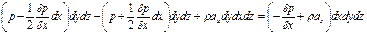
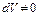 :
: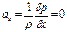
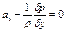
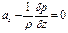 и представляют собой систему уравнений гидростатики Эйлера.
и представляют собой систему уравнений гидростатики Эйлера.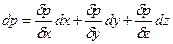
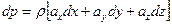
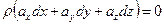
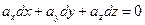
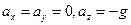
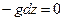
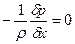
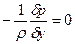
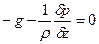
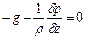
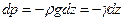
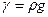 удельный вес жидкости. Интегрируя, получаем
удельный вес жидкости. Интегрируя, получаем