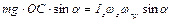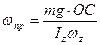Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нормировка потенциальной энергии, закон сохранения энергии.Содержание книги
Поиск на нашем сайте
Положим, что в замкнутой консервативной системе выделены состояния 1, 2 и 3, условно принятое за исходное, При переходе из состояний 1, 2 в исходное (рис. 57) работа консервативных сил равна:
Т.е. для любых состояний системы кинетическая энергия в этом состоянии и работа внутренних сил по переходу из выбранного состояния в исходное - величина постоянная для всех состояний системы. Для расчетов важно, чтобы работа сил на любом переходе имела одинаковый знак, поэтому в выражении к значению работы надо добавить такую положительную величину
Сама проделанная операция выбора Момент инерции твёрдого тела. Момент инерции твердого тела равен сумме моментов инерции отдельных его частиц: где Предположим, что масса выделенной частицы тела Момент инерции относительно т. О по определению равен
а относительно координатных осей:
Если одним из размеров тела можно пренебречь по сравнению с двумя другими (плоское тело), эта связь запишется в виде
Если стержень имеет массу
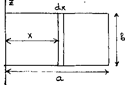
Момент инерции тонкой пластины прямоугольной формы относительно одной из её сторон.
Размеры тонкой пластины массы
Момент инерции однородного шара относительно его центра. Пусть масса шара равна
Теорема Штейнера. Расчет моментов инерции тела даже правильной формы, если ось не проходит через центр масс тела, затруднен. В этом случае удобно пользоваться теоремой Штейнера: Момент инерции тела относительно произвольной оси
Момент инерции тела относительно Из геометрических соображений: Первое слагаемое в правой части дает момент инерции тела относительно Поскольку a=const, второе слагаемое принимает вид (Ma2), где М - масса тела. В последнем слагаемом: следовательно, по определению центра масс: последнее слагаемое обращается в нуль, поэтому: Кинетическая энергия твёрдого тела для различных типов движения. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ
ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ
ПЛОСКОЕ ДВИЖЕНИЕ ТЕЛА
где: 2. Вращательное движение СВОБОДНЫЕ ОСИ ВРАЩЕНИЯ Момент импульса тела в произвольном случае его вращения не совпадает по направлению с вектором угловой скорости вращения. Такие оси называются главными осями инерции (свободными осями вращения). Таких осей в каждом теле три, все они взаимноперпендикулярны и проходят через центр масс тела, поэтому их удобно принимать в качестве системы отсчета для каждой из этих осей
В случае произвольного по форме тела легко показать, что Кинетическая энергия тела при таком вращении может быть представлена суммой энергий вращения вокруг трех главных осей: Направление векторов
очевидно, что направления Твердое тело, отвечающее условию, называется шаровым волчком. Твердое тело, у которого Твердое тело, у которого все три главных момента инерции различны, называет несимметричным волчком СВОБОДНОЕ ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА Свободным называют такое вращение тела, при котором сумма моментов внешних сил, приложенных к телу, равна нулю:
Отсюда следует, что при свободном вращении:
Рассмотрим свободное вращение симметричного волчка с осью симметрии
В этом выражении первое слагаемое постоянно, следовательно, постоянно и второе, т.е.: Учитывая, что Написав выражение для кинетической энергии в виде: вывод: наконец, кинетическую энергию представим в виде: где a - угол между векторами
Учитывая свободное вращение тела можем представить как вращение оси симметрии тела вокруг неподвижного направления
Т. o. для вращающегося тела можно выделить три оси - момента импульса., угловой скорости и оси симметрии. Существенно, что относительное расположение этих осей зависит от величины угловой скорости вращения тела вокруг оси симметрии Гироскопы. Рассмотрим быстро вращающийся относительно оси симметрии массивный диск. При очень быстром вращении диска, как было сказано выше, векторы момента импульса и угловой скорости направлены вдоль оси симметрии. Если к концам оси вращения приложить пару сил, ее момент будет изменять момент импульса в соответствии с уравнением моментов:
Через промежуток времени Уравнение моментов в скалярном виде в этом случае представляют следующим образом: С учетом направлений векторов уравнение моментов для быстро вращающегося тела записывает в векторной форме так:
Гироскопом называют массивное тело, очень быстро вращающееся вокруг оси симметрии. Наиболее часто применяются гироскопы в кардановых подвесах. В таких подвесах при любом повороте оси вращения центр масс гироскопа остается неподвижным (рис.65) Нa рисунке представлен карданов подвес для гироскопа с двумя степенями свободы.
Для определения угловой скорости прецессии удобно пользоваться следующими соображениями. Масштаб измерения При действии на конец оси (в т. А) силы Но Прецессия волчка. Быстро вращающийся симметричный волчок установлен на горизонтальную поверхность (рис. 67). Точка касания при указанном направлении вращения момент силы тяжести вызывает прецессию в направлении, указанном на рисунке. Угловую скорость прецессии
(рис. 67) можно определить, пользуясь (274):
Следовательно, угловая скорость прецессии тем меньше, чем больше угловая скорость собственного вращения.
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 390; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.133.214 (0.007 с.) |


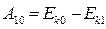

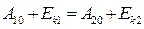
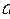 , чтобы:
, чтобы:

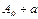 - потенциальной энергией системы в данном состоянии. С учетом сказанного:
- потенциальной энергией системы в данном состоянии. С учетом сказанного:  для всех состояний системы. Это и есть закон сохранения механической энергии.
для всех состояний системы. Это и есть закон сохранения механической энергии.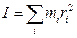
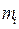 - масса
- масса  -й частицы тела,
-й частицы тела,  - ее расстояние от заданного центра или оси.
- ее расстояние от заданного центра или оси.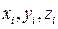 .
.
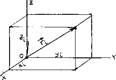



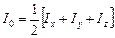
 Момент инерции тонкого стержня относительно оси, перпендикулярной стержню и проходящий через его центр масс.
Момент инерции тонкого стержня относительно оси, перпендикулярной стержню и проходящий через его центр масс.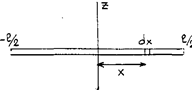
 и длину
и длину 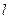 , а ось
, а ось  проходит через центр масс стержня, то координаты левого и правого концов стержня равны -
проходит через центр масс стержня, то координаты левого и правого концов стержня равны -  и
и 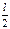 . Выделим в стержне на расстоянии
. Выделим в стержне на расстоянии 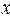 от оси малый его участок длины
от оси малый его участок длины 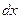 . Его момент инерции относительно
. Его момент инерции относительно 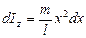
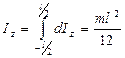
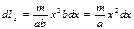
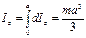
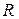 . Выделим в шаре тонкий сферический слой радиуса
. Выделим в шаре тонкий сферический слой радиуса 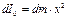
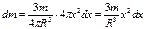
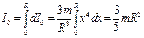
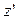 равен сумме момента инерции относительно оси
равен сумме момента инерции относительно оси 
 Для доказательства через центр масс тела (т. С) проведем ось
Для доказательства через центр масс тела (т. С) проведем ось 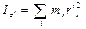


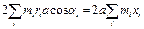


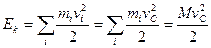


 и
и  - моменты инерции тела относительно осей, проходящих через центр масс и мгновенный центр вращения,
- моменты инерции тела относительно осей, проходящих через центр масс и мгновенный центр вращения, 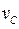 . - скорость центра масс поступательной части движения),
. - скорость центра масс поступательной части движения),  (омега) - угловая скорость вращения вокруг оси, проходящей через центр масс.
(омега) - угловая скорость вращения вокруг оси, проходящей через центр масс. ,
,  ,
,  .
. и
и  или:
или: 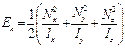 или:
или:  или:
или: 
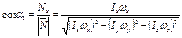
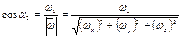
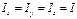
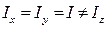 , называется симметричным волчком с осью симметрии
, называется симметричным волчком с осью симметрии 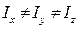 .
.




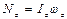 получаем:
получаем: 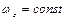
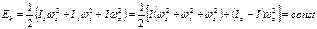
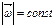

 и
и  .Из следует, что,
.Из следует, что, 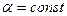
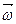 ,
, 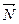 и
и 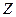 со временем сохраняется (рис.53). Такое вращение при отсутствии моментов внешних сил называется регулярной прецессией. Тело вращается вокруг оси симметрии со скоростью
со временем сохраняется (рис.53). Такое вращение при отсутствии моментов внешних сил называется регулярной прецессией. Тело вращается вокруг оси симметрии со скоростью 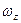 , a сама ось описывает коническую поверхность, вращаясь вокруг неподвижного направления
, a сама ось описывает коническую поверхность, вращаясь вокруг неподвижного направления  .
.
 . Несложно доказать, что при очень быстром вращении тела
. Несложно доказать, что при очень быстром вращении тела  все три направления практически сливаются в одно. Эта особенность быстро вращающихся тел лежит в основе элементарной теории гироскопов.
все три направления практически сливаются в одно. Эта особенность быстро вращающихся тел лежит в основе элементарной теории гироскопов.
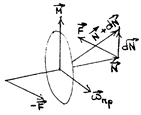
 момент импульса изменит свое направление и станет равным
момент импульса изменит свое направление и станет равным 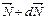 Соответственно изменится и положение оси симметрии. Как видно, силы пары приложены в горизонтальной плоскости, а ось вращается под действием момента - в вертикальной.
Соответственно изменится и положение оси симметрии. Как видно, силы пары приложены в горизонтальной плоскости, а ось вращается под действием момента - в вертикальной.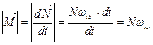


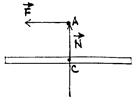
 ее момент вызовет прецессионное вращение. По уравнению моментов
ее момент вызовет прецессионное вращение. По уравнению моментов 
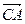 можно рассматривать как радиус-вектор т. A относительно центра масс. Тогда, по определению:
можно рассматривать как радиус-вектор т. A относительно центра масс. Тогда, по определению: 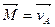
 неподвижна. Прецессия волчка вызывается моментом силы тяжести так как линия действия реакции проходит через неподвижный центр
неподвижна. Прецессия волчка вызывается моментом силы тяжести так как линия действия реакции проходит через неподвижный центр