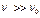Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Механика движущихся жидкостей.Содержание книги
Поиск на нашем сайте
При изучении движения жидкостей и газов применяются различные способы описания движения. Наиболее часто используется метод, предложенный Эйлером. Но Эйлеру в области пространства, занятой движущейся жидкостью, выделяется точка, в которой определяются параметры движения различных жидких частиц, проходящих через эту точку в различные моменты времени. Основной задачей механики движущейся жидкости является нахождение распределений скорости, плотности и давления по потоку жидкости:
1.Линией тока называют кривую, в каждой точке которой касательные к ней совпадают по направлению с вектором скорости в данный момент времени. 2.Поверхностью тока называют поверхность, образованную линиями в тока. 3.Поверхность тока, проходящую через замкнутый контур, называют трубкой тока. 4.Часть потока жидкости, ограниченную трубкой тока, называют струёй жидкости. Пpи установившемся потоке жидкость внутри трубки тока а движется как в трубке с твердыми стенками. РАСХОД ЖИДКОСТИ Различают объемный, массовый и весовой расходы жидкости. Объемным расходом называют объем жидкости, протекающий в единицу времени через заданную площадку. Для площадки элементарно малой площади dS объемный расход равен:
Аналогично массовый расход определяется величиной протекающей через площадку массы жидкости в единицу времени:
Вес жидкости, протекающей через площадку в единицу времени, называют весовым расходов: В этих выражениях: УРАВНЕНИЕ НЕРАЗРЫВНОСТИ СТРУИ ЖИДКОСТИ Оделим участок струи жидкости (рис.74). Через левое сечение площади S1 в участок трубки тока в единицу времени втекает жидкость со скоростью v1, принимаемой одинаковой по сечению. Массовый расход жидкости в этом сечении равен: Аналогично массовый расход для правого сечения равен:
ЯЧ Для того, чтобы в выделенном участке трубки тока не происходило накопление жидкости или, наоборот, уменьшение массы, массовые расходы в левом и правом сечениях должны быть равны. Такой вывод можно сделать для любого другого сечения, т.е.: Это и есть уравнение неразрывности струн жидкости. В случае несжимаемой жидкости: УРАВНЕНИЕ БЕРНУЛЛИ Как и для твёрдых тел, для жидкости полная механическая энергия состоит из потенциальной и кинетической энергии, кинетическая энергия движущейся массы жидкости равна: Что касается потенциальной энергии, то она будет определяться не только положением жидкости в поле тяготения Земли, но и внутренним состоянием ее. Соответственно, различают потенциальную энергию положения: И потенциальную энергию состояния жидкости: Полная энергия движущейся жидкости равна: Удельной энергией называют полную энергию, приходящуюся на единицу веса жидкости: В такой записи все члены удельной энергии имеют размерность длины и называются соответственно: геометрической, пьезометрической высотой и высотой скоростного напора.
В установившемся потоке невязкой жидкости выделим участок трубки тока (рис.75). Высоты центров сечений, давление, удельный вес, скорость жидкости для левого и правого сечений равны
Если весовой расход в левом сечении участка трубки тока равен
Одновременно в единицу времени через правое сечение на из трубки тока удаляется энергия: При установившемся потоке невязкой жидкости полная энергия жидкости в участке трубки тока не изменяется, т.е.:
Учитывая, что, по уравнению неразрывности струи: получим окончательно математическую формулировку закона Бернулли: Физически закон Бернулли (уравнение Бернулли) имеет смысл закона сохранения энергии с учетом закона сохранения массы. ФОРМУЛА ТОРИЧЕЛЛИ
формула Торричелли позволяет определить скорость истечения жидкости из отверстия в сосуде. Предположим, что в широкий сосуд площади сечения S налита жидкость, свободная поверхность которой находится на высоте Z над центром малого отверстия площади в боковой стенке сосуда Давление на свободной поверхности жидкости н в вытекающей струе непосредственно за отверстием равно атмосферному Ра. Пусть скорость истечения жидкости равна Запишем уравнение Бернулли, сравнивая сечение для свободной поверхности жидкости с сечением отверстия:
Т.к. площадь сечения отверстия мала по сравнению с сечением сосуда, а жидкость несжимаема, то: откуда следует формула Торричелли:
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 246; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.42.247 (0.006 с.) |


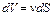


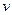 - скорость жидкости, r - плотность жидкости, g - удельный вес жидкости.
- скорость жидкости, r - плотность жидкости, g - удельный вес жидкости.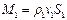







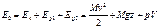
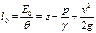

 и:
и: 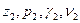
 , то в единицу времени в выделенный участок втекающей жидкостью вносится энергия:
, то в единицу времени в выделенный участок втекающей жидкостью вносится энергия:



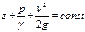

 , а скорость понижения уровня жидкости в сосуде -
, а скорость понижения уровня жидкости в сосуде -  . Жидкость будем считать несжимаемой.
. Жидкость будем считать несжимаемой.