Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поступательное движение твёрдого тела.Содержание книги
Поиск на нашем сайте
Поступательным называют такое движение твердого тела, при котором любая прямая, проведенная в теле, при движении тела остается параллельной самой себе
т.е. и скорости всех точек тела одинаковы. Аналогично можно показать, что и ускорения всех точек тела одинаковы. Следовательно, при поступательном движении все точки тела движутся одинаково и для описания движения тела достаточно рассмотреть движение только одной его точки (чаще всего центра масс тела). ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТЕЛ.
Вращательным называется такое движение твердого тела, при котором хотя бы две его точки остаются неподвижными в пространстве. Прямая, проходящая через неподвижные точки тела, называются осью вращения. При вращательном движении все точки тела движутся в параллельных плоскостях, описывая концентрические окружности, центры которых лежат на оси вращения. Быстрота вращения определяется угловой скоростью.
Средней угловой скоростью называют величину:
для определения w как вектора необходимо угол поворота (угловое перемещение) также определять как вектор. Вектором углового перемещения называют вектор, направленный вдоль оси вращения в ту сторону, откуда вращение тела видно происходящим против хода часовых стрелок. По такому определению вектор угловой скорости равен: В случае вращения тела, показанном на рис. 10, вектор угловой скорости направлен вверх вдоль оси вращения.
Вектором среднего углового ускорения называют вектор
Легко видеть, что при ускоренном вращении твердого тела вектор углового ускорения направлен вдоль оси вращения в ту же сторону, что и вектор угловой скорости, а при замедленном - вдоль оси вращения противоположно вектору угловой скорости. ДВИЖЕНИЕ ОТДЕЛЬНЫХ ТОЧЕК ВРАЩАЮЩЕГОСЯ ТВЕРДОГО ТЕЛА.
характеристики их движения (и) различаются. Предположим, что произвольная точка вращающегося тела находится на расстоянии г от оси вращения (рис.11).
За промежуток времени Dt проходит по своей траектории путь DS. Средняя скорость точки при этом равна: а мгновенная:
Ускорение отдельных точек вращающегося твердого тела удобно определять по отдельным его составляющим at, an:
Как видно из приведенных соотношений, полное ускорение и отдельные его составляющие зависят от расстояния r до оси вращения. Таким образом, угол отклонения вектора полного ускорения от радиуса вращения одинаков для всех точек тела. ПЛОСКОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА. Плоским называют такое движение тела, при котором все его точки движутся в плоскостях, параллельных заданной неподвижной.
Для определения положения сечения в пространстве в любой момент времени необходимо прежде всего задать положение произвольной точки А (полюса) этого сечения векторным или координатным способом. Кроме того, необходимо провести в сечении произвольную прямую АВ и указать угол a (альфа), который она образует с одной из осей координат (рис. 14). Движение сечения считается
или
Следовательно, и в этом случае плоское перемещение можно представить как одновременно происходящие поступательное перемещение вместе с полюсом и вращение вокруг него. Очевидно, что и направление, и угол поворота в обоих случаях совладают. Поэтому кинематические характеристики поступательной части движения зависят от выбора полюса, а вращательной - не зависят. Сила. Изменение состояния тела происходит в результате взаимодействий, которые приводят к изменению, как внутреннего состояния тел, так и состояния их движения. Количественной мерой взаимодействий, приводящих к изменению состояний тел, является сила. Сила - векторная величина, она характеризуется следующими элементами: величиной, направлением в пространстве и точкой приложения силы. Линия, вдоль которой направлена сила, называется линией действия силы. Совокупность сил, приложенных к телу, называют системой сил. Если под действием системы сил, приложенных к телу, оно может пребывать в состоянии покоя, система называется уравновешенной Сила, равная по величине равнодействующей и противоположно ей направленная, называется уравновешивающей. Силы взаимодействия между телами одной и той же системы называются внутренними. Силы взаимодействия с телами, не входящими в состав данной системы называются внешними. Силы, приложенные в одной точке тела, называются сосредоточенными. Силы, приложенные ко всем точкам поверхности или объема тела, называются распределенными.
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 280; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.176.111 (0.006 с.) |

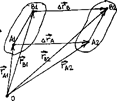
 Поэтому перемещения точек А и В равны (Dra = Drb) Поскольку точки выбирались произвольно, можно сделать вывод, что при поступательном движении тела все его точки совершают одинаковые перемещения. По определению:
Поэтому перемещения точек А и В равны (Dra = Drb) Поскольку точки выбирались произвольно, можно сделать вывод, что при поступательном движении тела все его точки совершают одинаковые перемещения. По определению: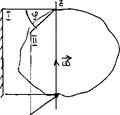

 а мгновенной:
а мгновенной:

 а мгновенного
а мгновенного
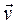

 Хотя все точки вращающегося тела имеют одинаковые и кинематические
Хотя все точки вращающегося тела имеют одинаковые и кинематические
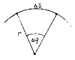

 С учетом направлений векторов угловой и линейной скорости, а также радиус-вектора рассматриваемой точки, получим:
С учетом направлений векторов угловой и линейной скорости, а также радиус-вектора рассматриваемой точки, получим:
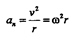
 Полное ускорение точки равно
Полное ускорение точки равно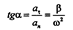



 заданным, если для любого момента времени известны зависимости:
заданным, если для любого момента времени известны зависимости: