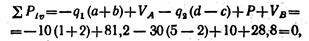Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 1.4. Балочные системы. Определение реакций опор и моментов защемленияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Иметь представление о видах опор и возникающих реакциях в опорах. Знать три формы уравнений равновесия и уметь их использовать для определения реакций в опорах балочных систем. Уметь выполнять проверку правильности решения. Виды нагрузок и разновидности опор Виды нагрузок
По способу приложения нагрузки делятся на · сосредоточенные и · распределенные. Если реально передача нагрузки происходит на пренебрежимо малой площадке (в точке), нагрузку называют сосредоточенной. Часто нагрузка распределена по значительной площадке или линии (давление воды на плотину, давление снега на крышу и т.п.), тогда нагрузку считают распределенной. В задачах статики для абсолютно твердых тел распределенную нагрузку можно заменить равнодействующей сосредоточенной силой (рис. 6.1).
q — интенсивность нагрузки; I — длина стержня; G = ql — равнодействующая распределенной нагрузки. Разновидности опор балочных систем (см. лекцию 1) Балка — конструктивная деталь в виде прямого бруса, закрепленная на опорах и изгибаемая приложенными к ней силами. Высота сечения балки незначительна по сравнению с длиной.
Жесткая заделка (защемление) (рис. 6.2)
Для определения этих неизвестных удобно использовать систему уравнений в виде
Каждое уравнение имеет одну неизвестную величину и решается без подстановок. Для контроля правильности решений используют дополнительное уравнение моментов относительно любой точки на балке, например
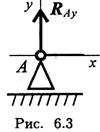
Шарнирно-подвижная опора (рис. 6.3) Опора допускает поворот вокруг шарнира и перемещение вдоль опорной поверхности. Реакция направлена перпендикулярно опорной поверхности. Шарнирно-неподвижная опора (рис. 6.4)
Опора допускает поворот вокруг шарнира и может быть заменена двумя составляющими силы вдоль осей координат.
Балка на двух шарнирных опорах (рис. 6.5)
Не известны три силы, две из них — вертикальные, следовательно, удобнее для определения неизвестных использовать систему уравнений во второй форме:
Составляются уравнения моментов относительно точек крепления балки. Поскольку момент силы, проходящей через точку крепления, равен 0, в уравнении останется одна неизвестная сила.
Для контроля правильности решения используется дополнительное уравнение
При равновесии твердого тела, где можно выбрать три точки, не лежащие на одной прямой, удобно использовать систему уравнений в третьей форме (рис. 6.6):
Примеры решения задач
Пример 1. Одноопорная (защемленная) балка нагружена сосредоточенными силами и парой сил (рис. 6.7). Определить реакции заделки.
Решение 2. В заделке может возникнуть реакция, представляемая двум: составляющими ( R Ay, R Ax), и реактивный момент МA. Наносим на схему балки возможные направления реакций. Замечание. Если направления выбраны неверно, при расчетах получим отрицательные значения реакций. В этом случае реакции на схеме следует направить в противоположную сторону, не повторяя расчета. В силу малой высоты считают, что все точки балки находятся на одной прямой; все три неизвестные реакции приложены в одной точке. Для решения удобно использовать систему уравнений равновесия в первой форме. Каждое уравнение будет содержать одну неизвестную.
3. Используем систему уравнений:
Знаки полученных реакций (+), следовательно, направления реакций выбраны верно. 3. Для проверки правильности решения составляем уравнение моментов относительно точки В.
Подставляем значения полученных реакций:
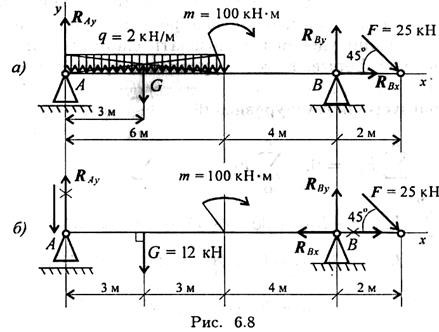
Решение выполнено верно. Пример 2. Двухопорная балка с шарнирными опорами А и В нагружена сосредоточенной силой F, распределенной нагрузкой с интенсивностью q и парой сил с моментом т (рис. 6.8а). Определить реакции опор.
Решение
1. Левая опора (точка А) — подвижный шарнир, здесь реакция направлена перпендикулярно опорной поверхности. Правая опора (точка В) — неподвижный шарнир, здесь наносим две составляющие реакции вдоль осей координат. Ось Ох совмещаем с продольной осью балки. 2. Поскольку на схеме возникнут две неизвестные вертикальные реакции, использовать первую форму уравнений равновесия нецелесообразно. 3. Заменяем распределенную нагрузку сосредоточенной: G = ql; G = 2*6 = 12 кН. Сосредоточенную силу помещаем в середине пролета, далее задача решается с сосредоточенными силами (рис. 6.8, б). 4. Наносим возможные реакции в опорах (направление произвольное). 5. Для решения выбираем уравнение равновесия в виде
6. Составляем уравнения моментов относительно точек крепления:
Реакция отрицательная, следовательно, R Аy нужно направить н противоположную сторону.
7. Используя уравнение проекций, получим:
RBx — горизонтальная реакция в опоре В. Реакция отрицательна, следовательно, на схеме ее направление будет противоположно выбранному.
8. Проверка правильности решения. Для этого используем четвертое уравнение равновесия
Подставим полученные значения реакций. Если условие выполнено, решение верно: -5,1 - 12 + 34,6 – 25 -0,7 = 0.
Решение
Рассмотрим равновесие балки АВ. Отбросим опорное закрепление (заделку) и заменим его действие реакциями НА, VA и тА (рис. 1.17, б). Получили плоскую систему произвольно расположенных сил. Выбираем систему координат (рис. 1.17,6) и составляем уравнения равновесия:
Составим проверочное уравнение
следовательно, реакции определены верно.
Решение
Рассматриваем равновесие балки АВ. Отбрасываем опорные закрепления и заменяем их действие реакциями (рис. 1.18,6). Получили плоскую систему произвольно расположенных сил.
Подставив числовые значения, получим
откуда VB = 28,8 кН;
Подставив числовые значения, получим:
откуда VA = 81,2 кН. Составляем проверочное уравнение:
следовательно, опорные реакции определены верно.
Пример 5. Для заданной стержневой системы (рис. 1.19, а) определить усилия в стержнях.
Решение
Рассмотрим равновесие балки AB, к которой приложены как заданные, так и искомые силы. На балку действуют равномерно распределенная нагрузка интенсивностью q, сила Р и сосредоточенный момент т. Освободим балку от связей и заменим их действие реакциями (рис. 1.19, б). Получили плоскую систему произвольно расположенных сил. Выбираем систему координат (см. рис. 1.19, б) и составляем уравнения равновесия:
равномерно распределенной нагрузки интенсивностью q (на чертеже она показана штриховой линией). Подставив числовые значения, получим:
откуда NAC = 16 кН;
Напомним, что сумма проекций сил, образующих пару, на любую ось равна нулю;
где NBD cos α — вертикальная составляющая силы NBD', NBFcos β — вертикальная составляющая силы N B F (линии действия горизонтальных составляющих сил NBD и NBF проходят через точку А и поэтому их моменты относительно точки А равны нулю). Подставляя числовые значения и учитывая, что N B D = 1,41 NBF, получаем:
откуда N B F = 33,1 кН. Тогда NBD = 1,41*33,1 = 46,7 кН. Для определения усилий в стержнях не было использовано уравнение равновесия: ΣPto= 0. Если усилия в стержнях определены верно, то сумма проекций на ось v всех сил, действующих на балку, должна быть равна нулю. Проектируя все силы на ось v, получаем:
следовательно, усилия в стержнях определены верно.
Пример 6. Для заданной плоской рамы (рис. 1.20, а) определить опорные реакции
Решение
Освобождаем раму от связей и заменяем их действие реакциями NА, VA, VB (рис. 1.20, б). Получили плоскую систему произвольно расположенных сил.
где Р2 cos α — вертикальная составляющая силы Р2; P2 sin α — горизонтальная составляющая силы Р2; 2qa — равнодействующая равномерно распределенной нагрузки интенсивностью q (показана штриховой линией);
откуда VB = 5,27 qa;
или
откуда HA=7qa
линия действия силы Р2 cos α проходит через точку В и поэтому ее момент относительно точки В равен нулю
откуда VA = 7qa. Для определения реакций не было использовано уравнение равновесия Σ Piv=0. Если реакции определены верно, то сумма проекций на ось v всех сил, действующих на раму, должна быть равна нулю. Проектируя все силы на ось v, получаем:
следовательно, опорные реакции определены верно. Напомним, что сумма проекций сил, составляющих пару с моментом т, на любую ось равна нулю. Контрольные вопросы и задания
1. Замените распределенную нагрузку сосредоточенной и определите расстояние от точки приложения равнодействующей до опоры А (рис. 6.9).
2. Рассчитайте величину суммарного момента сил системы относительно точки А (рис. 6.10).
3. Какую из форм уравнений равновесия целесообразно использовать при определении реакций в заделке? 4. Какую форму системы уравнений равновесия целесообразно использовать при определении реакций в опорах двухопорной балки и почему?
5. Определите реактивный момент в заделке одноопорной балки, изображенной на схеме (рис. 6.11).
6. Определите вертикальную реакцию в заделке для балки, представленной на рис. 6.11.
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 101786; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.140.152 (0.008 с.) |


 Опора не допускает перемещений и поворотов. Заделку заменяют двумя составляющими силы Rax и и парой с моментом Mr.
Опора не допускает перемещений и поворотов. Заделку заменяют двумя составляющими силы Rax и и парой с моментом Mr.















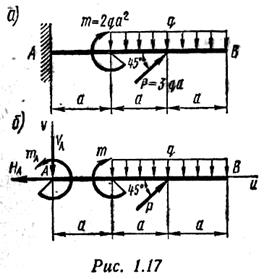 Пример 3. Определить опорные реакции балки, показанной на рис. 1.17, а.
Пример 3. Определить опорные реакции балки, показанной на рис. 1.17, а.

 Пример 4. Для заданной балки (рис. 1.18, а) определить опорные реакции.
Пример 4. Для заданной балки (рис. 1.18, а) определить опорные реакции.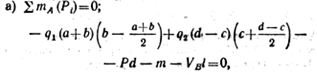
 равнодействующая равномерно распределенной нагрузки интенсивностью q1,
равнодействующая равномерно распределенной нагрузки интенсивностью q1, расстояние от точки А до линии действия равнодействующей q1(а + b);
расстояние от точки А до линии действия равнодействующей q1(а + b); равнодействующая равномерно распределенной нагрузки интенсивностью q2;
равнодействующая равномерно распределенной нагрузки интенсивностью q2; расстояние от точки А до линии действия равнодействующей q2 (d — с).
расстояние от точки А до линии действия равнодействующей q2 (d — с).

 — расстояние от точки В до линии действия равнодействующей q1 (a+b);
— расстояние от точки В до линии действия равнодействующей q1 (a+b); — расстояние от точки В до линии действия равнодействующей q2(d — c).
— расстояние от точки В до линии действия равнодействующей q2(d — c).