
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Плоскопараллельное движение телаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Пример 6. Зубчатое колесо зажато между двумя параллельными зубчатыми рейками (рис. 1.51, а). Нижняя рейка неподвижна, верхняя — движется со скоростью v = 4 м/с. Определить скорость точки В. Решение
Тогда скорость точки В можно рассматривать как геометрическую сумму скоростей в поступательном (переносном) и во вращательном (относительном) движениях (рис. 1.51, б):
где
Как известно, угловая скорость относительного вращательного движения не зависит от выбора полюса, поэтому, приняв за полюс точку Р (рис. 1.51, б), найдем
Скорость точки А — общей точки колеса и рейки vA = 4 м/с. Очевидно, Модуль скорости точки В
Решим пример другим способом. Движение колеса можно рассматривать в любой момент времени как вращательное вокруг мгновенного центра вращения. В рассматриваемом примере мгновенный центр вращения колеса — точки касания колеса с неподвижной рейкой (точка Р). Скорость точки А можно определить как скорость во вращательном движении вокруг точки Р:
откуда
т. е.
Тогда
Решение По заданному закону движения точки О определяем ее скорость в момент времени t = 2 с:
при t = 2 с v 0 = 9 м/с. Цилиндр совершает плоскопараллельное движение. Мгновенный центр вращения находится в точке Р. Поэтому
Отсюда мгновенная угловая скорость вращения цилиндра
Найдем расстояния от мгновенного центра скоростей Р до заданных точек:
Для определения расстояния РН рассмотрим прямоугольные треугольники НКО и РКН. Из треугольника НКО имеем
Теперь определим величины скоростей заданных точек:
Вектора скоростей показаны на рис. 1.52. Пример 8. В механизме грохота (рис. 1.53, а) кривошипы O1А и O2В связаны звеном АВ. Размеры всех звеньев одинаковы: O1А = O2В = АВ = 40 см. Кривошип O1A равномерно вращается вокруг оси Ох с частотой п о = 60 об/мин. Определить угловую скорость звена АВ и скорость точки В для двух положений грохота: 1) когда кривошип O1A занимает горизонтальное положение, 2) когда кривошип O2В занимает горизонтальное положение.
Вычислим скорость точки А ведущего кривошипа:
Рассмотрим теперь последовательно заданные положения механизма. 1-е положение (рис. 1.53, б). При заданных размерах звеньев угол АВО2 = 90°. Определим мгновенный центр вращения звена АВ. Нам известны направления скоростей двух его точек: vA и vB. Мгновенный центр скоростей лежит на пересечении перпендикуляров к направлениям скоростей vA и vB, т. е. в точке О2. Найдем мгновенную угловую скорость вращения звена АВ:
откуда
Определяем скорость точки В: 2-е положение (рис. 1.53, в). Мгновенный центр скоростей в этом положении находится в точке Ov. Мгновенная угловая скорость вращения звена АВ оказывается равной угловой скорости ведущего кривошипа механизма:
Определяем скорость точки В:
Пример 9. Железнодорожный вагон движется по горизонтальному участку с ускорением а0 = — 1,6 м/с2, имея в данный момент скорость v 0 = 1 м/с. Найти ускорения точек вагонного колеса, лежащих на концах горизонтального и вертикального диаметров (рис. 1.54). Решение
Движение центра колеса О примем за переносное ае = а0. Относительное движение является вращательным относительно выбранного полюса О. Найдем угловую скорость и угловое ускорение относительного движения.
Рассматривая движение точки О относительно мгновенного центра скоростей, который совпадает с точкой Р, найдем угловую скорость вращения колеса: ω = v0/OP = v0/R = 1/0,4 = 2,5 рад/с. Как известно, v = ωR. Продифференцируем полученное уравнение по времени:
Следовательно, at = Rε. В рассматриваемом примере at — касательное ускорение точки О в поступательном движении, т. е. at = — a0 (движение замедленное), ε — угловое ускорение колеса во вращательном движении вокруг точки О. Тогда
Поскольку все исследуемые точки А, В, Р и С находятся на одинаковом расстоянии от центра колеса, то относительные касательные и нормальные ускорения их по величине соответственно одинаковы и определяются по формулам:
На рис. 1.54 в каждой точке построены три составляющих ускорения:
Два из трех составляющих векторов для каждой точки направлены по одной прямой и складываются алгебраически. Векторные построения, выполненные на рис. 1.54 около точек А, В и Р, позволяют найти величины и направления их абсолютных ускорений:
Контрольные вопросы и задания
Темы 1.10, 1.11. Кинематика. Сложное движение точки. Сложное движение твердого тела
ЛЕКЦИЯ 13 Тема 1.12. Основные понятия и аксиомы динамики. Понятие о трении Иметь представление о массе тела и ускорении свободного падения, о связи между силовыми и кинематическими параметрами движения, о двух основных задачах динамики. Знать аксиомы динамики и математическое выражение основного закона динамики. Знать зависимости для определения силы трения. Содержание и задачи динамики
Динамика — раздел теоретической механики, в котором устанавливается связь между движением тел и действующими на них силами. В динамике решают два типа задач:
При поступательном движении все точки тела движутся одинаково, поэтому тело можно принять за материальную точку. Если размеры тела малы по сравнению с траекторией, его тоже можно рассматривать как материальную точку, при этом точка совпадает с центром тяжести тела. При вращательном движении тела точки могут двигаться неодинаково, в этом случае некоторые положения динамики можно применять только к отдельным точкам, а материальный объект рассматривать как совокупность материальных точек. Поэтому динамику делят на динамику точки и динамику материальной системы. Аксиомы динамики Законы динамики обобщают результаты многочисленных опытов и наблюдений. Законы динамики, которые принято рассматривать как аксиомы, были сформулированы Ньютоном, но первый и четвертый законы были известны Галилею. Механику, основанную на этих законах, называют классической механикой. Первая аксиома (принцип инерции): Всякая изолированная материальная точка находится в состоянии покоя или равномерного и прямолинейного движения, пока приложенные силы не выведут ее из этого состояния. Это состояние называют состоянием инерции. Вывести точку из этого состояния, т. е. сообщить ей некоторое ускорение, может внешняя сила. Всякое тело (точка) обладает инертностью. Мерой инертности является масса тела. Массой называют количество вещества в объеме тела, в классической механике ее считают величиной постоянной. Единица измерения массы — килограмм (кг). Вторая аксиома (второй закон Ньютона — основной закон динамики) Зависимость между силой, действующей на материальную точку, и сообщаемым ею ускорением следующая: F = та, где т — масса точки, кг; а — ускорение точки, м/с2. Ускорение, сообщенное материальной точке силой, пропорционально величине силы и совпадает с направлением силы.
Основной закон динамики в дифференциальной форме:
На все тела на Земле действует сила тяжести, она сообщает телу ускорение свободного падения, направленное к центру Земли: G = тg,
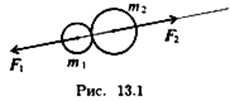
Третья аксиома (третий закон Ньютона). Силы взаимодействия двух тел равны по величине и направлены по одной прямой в разные стороны (рис. 13.1):
Откуда
При взаимодействии ускорения обратно пропорциональны массам. Четвертая аксиома (закон независимости действия сил).
|
|||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 1779; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.01 с.) |

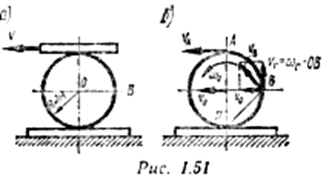 Колесо совершает плоскопараллельное движение. Как известно, плоскопараллельное движение можно представить как сумму двух движении: поступательного вместе с осью О и вращательного вокруг той же оси.
Колесо совершает плоскопараллельное движение. Как известно, плоскопараллельное движение можно представить как сумму двух движении: поступательного вместе с осью О и вращательного вокруг той же оси.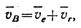
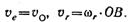
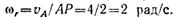






 Пример 7. Цилиндр с выступающим ободом катится без скольжения по горизонтальной поверхности (рис. 1.52). При этом центр цилиндра — точка О движется прямолинейно от начального положения Ох согласно уравнению s = 0,75 t 3 (s — в метрах, t — в секундах). Определить скорости точек В и С цилиндра, а также точек А, Е, F и Н, лежащих на ободе цилиндра в момент времени t = 2 с. Диаметр цилиндра d = 1 м, обода D = 1,8 м.
Пример 7. Цилиндр с выступающим ободом катится без скольжения по горизонтальной поверхности (рис. 1.52). При этом центр цилиндра — точка О движется прямолинейно от начального положения Ох согласно уравнению s = 0,75 t 3 (s — в метрах, t — в секундах). Определить скорости точек В и С цилиндра, а также точек А, Е, F и Н, лежащих на ободе цилиндра в момент времени t = 2 с. Диаметр цилиндра d = 1 м, обода D = 1,8 м.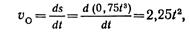



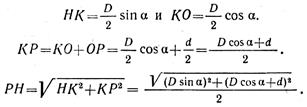

 Решение
Решение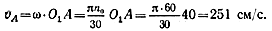



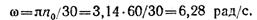
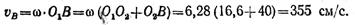
 Составим выражение скорости точки О в произвольный момент времени:
Составим выражение скорости точки О в произвольный момент времени: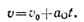

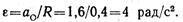
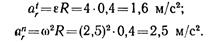




 где g = 9,81м/с2, ускорение свободного падения.
где g = 9,81м/с2, ускорение свободного падения.




