
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Пространственная сходящаяся система силСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Пространственная сходящаяся система сил — система сил, не лежащих в одной плоскости, линии действия которых пересекаются в одной точке. Равнодействующую пространственной системы сил можно определить, построив пространственный многоугольник (рис. 7.3),
Доказано, что равнодействующая системы сходящихся сил приложена в точке пересечения линий действия сил системы. Модуль равнодействующей пространственной системы сходящихся сил можно определить аналитически, использовав метод проекций.
Совмещаем начало координат с точкой пересечения линий действия сил системы. Проецируем все силы на оси координат и суммируем соответствующие проекции (рис. 7.4). Получим проекции равнодействующей на оси координат:
Модуль равнодействующей системы сходящихся сил определим по формуле
Направление вектора равнодействующей определяется углами
Произвольная пространственная система сил Приведение произвольной пространственной системы сил к центру О. Дана пространственная система сил (рис. 7.5, а). Приведем ее к центру О. Силы необходимо параллельно перемещать, при этом образуется система пар сил. Момент каждой из этих пар равен произведению модуля силы на расстояние до центра приведения. В центре приведения возникает пучок сил, который может быть заменен суммарной силой (главный вектор) FГЛ (рис. 7.5, б). Моменты пар сил можно сложить, получив суммарный момент системы Мгл (главный момент).
Главный вектор принято раскладывать на три составляющие, направленные вдоль осей координат (рис. 7.5, в). Обычно суммарный момент раскладывают на составляющие: три момента относительно осей координат. Абсолютное значение главного вектора (рис. 7.5б) равно
Абсолютное значение главного момента определяется по формуле.
Уравнения равновесия пространственной системы сил При равновесии F гл = 0; Мгл = 0. Получаем шесть уравнений равновесия:
Шесть уравнений равновесия пространственной системы сил соответствуют шести независимым возможным перемещениям тела в пространстве: трем перемещениям вдоль координатных осей и трем вращениям вокруг этих осей. Примеры решения задач
Решение 1. Моменты сил относительно оси Ох:
2. Моменты сил относительно оси Оу.
Пример 2. На горизонтальном валу закреплены два колеса, г1 = 0,4 м; г2 = 0,8 м. Остальные размеры — на рис. 7.7. К колесу 1 приложена сила F1, к колесу 2 — силы F2 = 12 кН, F3 = 4кН. Определить силу F1 и реакции в шарнирах А и В в состоянии равновесия. Напомним: 1. При равновесии выполняются шесть уравнений равновесия. Уравнения моментов следует составлять относительно опор А и В. 2. Силы F 2 \\O x; F 2\\Oy; F 3\\Oy. Моменты этих сил относительно соответствующих осей равны нулю. 3. Решение 1. Определяем силу F\, составив уравнение моментов сил относительно оси Oz:
2. Определяем реакции в опоре А. На опоре действуют две составляющие реакции (YA; XA). Составляем уравнение моментов сил относительно оси Ох' (в опоре В). Поворот вокруг оси Ох' не происходит:
Знак «минус» означает, что реакция направлена в противоположную сторону. Поворот вокруг оси Оу' не происходит, составляем уравнение моментов сил относительно оси Оу' (в опоре В):
3.Определяем реакции в опоре В. На опоре действуют две составляющие реакции (XB, YB). Составляем уравнение моментов сил относительно оси Ох (опора А):
Составляем уравнение моментов относительно оси Оу (опора А):
4.Проверка. Используем уравнения проекций:
Расчёт выполнен верно.
Пример 3. Определить численное значение силы P1, при котором вал ВС (рис. 1.21, а) будет находиться в равновесии. При найденном значении силы Р1 определить опорные реакции.
Решение
Опоры вала, изображенные на рис. 1.21, а, надо рассматривать как пространственные шарнирные опоры, препятствующие линейным перемещениям в направлениях осей и и v (выбранная система координат показана на рис. 1.21, б). Освобождаем вал от связей и заменяем их действие реакциями VВ, НВ, VC, НС (рис. 1.21, б). Получили пространственную систему сил, для которой составляем уравнения равновесия, пользуясь выбранной системой координат (рис. 1.21,6):
где А1 *1,25D/2 — момент относительно оси и силы A1, приложенной к правому зубчатому колесу. Моменты относительно оси и сил Т1 и А1 (приложенных к среднему зубчатому колесу), Р1 (приложенной к правому зубчатому колесу) и Р равны нулю, так как силы Р, T1, Р1 параллельны оси и, а сила А1 пересекает ось и.
откуда VС = 0,37P;
или
откуда VB=0,37P. Составим проверочное уравнение:
следовательно, реакции VB и VС определены верно;
где А1* 1 ,25D/2 — момент относительно оси v силы А1, приложенной к среднему зубчатому колесу. Моменты относительно оси v сил Т, Р1 (приложенной к среднему зубчатому колесу), А1 и Т1 (приложенных к правому зубчатому колесу) равны нулю, так как силы Т, Р1, Т1 параллельны оси v, сила А1 пересекает ось v.
откуда HC = 0,81Р;
или
откуда HС = 1,274Р Составим проверочное уравнение:
следовательно, реакции НВ и НС определены верно. В заключение отметим, что опорные реакции получились со знаком плюс. Это указывает на то, что выбранные направления VB, НВ, VC и НС совпадают с действительными направлениями реакций связей.
Определить натяжения ветвей ременной передачи и реакции подшипников А и В, пренебрегая массой вала.
Решение
Рассматриваем равновесие горизонтального коленчатого вала со шкивом. Прикладываем в соответствии с условием задачи заданные силы Р, S1, S2 и G. Освобождаем вал от опорных закреплений и заменяем их действие реакциями VA, НА, VB и НВ. Координатные оси выбираем так, как показано на рис. 1.22. В шарнирах А и В не возникает реакций вдоль оси w, так как натяжение ветвей ремня и все остальные силы действуют в плоскостях, перпендикулярных этой оси. Составим уравнения равновесия:
Кроме того, по условию задачи имеем еще одно уравнение
Таким образом, здесь имеется шесть неизвестных усилий S1, S2, НА, VA, НВ и VB и шесть связывающих их уравнений. Уравнение проекций на ось w в рассматриваемом примере обращается в тождество 0 = 0, так как все силы лежат в плоскостях, перпендикулярных оси w. Подставляя в уравнения равновесия S1=2S2 и решая их, находим:
Значение реакции НВ получилось со знаком минус. Это значит, что в действительности ее направление противоположно принятому на рис. 1.22. Контрольные вопросы и задания
1. Запишите формулы для расчета главного вектора пространственной системы сходящихся сил. 2. Запишите формулу для расчета главного вектора пространственной системы произвольно расположенных сил. 3. Запишите формулу для расчета главного момента пространственной системы сил. 4. Запишите систему уравнений равновесия пространственной системы сил. 5. Какое из уравнений равновесия нужно использовать для определения реакции стержня R1 (рис. 7.8)?
6. Определите главный момент системы сил (рис. 7.9). Точка приведения — начало координат. Координатные оси совпадают с ребрами куба, ребро куба равно 20 см; F 1 — 20кН; F 2 — 30кН. 7. Определите реакцию Хв (рис. 7.10). Вертикальная ось со шкивом нагружена двумя горизонтальными силами. Силы F1 и F2 параллельны оси Ох. АО = 0,3 м; ОВ = 0,5 м; F1 = 2кН; F2 = 3,5 кН.
Рекомендация. Составить уравнение моментов относительно оси Оу' в точке А. 8. Ответьте на вопросы тестового задания.
|
||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 8187; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.01 с.) |





 Таким образом, произвольная пространственная система сил приводится к главному вектору и главному моменту.
Таким образом, произвольная пространственная система сил приводится к главному вектору и главному моменту.





 Пример 1. На тело в форме куба с ребром а = 10 см действуют три силы (рис. 7.6). Определить моменты сил относительно осей координат, совпадающих с ребрами куба.
Пример 1. На тело в форме куба с ребром а = 10 см действуют три силы (рис. 7.6). Определить моменты сил относительно осей координат, совпадающих с ребрами куба.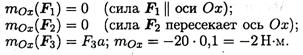

 Расчет следует завершить проверкой, использовав дополнительные уравнения равновесия.
Расчет следует завершить проверкой, использовав дополнительные уравнения равновесия.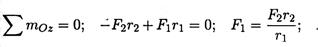




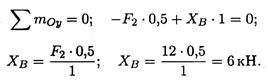

 Действующие на зубчатые колеса силы Р и Р1 направлены по касательным к начальным окружностям колес; силы Т и Т1 — по радиусам колес; силы А1 параллельны оси вала. Т = 0,36Р, 7Т1 = Р1; А1 = 0,12P1.
Действующие на зубчатые колеса силы Р и Р1 направлены по касательным к начальным окружностям колес; силы Т и Т1 — по радиусам колес; силы А1 параллельны оси вала. Т = 0,36Р, 7Т1 = Р1; А1 = 0,12P1.






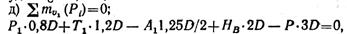
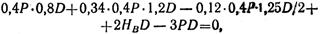
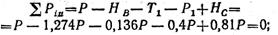
 Пример 4. Сила давления шатуна парового двигателя Р = 25 кН передается на середину шейки коленчатого вала в точке D под углом α = 30° к горизонту при вертикальном расположении щек колена (рис. 1.22). На конец вала насажен шкив ременной передачи. Натяжение ведущей ветви ремня в два раза больше, чем ведомой, т.е. S1 = 2S2. Сила тяжести маховика G = 10 кН.
Пример 4. Сила давления шатуна парового двигателя Р = 25 кН передается на середину шейки коленчатого вала в точке D под углом α = 30° к горизонту при вертикальном расположении щек колена (рис. 1.22). На конец вала насажен шкив ременной передачи. Натяжение ведущей ветви ремня в два раза больше, чем ведомой, т.е. S1 = 2S2. Сила тяжести маховика G = 10 кН.







