
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основное уравнение динамики при поступательном движении телаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Для определения движения тела (системы материальных точек) можно использовать второй закон динамики
где т — суммарная масса тела; ас — ускорение центра масс тела. В поле земного притяжения центр масс совпадает с центром тяжести.
Пусть твердое тело под действием внешних сил вращается вокруг оси Oz с угловой скоростью ω (рис. 17.3). Рассматривая твердое тело как механическую систему, разобьем ее на множество материальных точек с массами Δmk. Каждая точка движется по окружности радиуса rk c касательным ускорением аkt = εrk и нормальным ускорением
Используем для каждой точки принцип Даламбера и приложим силы инерции:
Система сил, действующих на точку, по принципу Даламбера, находится в равновесии. Поэтому алгебраическая сумма моментов относительно оси вращения должна быть равна нулю:
где Mz — момент внешних сил. Моменты нормальных сил инерции Fинkn равны нулю, т. к. силы пересекают ось z. Силы, направленные по касательной к окружности, равны
где ε — общая величина, угловое ускорение тела. Подставив значение силы в формулу для определения моментов, получим
Величина
называется моментом инерции тела относительно оси вращения и обозначается
В результате получим выражение основного уравнения динамики вращающего тела:
где Mz — сумма моментов внешних сил относительно оси; ε — угловое ускорение тела.
Момент инерции тела в этом выражении определяет меру инертности тела при вращении. По выражению для момента инерции можно определить, что единица измерения этой величины в системе СИ [Jz\ = [тг2] = кг-м2. Видно, что значение момента инерции зависит от распределения массы относительно оси вращения: при одинаковой массе момент инерции больше, если основная часть массы расположена дальше от оси вращения. Для увеличения момента инерции используют колеса со спицами и отверстиями.
Моменты инерции некоторых тел Момент инерции сплошного цилиндра (рис. 17.4)
Момент инерции полого тонкостенного цилиндра (рис. 17.5)
Момент инерции прямого тонкого стержня любого поперечного сечения
Момент инерции шара (рис. 17.7)
Примеры решения задач
Пример 1. Автомобиль двигался со скоростью 54 км/ч. В результате резкого торможения автомобиль остановился. Определите время торможения, если коэффициент трения между поверхностью дороги и колесами автомобиля 0,36. Решение Принимаем автомобиль за материальную точку (рис. 17.8).
По теореме изменения количества движения
Конечная скорость v = 0 (остановка).
здесь R — сила прижатия; f — коэффициент трения; G — сила тяжести; т — масса автомобиля; g — ускорение свободного падения; g = 9,81м/с2.
Решение
где M∑ — суммарный момент внешних сил; J — момент инерции; ε — угловое ускорение; Мдв — движущий момент; Мхр — момент трения (сил сопротивления).
Тогда
3. Определим момент инерции колеса, считая его сплошным цилиндром:
4. Определяем величину тсгомозного момента — момента трения в подшипниках:
Решение 1. Используем основное уравнение динамики
2. Определяем суммарный момент внешних сил
Рассчитываем момент инерции шкива, влиянием вала пренебрегаем:
Определяем угловое ускорение шкива
Решение
Так как в число данных и искомых величин входят действующие силы (постоянные по величине и направлению), время движения, начальная и конечная скорости, то применяем теорему об изменении количества движения точки. Силы, действующие на точку в произвольном положении, показаны на рис. 1.67 Вычисляем проекции на ось х импульсов сил, действующих на тело:
(так как силы О и N перпендикулярны к оси х),
Составляем уравнение изменения количества движения
откуда
Пример 5. По наклонной плоскости с углом α = 30° опускается без начальной скорости тяжелое тело; коэффициент трения равен 0,1. Какую скорость будет иметь тело, пройдя 2 м от начала движения?
Так как в число данных и искомых величин входят действующие силы (постоянные по величине и направлению), перемещение точки, начальная и конечная скорости, то применим теорему об изменении кинетической энергии точки. Силы, действующие на тело в произвольном положении, показаны на рис. 1.68 (G — сила тяжести тела, N — реакция плоскости, Ттр — сила трения). Вычислим работы сил, действующих на тело:
(так как N и G1 перпендикулярны к перемещению точки их приложения). Составляем уравнение изменения кинетической энергии:
Так как тело опускается без начальной скорости, то v о = 0, тогда
откуда
Пример 6. Поезд массой т — 3-106 кг движется по прямолинейному участку пути со скоростью 20 м/с. Тормозной путь составляет 500 м. Определить время и силу торможения, считая ее постоянной. Решение
В число данных и искомых величин входят действующие силы (постоянные по величине и направлению), время движения, перемещение точки, начальная и конечная скорости, поэтому нужно применить теоремы об изменении количества движения и об изменении кинетической энергии точки. Силы, действующие на точку в произвольном положении, показаны на рис. 1.69 (Р — вес поезда, N — реакция рельсов, Ртo р — сила торможения). Для определения Ртo р применяем теорему об изменении кинетической энергии точки. Вычисляем работы сил, действующих на точку:
(так как силы Р и N перпендикулярны к направлению перемещения точки их приложения),
Составляем уравнение изменения кинетической энергии:
где
откуда
Для определения времени торможения применяем теорему, об изменении количества движения точки. Вычисляем проекции импульсов сил, действующих на точку:
(так как силы Р и N перпендикулярны к оси х),
Составляем уравнение изменения количества движения:
так как
откуда
Пример 7. Груз А массой 3 т и груз В массой т соединены нерастяжимой нитью, перекинутой через блок (рис. 1.70, а). Момент инерции блока относительно оси вращения
где D — диаметр блока. Коэффициент трения между поверхностями скольжения f = 0,1. Движение системы начинается из состояния покоя. Определить скорость груза В и угловую скорость блока после того, как груз В опустится на расстояние h. Массой нити и трением в блоке пренебречь. Решение
Система состоит из грузов А, В, нити и блока. В число данных и искомых величин входят: действующие силы (постоянные пo величине и направлению), перемещение системы, скорости тел в начале и в конце перемещения. Поэтому для решения задачи применяем теорему об изменении кинетической энергии системы.
Так как система вначале находилась в покое, то ее начальная кинетическая энергия Т0 равна нулю. Кинетическая энергия Т1 системы при движении груза складывается из кинетической энергии Т1A груза A, кинетической энергии Т1Б груза В, кинетической энергии Т1бл блока. Вычислим кинетическую энергию системы в момент, когда груз опустится на расстояние h:
где
Выразив угловую скорость блока через скорость груза
Вычислим работу сил, приложенных к системе. Работа силы тяжести груза В равна Рh = тgh, работы сил N и 3 Р равны нулю (силы перпендикулярны перемещению точки их приложения), работа силы трения равна Сила натяжения нити является внутренней силой, поэтому ее работа равна нулю. Таким образом, уравнение кинетической энергии системы в данном случае имеет вид
Отсюда искомая скорость груза
Угловая скорость блока
Решение
Для решения задачи используем основное уравнение вращательного движения тела:
Угловое ускорение ротора
где J — момент инерции ротора;
Так как ротор вращается равномерно-ускоренно, то уравнение движения имеет вид:
(ротор начинает движение из состояния покоя). Подставив значение t = 6 с, получим
Число оборотов ротора
При равномерно-ускоренном вращательном движении угловая скорость вычисляется по формуле: При
Контрольные вопросы и задания
1. Тело массой 10 кг поднято на высоту 6 м. Определите потенциальную энергию тела и работу, которую совершит тело при падении с этой высоты. 2. Материальная точка массой 16 кг, движущаяся со скоростью 10 м/с, остановилась через 40 с. Определите величину тормозной силы. 3. 4. Сплошной однородный цилиндр вращается вокруг продольной оси (рис. 17.11). От каких параметров зависит момент инерции цилиндра? Варианты ответов: · Только от т. · От m и d. · От l, т и d. · От l и т.
5. Определите вращающий момент на шкиве (рис. 17.12); d — 60 мм. 6. По результату решения предыдущей задачи (вопрос 5) определите момент инерции шкива, если, двигаясь из состояния покоя, он приобрел угловую скорость 50 рад/с за 10 с. Примечание. При ответах на контрольные вопросы ускорение свободного падения можно принимать равным 10 м/с2.
|
||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 2190; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.01 с.) |


 Основное уравнение динамики вращающегося тела
Основное уравнение динамики вращающегося тела где ε — угловое ускорение.
где ε — угловое ускорение.



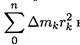











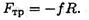



 Пример 2. После отключения двигателя колесо радиусом 0,5 м и массой 700 кг имело угловую частоту вращения 300 об/мин. Определите момент трения в подшипниках, если вал колеса остановился через 1,5 мин. Вращение принять равнопеременным, колесо считать сплошным цилиндром (рис. 17.9).
Пример 2. После отключения двигателя колесо радиусом 0,5 м и массой 700 кг имело угловую частоту вращения 300 об/мин. Определите момент трения в подшипниках, если вал колеса остановился через 1,5 мин. Вращение принять равнопеременным, колесо считать сплошным цилиндром (рис. 17.9).


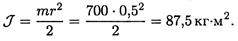


 Пример 3. Шкив приводится во вращение ременной передачей (рис. 17.10). Натяжение ведущей ветви ремня S1 = 120 Н, ведомой — S2 = 50 Н. Масса шкива 200 кг, диаметр 80 мм, момент сопротивления в подшипниках 1,2 Н-м. Определить угловое ускорение вала, пренебрегая его массой. Шкив считать тонкостенным цилиндром.
Пример 3. Шкив приводится во вращение ременной передачей (рис. 17.10). Натяжение ведущей ветви ремня S1 = 120 Н, ведомой — S2 = 50 Н. Масса шкива 200 кг, диаметр 80 мм, момент сопротивления в подшипниках 1,2 Н-м. Определить угловое ускорение вала, пренебрегая его массой. Шкив считать тонкостенным цилиндром.



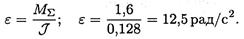
 Пример 4. Определить величину силы P, под действием которой тело массой т = 120 кг за t = 5 с приобретает скорость v = 500 м/с. Трением пренебречь.
Пример 4. Определить величину силы P, под действием которой тело массой т = 120 кг за t = 5 с приобретает скорость v = 500 м/с. Трением пренебречь. — сила тяжести тела, N — реакция поверхности, Р — движущая сила).
— сила тяжести тела, N — реакция поверхности, Р — движущая сила).
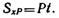



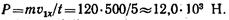
 Решение
Решение
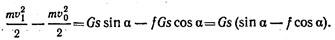





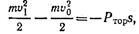
 Тогда
Тогда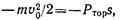








 Система в произвольном положении и действующие на нее силы показаны на рис. 1.70, б.
Система в произвольном положении и действующие на нее силы показаны на рис. 1.70, б.

 получим
получим




 Пример 8. В период пуска электродвигателя его ротор вращается под действием постоянного момента М1 = 80 Н-м. В подшипниках возникает момент сил трения М2 = 5 Н-м (рис. 1.71). Считая ротор однородным диском массой т = 100 кг, определить, сколько оборотов сделает ротор за 6 с после начала движения, и угловую скорость ротора в конце 10-й секунды.
Пример 8. В период пуска электродвигателя его ротор вращается под действием постоянного момента М1 = 80 Н-м. В подшипниках возникает момент сил трения М2 = 5 Н-м (рис. 1.71). Считая ротор однородным диском массой т = 100 кг, определить, сколько оборотов сделает ротор за 6 с после начала движения, и угловую скорость ротора в конце 10-й секунды.





 (в начальный момент М0 = 0).
(в начальный момент М0 = 0).

 Тело массой 9,2 кг двигалось из состояния покоя 3 с с ускорением 4 м/с2 под действием силы F. Определите запас кинетической энергии, накопленный телом.
Тело массой 9,2 кг двигалось из состояния покоя 3 с с ускорением 4 м/с2 под действием силы F. Определите запас кинетической энергии, накопленный телом.


