Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Темы 1. 12, 1. 13. Динамика. Движение материальной точки. Метод кинетостатики.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ЛЕКЦИЯ 15 Тема 1.14. Работа и мощность
Иметь представление о работе силы при прямолинейном и криволинейном перемещениях, о мощности полезной и затраченной, о коэффициенте полезного действия. Знать зависимости для определения силы трения, формулы для расчета работы и мощности при поступательном и вращательном движениях. Уметь рассчитывать работу и мощность с учетом потерь на трение и сил инерции. Работа
Для характеристики действия силы на некотором перемещении точки ее приложения вводят понятие «работа силы». Работа служит мерой действия силы, работа — скалярная величина. Работа постоянной силы на прямолинейном пути
Единицы измерения работы: 1 Дж (джоуль)= 1 Н-м; 1 кДж (килоджоуль) = 103 Дж. Рассмотрим частные случаи.
1. Силы, совпадающие с направлением перемещения, называются движущими силами. Направление вектора силы совпадает с направлением перемещения (рис. 15.2). В этом случае α = 0° (cos α = 1). Тогда W = FS > 0.
2. Силы, перпендикулярные направлению перемещения, работы не производят (рис. 15.3). Сила F перпендикулярна направлению перемещения, α = 90° (cos α = 0); W = 0.
3. Силы, направленные в обратную от направления перемещения сторону, называются силами сопротивления (рис. 15.4). Сила F направлена в обратную от перемещения S сторону. В этом случае α = 180° (cos α = — 1), следовательно, W = — FS < 0.
Движущие силы увеличивают модуль скорости, силы сопротивления уменьшают скорость. Таким образом, работа может быть положительной и отрицательной в зависимости от направления силы и скорости.
Работа постоянной силы на криволинейном пути Пусть точка М движется по дуге окружности и сила F составляет некоторый угол α с касательной к окружности (рис. 15.5).
Вектор силы можно разложить на две составляющие:
Используя принцип независимости действия сил, определим работу каждой из составляющих силы отдельно:
Нормальная составляющая силы Fn всегда направлена перпендикулярно перемещению и, следовательно, работы не производит:
При перемещении по дуге обе составляющие силы разворачиваются вместе с точкой М. Таким образом, касательная составляющая силы всегда совпадает по направлению с перемещением. Будем иметь:
Касательную силу Ft обычно называют окружной силой. Работа при криволинейном пути — это работа окружной силы:
Произведение окружной силы на радиус называют вращающим моментом:
Работа силы, приложенной к вращающемуся телу, равна произведению вращающего момента на угол поворота:
Работа силы тяжести Работа силы тяжести зависит только от изменения высоты и равна произведению модуля силы тяжести на вертикальное перемещение точки (рис. 15.6):
где Δh — изменение высоты. При опускании работа положительна, при подъеме отрицательна.
Работа равнодействующей силы Под действием системы сил точка массой т перемещается из положения М1 в положение М2 (рис. 15.7). В случае движения под действием системы сил пользуются теоремой о работе равнодействующей. Работа равнодействующей на некотором перемещении равна алгебраической сумме работ системы сил на том же перемещении.
Примеры решения задач
Пример 1. Тело массой 200 кг поднимают по наклонной плоскости (рис. 15.8). Определите работу при перемещении на 10 м с постоянной скоростью. Коэффициент трения тела о плоскость f = 0,15. Решение
Решение 1. Работа силы тяжести зависит только от изменения высоты груза. Изменение высоты при перемещении из точки А в С:
2. Работа силы тяжести:
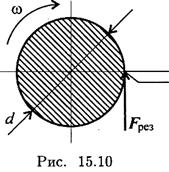
Пример 3. Определите работу силы резания за 3 мин. Скорость вращения детали 120 об/мин, диаметр обрабатываемой детали 40 мм, сила резания 1 кН (рис. 15.10). Решение
где Fpeз — сила резания. 2. Угловая частота вращения 120 об/мин. 3. Число оборотов за заданное время составляет z = 120 • 3 = 360 об. Угол поворота за это время
4. Работа за 3 мин Wp = 1 • 0,02 • 2261 = 45,2 кДж.
Пример 4. Тело массой m = 50 кг передвигают по полу при помощи горизонтальной силы Q на расстояние S = 6 м. Определить работу, которую совершит сила трения, если коэффициент трения между поверхностью тела и полом f = 0,3 (рис. 1.63). Решение
Согласно закону Аммонтона — Кулона сила трения
Сила трения направлена в сторону, противоположную движению, поэтому работа этой силы отрицательна:
Решение
Вращающий момент, передаваемый валом,
Выразим вращающий момент через усилия в ветвях ременной передачи:
откуда Тогда
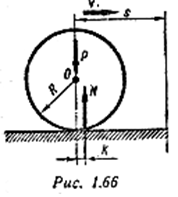
Пример 6. Колесо радиусом R = 0,3м катится без скольжения по горизонтальному рельсу (рис. 1.66). Найти работу трения качения при перемещении центра колеса на расстояние S = 30 м, если вертикальная нагрузка на ось колеса составляет Р = 100 кН. Коэффициент трения качения колеса по рельсу равен k = 0,005 см.
Трение качения возникает из-за деформаций колеса и рельса в зоне их контакта. Нормальная реакция N смещается вперед по направлению движения и образует с вертикальной силой давления Р на ось колеса пару, плечо которой равно коэффициенту трения качения k, а момент
Эта пара стремится повернуть колесо в направлении, противоположном его вращению. Поэтому работа трения качения будет отрицательной и определится как произведение постоянного момента трения на угол поворота колеса φ, т. е.
Путь, пройденный колесом, можно определить как произведение его угла поворота на радиус
откуда
Вводя значение φ в выражение работы и подставляя числовые значения, получаем
Контрольные вопросы и задания
1. Какие силы называют движущими? 2. Какие силы называют силами сопротивления? 3. Запишите формулы для определения работы при поступательном и вращательном движениях. 4. Какую силу называют окружной? Что такое вращающий момент? 5. Сформулируйте теорему о работе равнодействующей. ЛЕКЦИЯ 16
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 2505; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.008 с.) |


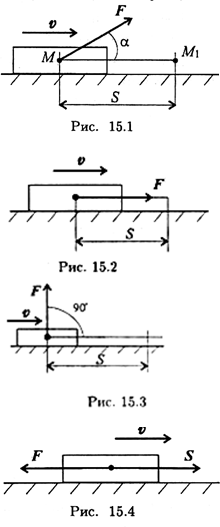 Работа силы в общем случае численно равна произведению модуля силы на длину пройденного пути и на косинус угла между направлением силы и направлением перемещения (рис. 15.1):
Работа силы в общем случае численно равна произведению модуля силы на длину пройденного пути и на косинус угла между направлением силы и направлением перемещения (рис. 15.1):
















 Пример 2. Определите работу силы тяжести при перемещении груза из точки А в точку С по наклонной плоскости (рис. 15.9). Сила тяжести тела 1500 Н. АВ = 6 м, ВС = 4 м.
Пример 2. Определите работу силы тяжести при перемещении груза из точки А в точку С по наклонной плоскости (рис. 15.9). Сила тяжести тела 1500 Н. АВ = 6 м, ВС = 4 м.


 1. Работа при вращательном движении
1. Работа при вращательном движении




 Пример 5. Определить натяжение ветвей ременной передачи (рис. 1.65), если мощность, передаваемая валом, N = 20 кВт, частота вращения вала п = 150 об/мин.
Пример 5. Определить натяжение ветвей ременной передачи (рис. 1.65), если мощность, передаваемая валом, N = 20 кВт, частота вращения вала п = 150 об/мин.



 Решение
Решение