
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение координат центра тяжести плоских фигурСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
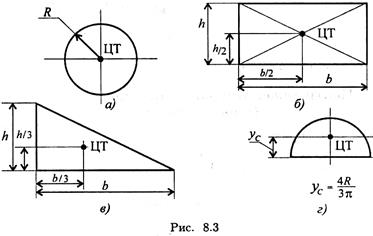
Положения центров тяжести простых геометрических фигур могут быть рассчитаны по известным формулам (рис. 8.3: а) — круг; б) — квадрат, прямоугольник; в) — треугольник; г) — полукруг).
Примечание. Центр тяжести симметричной фигуры находится на оси симметрии. Центр тяжести стержня находится на середине высоты. При решении задач используются следующие методы: 1. метод симметрии: центр тяжести симметричных фигур находится на оси симметрии; 2. метод разделения: сложные сечения разделяем на несколько простых частей, положение центров тяжести которых легко определить; 3. метод отрицательных площадей: полости (отверстия) рассматриваются как часть сечения с отрицательной площадью. Примеры решения задач Пример1. Определить положение центра тяжести фигуры, представленной на рис. 8.4. Решение
Аналогично определяется у С = 4,5 см.
Решение
Так как ферма симметричная, то ее центр тяжести лежит на оси симметрии DF. При выбранной (рис. 116) системе координатных осей абсцисса центра тяжести фермы
Неизвестной, следовательно, является лишь ордината уС центра тяжести фермы. Для ее определения разбиваем ферму на отдельные части (стержни). Длины их определяются из соответствующих треугольников. Из ΔAEF имеем
Из ΔADF имеем
Центр тяжести каждого стержня лежит в его середине, координаты этих центров легко определяются из чертежа (рис. 116). Найденные длины и ординаты центров тяжести отдельных частей фермы заносим в таблицу и по формуле
определяем ординату у с центра тяжести данной плоской фермы.
Следовательно, центр тяжести С всей фермы лежит на оси DF симметрии фермы на расстоянии 1,59 м от точки F.
Примечание. Часто рамы сваривают из разных профилей, создавая необходимую конструкцию. Таким образом, уменьшается расход металла и образуется конструкция высокой прочности. Для стандартных прокатных профилей собственные геометрические характеристики известны. Они приводятся в соответствующих стандартах.
Решение 1. Обозначим фигуры номерами и выпишем из таблиц необходимые данные: 1 — швеллер № 10 (ГОСТ 8240-89); высота h = 100 мм; ширина полки b = 46 мм; площадь сечения А1 = 10,9 см2; 2 — двутавр № 16 (ГОСТ 8239-89); высота 160 мм; ширина полки 81 мм; площадь сечения А2 — 20,2 см2; 3 — лист 5x100; толщина 5 мм; ширина 100мм; площадь сечения A3 = 0,5 • 10 = 5 см2.
2. Координаты центров тяжести каждой фигуры можно определить по чертежу. Составное сечение симметрично, поэтому центр тяжести находится на оси симметрии и координата х С = 0.
3. Определение центра тяжести составного сечения:
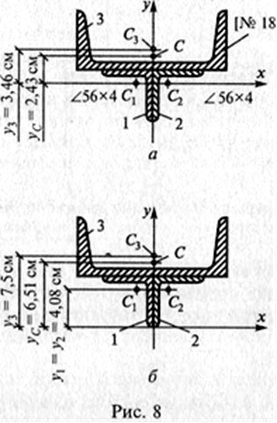
Пример 4. Определить координаты центра тяжести сечения, показанного на рис. 8, а. Сечение состоит из двух уголков 56x4 и швеллера № 18. Выполнить проверку правильности определения положения центра тяжести. Указать его положение на сечении.
Решение
1. Разобьем сечение на профили проката: два уголка 56 х 4 и швеллер № 18. Обозначим их 1, 2, 3 (см. рис. 8, а). 2. Укажем центры тяжести каждого профиля, используя табл. 1 и 4 прил. I, и обозначим их С1, С2, С3. 3. Выберем систему координатных осей. Ось у совместим с осью симметрии, а ось х проведем через центры тяжести уголков. 4. Определим координаты центра тяжести всего сечения. Так как ось у совпадает с осью симметрии, то она проходит через центр тяжести сечения, поэтому хс = 0. Координату ус определим по формуле
Пользуясь таблицами приложения, определим площади каждого профиля и координаты центров тяжести:
Координаты у1 и у2 равны нулю, так как ось х проходит через центры тяжести уголков. Подставим полученные значения в формулу для определения ус:
5. Укажем центр тяжести сечения на рис. 8, а и обозначим его буквой С. Покажем расстояние уС = 2,43 см от оси х до точки С. Поскольку уголки симметрично расположены, имеют одинаковую площадь и координаты, то А1 = А2, у1 = у2. Поэтому формула для определения уС может быть упрощена:
6. Выполним проверку. Для этого ось х проведем по нижнему краю полки уголка (рис. 8, б). Ось у оставим, как в первом решении. Формулы для определения хС и уС не изменяются:
Площади профилей останутся такими же, а координаты центров тяжестей уголков и швеллера изменятся. Выпишем их:
Находим координату центра тяжести:
По найденным координатам хс и ус наносим на рисунок точку С. Найденное двумя способами положение центра тяжести находится в одной и той же точке. Проверим это. Разница между координатами ус, найденными при первом и втором решении, составляет: 6,51 - 2,43 = 4,08 см. Это равно расстоянию между осями х при первом и втором решении: 5,6 - 1,52 = 4,08 см. Ответ: ус = 2,43 см, если ось х проходит через центры тяжести уголков, или ус = 6,51 см, если ось х проходит по нижнему краю полки уголка. Пример 5. Определить координаты центра тяжести сечения, изображенного на рис. 9, а. Сечение состоит из двутавра № 24 и швеллера №.24а. Показать положение центра тяжести на сечении.
Решение
1. Разобьем сечение на профили проката: двутавр и швеллер. Обозначим их цифрами 1 и 2. 3. Укажем центры тяжести каждого профиля С1 и С2, используя таблицы приложений. 4. Выберем систему осей координат. Ось х совместим с осью симметрии, а ось у проведем через центр тяжести двутавра. 5. Определим координаты центра тяжести сечения. Координата ус = 0, так как ось х совпадает с осью симметрии. Координату хс определим по формуле
По табл. 3 и 4 прил. I и схеме сечения определим
Подставим числовые значения в формулу и получим
5. Нанесем точку С (центр тяжести сечения) по найденным значениям хс и ус (см. рис. 9, а). Проверку решения необходимо выполнить самостоятельно при положении осей, как показано на рис. 9, б. В результате решения получим хс = 11,86 см. Разница между значениями хс при первом и втором решении равна 11,86 - 6,11 = 5,75 см, что равно расстоянию между осями у при тех же решениях bдв/2 = 5,75 см. Ответ: хс = 6,11 см, если ось у проходит через центр тяжести двутавра; хс = 11,86 см, если ось у проходит через левые крайние точки двутавра.
Пример 6. Железнодорожный кран опирается на рельсы, расстояние между которыми АВ = 1,5м (рис. 1.102). Сила тяжести тележки крана Gr = 30 кН, центр тяжести тележки находится в точке С, лежащей на линии KL пересечения плоскости симметрии тележки с плоскостью рисунка. Сила тяжести лебедки крана Qл = 10 кН приложена в точке D. Сила тяжести противовеса G„=20 кН приложена в точке Е. Сила тяжести стрелы Gc = 5 кН приложена в точке Н. Вылет крана относительно линии KL равен 2 м. Определить коэффициент устойчивости крана в ненагруженном состоянии и какой груз F можно поднять этим краном при условии, что коэффициент устойчивости должен быть не менее двух. Решение
1. В ненагруженном состоянии у крана возникает опасность опрокидывания при повороте вокруг рельса А. Следовательно, относительно точки А момент устойчивости
2. Опрокидывающий момент относительно точки А создается силой тяжести противовеса, т. е.
3. Отсюда коэффициент устойчивости крана в ненагруженном состоянии
4. При нагрузке стрелы крана грузом F возникает опасность опрокидывания крана с поворотом около рельса В. Следовательно, относительно точки В момент устойчивости
5. Опрокидывающий момент относительно рельса В
6. По условию задачи эксплуатация крана разрешается при коэффициенте устойчивости kB ≥ 2, т. е.
Отсюда
Контрольные вопросы и задания
1. Почему силы притяжения к Земле, действующие на точки тела, можно принять за систему параллельных сил?
2. Запишите формулы для определения положения центра тяжести неоднородных и однородных тел, формулы для определения положения центра тяжести плоских сечений.
3. Повторите формулы для определения положения центра тяжести простых геометрических фигур: прямоугольника, треугольника, трапеции и половины круга. 4. 5. Вычислите статический момент данной фигуры относительно оси Ox. h = 30 см; b = 120 см; с = 10 см (рис. 8.6).
6. Определите координаты центра тяжести заштрихованной фигуры (рис. 8.7). Размеры даны в мм.
7. Определите координату у фигуры 1 составного сечения (рис. 8.8). При решении воспользоваться справочными данными таблиц ГОСТ «Сталь горячекатанная» (см. Приложение 1).
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 21171; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.10.101 (0.009 с.) |

 Разбиваем фигуру на три части:
Разбиваем фигуру на три части: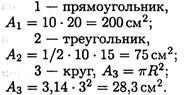

 Пример 2. Найти положение центра тяжести симметричной стержневой фермы ADBE (рис. 116), размеры которой таковы: АВ = 6м, DE = 3 м и EF = 1 м.
Пример 2. Найти положение центра тяжести симметричной стержневой фермы ADBE (рис. 116), размеры которой таковы: АВ = 6м, DE = 3 м и EF = 1 м.







 Пример 3. Определить координаты центра тяжести составного сечения. Сечение состоит из листа и прокатных профилей (рис. 8.5).
Пример 3. Определить координаты центра тяжести составного сечения. Сечение состоит из листа и прокатных профилей (рис. 8.5).

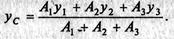












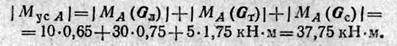






 Что называют статическим моментом площади?
Что называют статическим моментом площади?


