
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Центр параллельных сил. Центр тяжестиСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Найдем координаты т. С (рис. 25) c помощью теоремы Вариньона. Поскольку mx ( Отсюда находим: где yk - координата y точки приложения силы Fk. Аналогично определяем координату xС: Тогда Для определения z Отсюда находим: Силы тяжести, действующие на тело, можно приближенно считать системой параллельных сил. Центр системы сил тяжести называется центром тяжести. Определение: центром тяжести называется точка, через которую проходит равнодействующая сил тяжести точек тела при повороте тела на любой угол. Для определения координат центра тяжести тела можно использовать формулы, полученные ранее для координат центра параллельных сил. Если тело неоднородно, то, разбивая его на несколько простых тел (конечных элементов), для которых легко определяются координаты центра тяжести, получаем формулы для определения координат центра тяжести неоднородного тела:
где Pk - сила тяжести элемента тела с номером k. Если тело однородное, то: где V k - объем элемента с номером k; Если у тела два размера много больше третьего, то говорят о центре тяжести поверхности, в этом случае: Где Sk - площадь элемента поверхности тела с номером k; h – толщина поверхности. Если h = const, то подставив (4) в (2), получим аналогичные формулы, в которых вместо P будет стоять S. Если у тела один размер много больше двух других, то говорят о центре тяжести линии. В этом случае, если площадь сечения S постоянна,
где L k - длина элемента линии с номером k. Подставляя (5) в (2), получим формулы, аналогичные (2), в которых вместо P будет находиться L. Аналитические и экспериментальные методы определения положения центра тяжести К аналитическим методам определения положения центра тяжести относятся метод разбиений и метод отрицательных площадей.
2. Метод отрицательных площадей. Заключается в том, что данное тело дополняют до простейшего. При этом дополняющие элементы (их вес, объем, площадь или длину) считают отрицательными. Простейшими являются тела, у которых известно положение центра тяжести (ЦТ). Это: однородные диск и окружность, их ЦТ. находится в центре; прямоугольник и параллелограмм, их ЦТ находится в точке пересечения диагоналей; треугольник, его ЦТ находится в точке пересечения медиан. При этом следует учитывать, что медианы точкой их пересечения делятся в отношении 1:2 (рис. 26). Положение центра тяжести кругового сектора можно определить по формуле: ОС=2/3∙R∙ sinα/α, где α – половина центрального угла, выраженного врадианах (рис. 27). ЦТ тела, имеющего центр, плоскость или ось симметрии находится на них. Из экспериментальных способов отметим методы взвешивания и подвешивания.
х = R∙a /P. Метод подвешивания ( применяется преимущественно для плоских тел). При этом способе тело подвешивают на нити сначала в одной точке и проводят линию, продолжающую нить, затем в другой точке. Точка пересечения этих линий определит положение ЦТ. Трение скольжения
Коэффициент трения не зависит от площади соприкасающихся поверхностей, незначительно зависит от скорости. Коэффициент трения покоя больше коэффициента трения при движении и несколько уменьшается с увеличением скорости.
Реакция шероховатой поверхности R (рис. 29) есть сумма векторов нормальной реакции N и касательной реакции, т.е. силы трения. Реакция R отклонена от нормали. Максимальный угол отклонения реакции шероховатой поверхности от нормали φ называется углом трения. Его можно найти по формуле: tg φ = Fтр/N = f. Если равнодействующая F внешних сил, приложенных к телу, проходит внутри угла трения, то тело не выйдет из равновесия при сколь угодно значительном модуле силы Трение качения В теоретической механике все тела считаются абсолютно твердыми. В этом идеальном случае тело (рис. 30) вышло бы из состояния покоя при сколь угодно малой силе F, т.к. сумма моментов сил, приложенных к телу, не равна 0, однако этого не происходит. В действительности все тела деформируемы, поэтому нормальная реакция N (рис. 31) смещается в направлении действия силы F, образуя вместе с силой тяжести пару сил, препятствующую качению. Максимальное F ∙ R Здесь R – радиус цилиндра. Условие, при котором начинается скольжение: F Поскольку f >> δ/R, то при скольжении надо приложить силу во много раз большую, чем при качении. Задача С1 Жесткая рама (рис. С1.0-С.1.9, табл. С1) находится под действием пары сил с моментом М = 20 кН×м и двух сосредоточенных сил, значения которых указаны в таблице. В точке С к раме прикреплен трос, перекинутый через блок и несущий на конце груз весом Р=25 кН. Определить реакции связей, вызываемые действующими нагрузками. При окончательных расчетах принять a= 0,5 м. Указания. Задача С1 – на равновесие тела под действием произвольной плоской системы сил. Данные для решения задачи взять из таблицы С1. При вычислении момента силы F часто удобно разложить ее на составляющие F’ и F’’, для которых плечи легко определяются, и воспользоваться теоремой Вариньона, тогда Таблица С1
Пример C1
Дано: F = 25 кН, α = 60˚, Р = 18 кН, γ = 75˚, М = 50 кН×м, β = 30˚, α = 0,5 м. Определить: реакции в точках А и В, вызываемые действующими нагрузками. 1.Рассмотрим равновесие рамы. Введем координатные оси xy и изобразим действующие на раму силы: силу
2. Для полученной плоской системы сил составим три уравнения равновесия (основная форма). При вычислении момента силы
Подставив в составленные уравнения числовые значения заданных величин и решив эти уравнения, определим искомые реакции. Ответ: x А=-8,5 кН; y А=-23,3 кН; RB=7,3 кН. Знаки указывают, что силы Задача С2 Конструкция состоит из жесткого угольника и стержня, которые в точке С или соединены друг с другом шарнирно (рис. С2.0 – С2.5), или свободно опираются друг о друга (рис. С2.6-С2.9). На каждую конструкцию действуют: пара сил с моментом М=60 кН×м, равномерно распределенная нагрузка интенсивности q = 20 кН/м и еще две силы. Эти силы, направления и точки их приложения указаны в табл. С2; там же в столбце «Участок» указано, на каком участке действует распределенная нагрузка. Определить реакции связей в точках А, В, С и D, вызванные заданными нагрузками. При окончательных расчетах принять а = 0,2 м. Направление распределенной нагрузки на различных по расположению участках указано в табл. С2а. Указания. Задача С2 на равновесие системы тел, находящихся под действием плоской системы сил. При ее решении можно рассмотреть сначала равновесие всей системы в целом, а затем – равновесие одного из тел системы, изобразив его отдельно, или же сразу расчленить систему и рассмотреть равновесие каждого из тел в отдельности, учтя при этом закон равенства действия и противодействия. Таблица С2
Таблица С2а
Пример C2. На угольник ABC (<ABC=90˚), конец А которого жестко заделан, в точке С опирается стержень DE (рис. С2 а).
Стержень имеет в точке D неподвижную шарнирную опору, и к нему приложена сила Дано: F=10 кН, М =5 кН×м, q =20 кН/м, а = 0,2 м. Определить: реакции в точках А, С, D, вызванные заданными нагрузками. Решение. 1. Для определения реакции расчленим систему и рассмотрим сначала равновесие стержня DE (рис. С2 б). Проведем координатные оси xy и изобразим действующие на стержень силы: силу
2. Теперь рассмотрим равновесие угольника (рис. С2 в). На него действуют сила давления стержня
При вычислении момента силы разлагаем ее на составляющие искомые реакции. При решении учитываем, что численно N′=N в силу равенства действия и противодействия. Ответ: N= 21,7 кН, YD=-10,8 кН; ХD=8,8 кН,ХА=-26,8 кН, УА = 24,7 кН, МА = - 42,6 кН×м. Знаки указывают, что силы Задача С3 Ферма, состоящая из 7 стержней и пяти узлов, закреплена, как показано на рис. С3.0 - С3.9. В узлах фермы приложены две сосредоточенные силы, значения которых и точки их приложения указаны в таблице С3. Здесь же даны размеры фермы. Требуется методом вырезания узлов определить усилия во всех стержнях фермы. Для трех стержней фермы (по усмотрению студента) сделать проверку методом сечений. Указание. Вначале необходимо составить уравнения равновесия для всей фермы в целом и определить три неизвестные реакции опор. Таблица С3
В узлах фермы С и D (рис. С3) приложены силы: F1 =10 H, и F2 =20 H. Определить усилия во всех стержнях фермы методом вырезания узлов. Кроме того, определить усилия в стержнях 2, 3, 4 методом сечений. Размеры указаны на рисунке.
1. Определим реакции опор: xA, yA, RB. Для этого составим уравнения равновесия для всей фермы в целом.
Решая уравнения (С3.1) – (С3.2), находим: xA = - 16,309 Н; yA = 1,752 Н; RB = 15,297 Н.
Далее можно рассмотреть равновесие узла В (в нем сходится два стержня) или узла С (рис. С3б). В узле С сходится три стержня, но усилие s 1 нами уже определено, поэтому из уравнений равновесия можно найти s 2, s 3. Угол α определим из треугольника АЕС: Составим уравнения равновесия:
Решая эту систему уравнений, находим: s 3 = 11,254 H, s 2 = -17,663 H. Отрицательные значения усилий в первом и втором стержнях показывают, что эти стержни не растянуты, как предполагалось, а сжаты. Далее можно рассмотреть равновесие узла Е и определить s 5, s 6. Из уравнения проекций на ось у для узла D можно найти усилие в седьмом стержне s 7. Уравнения равновесия для узла В должны обратиться в тождество, они являются уравнениями проверки. 3. Определим усилия в стержнях 2, 3, 4 методом сечений. Рассечем ферму сечением I-I (рис. С3в) и составим уравнения равновесия для части фермы, расположенной слева от сечения.
Из уравнения (С.3.4) находим s2 = -17,663 H. Из уравнения (С.3.5) находим s3 = 11,254 H. Из уравнения (С.3.6) находим s4 = 16,309 H. Сравнивая эти результаты с полученными ранее, делаем вывод, что задача решена правильно. Задача С4 Шесть невесомых стержней соединены концами шарнирно друг с другом в двух узлах и прикреплены другими концами (тоже шарнирно) к неподвижным опорам А, В, С, D (рис. С4.0-С4.9, табл. С4). Стержни и узлы (узлы расположены в вершинах Н, К, L или М прямоугольного параллелепипеда) на рисунках не показаны и должны быть изображены решающим задачу по данным таблицы. В узле, который в каждом столбце таблицы указан первым, приложена сила Р=200 Н; во втором узле приложена сила Q=100 H. Сила Указания. Задача С4 – на равновесие пространственной системы сходящихся сил. При ее решении следует рассмотреть отдельно равновесие каждого из двух узлов. Таблица С4
Пример С4.
Дано: Р = 100 Н, a1 = 60°, b1 = 60°, g1 = 45°, Q = 50 H, a2 = 45°, b2 = 60°, g2 = 60°; y = 30°, j = 60°, d ≈ 74°. Определить: усилия в стержнях 1- 6. Решение 1. Рассмотрим равновесие узла К, в котором сходятся стержни 1, 2, 3. на узел действуют сила
Решив уравнения (С4.1) - (С4.3) при заданных числовых значениях силы Р и углов, получим: N1 = 349 H, N2 = - 345 H, N3 = 141 H. 2. Рассмотрим равновесие узла М. На него действует силы Составим уравнения равновесия:
При определении проекций силы (по величине Ответ:N1 = 349 H; N2 = - 345 H; N3=141 H; N4 = 50 H; N5 = 329 H; N6 = - 66 H. Знаки показывают, что стержни 2 и 6 сжаты; остальные – растянуты. Задача С5 Две однородные прямоугольные тонкие плиты жестко соединены (сварены) под прямым углом друг к другу и закреплены, как показано на рис. С5.0-С5.9. Размеры плит указаны на рисунках; вес большей плиты Р1 = 5 кН, вес меньшей плиты Р2 = 3 кН. каждая из плит расположена параллельно одной из координатных плоскостей (плоскость xy горизонтальная). На плиты действует пара сил с моментом М = 4 кН×м, лежащая в плоскости одной из плит, и две силы. Значения этих сил, их направления и точки приложения указаны в табл. С5; при этом силы
Указания. Задача С5 – на равновесие тела под действием произвольной пространственной системы сил. При ее решении учесть, что реакция сферического шарнира (подпятника) имеет три составляющие (по всем трем координатным осям), а реакция цилиндрического шарнира (подшипника) – две составляющие, лежащие в плоскости, перпендикулярной оси шарнира (подшипника). При вычислении момента силы
Таблица С5
Горизонтальная прямоугольная плита весом Р (рис. С5) закреплена сферическим шарниром
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 567; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.110.45 (0.016 с.) |

 Центром параллельных сил называется точка С, через которую проходит равнодействующая системы параллельных сил, при любом повороте всех сил системы в одном и том же направлении на один и тот же угол.
Центром параллельных сил называется точка С, через которую проходит равнодействующая системы параллельных сил, при любом повороте всех сил системы в одном и том же направлении на один и тот же угол. ) =
) =  , то
, то  .
.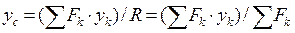 ,
, , или
, или  .
. .
. повернем все силы системы так, чтобы они стали параллельны оси y, тогда
повернем все силы системы так, чтобы они стали параллельны оси y, тогда  , или
, или  .
. .
. (2)
(2) , (3)
, (3) - удельный вес. В этом случае говорят о центре тяжести объема. Подставив (3) в (2) и сократив на
- удельный вес. В этом случае говорят о центре тяжести объема. Подставив (3) в (2) и сократив на 
 , (4)
, (4)
 , (5)
, (5) 1. Метод разбиений. Метод заключается в мысленном разбиении тела на несколько простейших (конечных элементов), для которых известно положение центра тяжести. Используют формулы вида (2).
1. Метод разбиений. Метод заключается в мысленном разбиении тела на несколько простейших (конечных элементов), для которых известно положение центра тяжести. Используют формулы вида (2). Метод взвешивания (рис. 28). По известным весу тела P, показаниям весов R и расстоянию a определяют расстояние х из уравнения: ∑mO = - P∙x + R∙a; откуда
Метод взвешивания (рис. 28). По известным весу тела P, показаниям весов R и расстоянию a определяют расстояние х из уравнения: ∑mO = - P∙x + R∙a; откуда При попытке сдвинуть одно тело относительно другого возникает сила, препятствующая этому. Она называется силой трения. Гладкая поверхность – это идеализированная поверхность (без трения). Реальные поверхности обладают шероховатостью. Силу трения находят из уравнений равновесия. В предельном случае, предшествующем срыву, т.е. выходу из состояния покоя, силу трения можно определить по формуле: Fтр = N∙f, где N – сила нормального давления; f – коэффициент трения покоя (безразмерная величина, определяемая экспериментально).
При попытке сдвинуть одно тело относительно другого возникает сила, препятствующая этому. Она называется силой трения. Гладкая поверхность – это идеализированная поверхность (без трения). Реальные поверхности обладают шероховатостью. Силу трения находят из уравнений равновесия. В предельном случае, предшествующем срыву, т.е. выходу из состояния покоя, силу трения можно определить по формуле: Fтр = N∙f, где N – сила нормального давления; f – коэффициент трения покоя (безразмерная величина, определяемая экспериментально). .
. (предельное) смещение δ называется коэффициентом трения качения ( измеряется в см или мм). В задачах теоретической механики, когда сопротивление качению необходимо учесть, цилиндрические тела считают абсолютно твердыми и к ним прикладывают момент M
(предельное) смещение δ называется коэффициентом трения качения ( измеряется в см или мм). В задачах теоретической механики, когда сопротивление качению необходимо учесть, цилиндрические тела считают абсолютно твердыми и к ним прикладывают момент M  N ∙ δ или F
N ∙ δ или F 
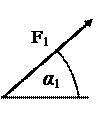



















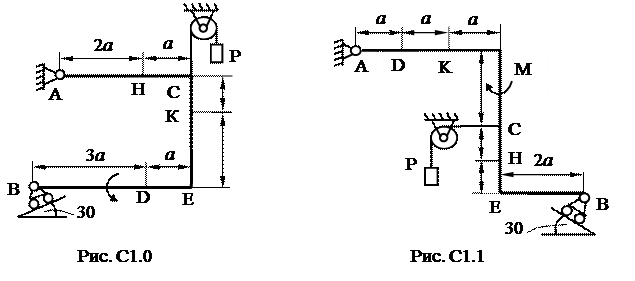

















 Изогнутый стержень (рама BCDА, рис. С1) имеет в точке А неподвижную шарнирную опору, а в точке В – подвижную шарнирную опору на катках. Все действующие нагрузки и размеры показаны на рисунке.
Изогнутый стержень (рама BCDА, рис. С1) имеет в точке А неподвижную шарнирную опору, а в точке В – подвижную шарнирную опору на катках. Все действующие нагрузки и размеры показаны на рисунке. , пару сил с моментом М, натяжение троса
, пару сил с моментом М, натяжение троса  (по модулю Т=Р) и реакции связей
(по модулю Т=Р) и реакции связей  (реакцию неподвижной шарнирной опоры А изображаем двумя ее составляющими, реакцию подвижного шарнира направим перпендикулярно опорной плоскости).
(реакцию неподвижной шарнирной опоры А изображаем двумя ее составляющими, реакцию подвижного шарнира направим перпендикулярно опорной плоскости). на составляющие
на составляющие  и учтем, что
и учтем, что  Получим:
Получим: (С1.1)
(С1.1)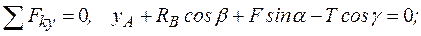 (С1.2)
(С1.2) (С1.2)
(С1.2) и
и  направлены противоположно показанным на рис. С1.
направлены противоположно показанным на рис. С1.

























 , реакцию
, реакцию  , направленную перпендикулярно стержню, и составляющие
, направленную перпендикулярно стержню, и составляющие 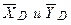 реакции шарнира D. Для полученной плоской системы сил составляем три уравнения равновесия:
реакции шарнира D. Для полученной плоской системы сил составляем три уравнения равновесия: (С2.1)
(С2.1) (С2.2)
(С2.2) (С2.3)
(С2.3) , направленная противоположно реакции
, направленная противоположно реакции  , приложенной в середине участка КВ (численно Q = q×4a = 16 кН), пара сил с моментом М и реакция жесткой заделки, слагающаяся из силы, которую представим составляющими
, приложенной в середине участка КВ (численно Q = q×4a = 16 кН), пара сил с моментом М и реакция жесткой заделки, слагающаяся из силы, которую представим составляющими 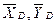 , и пары с моментом МА. Для этой плоской системы сил тоже составляем три уравнения равновесия:
, и пары с моментом МА. Для этой плоской системы сил тоже составляем три уравнения равновесия: (С2.3)
(С2.3) (С2.4)
(С2.4) (С2.5)
(С2.5) и
и  и применяем теорему Вариньона. Подставив в составленные уравнения числовые значения заданных величин и решив систему уравнений (С2.1) – (С2.6), найдем
и применяем теорему Вариньона. Подставив в составленные уравнения числовые значения заданных величин и решив систему уравнений (С2.1) – (С2.6), найдем и момент МА направлены противоположно показанным на рисунках.
и момент МА направлены противоположно показанным на рисунках.














 Пример С3.
Пример С3. (С3.1)
(С3.1) (С3.2)
(С3.2) (С3.3)
(С3.3) 2. Определим усилия в стержнях фермы методом вырезания узлов. Вначале будем полагать, что все стержни растянуты, тогда их реакции будут направлены вовнутрь стержней. Покажем все силы, действующие на узел А (рис. С3а). Поскольку в узле А сходится только 2 стержня, то усилия в этих стержнях можно определить из уравнений равновесия:
2. Определим усилия в стержнях фермы методом вырезания узлов. Вначале будем полагать, что все стержни растянуты, тогда их реакции будут направлены вовнутрь стержней. Покажем все силы, действующие на узел А (рис. С3а). Поскольку в узле А сходится только 2 стержня, то усилия в этих стержнях можно определить из уравнений равновесия:
 Отсюда
Отсюда 
 Тогда
Тогда 
 , тогда α = 36,9º, и sin α = 0,6; cos α = 0,8.
, тогда α = 36,9º, и sin α = 0,6; cos α = 0,8.


 (3.4)
(3.4) (3.5)
(3.5) (3.6)
(3.6) образует с положительными направлениями координатных осей х, y, z заданные углы, равные соответственно a1 = 45°, b1 = 60°, g1 = 60°, а сила Q – углы a2 = 60°, b2 = 45°, g2 = 60. Грани параллелепипеда, параллельные плоскости xy, - квадраты. Диагонали других (боковых) граней образуют с плоскостью xy угол j = 60°, а диагональ параллелепипеда образует с этой плоскостью угол q = 51°. Определить усилия в стержнях полученной пространственной фермы.
образует с положительными направлениями координатных осей х, y, z заданные углы, равные соответственно a1 = 45°, b1 = 60°, g1 = 60°, а сила Q – углы a2 = 60°, b2 = 45°, g2 = 60. Грани параллелепипеда, параллельные плоскости xy, - квадраты. Диагонали других (боковых) граней образуют с плоскостью xy угол j = 60°, а диагональ параллелепипеда образует с этой плоскостью угол q = 51°. Определить усилия в стержнях полученной пространственной фермы.




 Конструкция (пространственная ферма) состоит из невесомых стержней 1, 2, …,6, соединенных друг с другом (в узлах К и М) и с неподвижными опорами А, В, С, D шарнирами (рис. С4). В узлах К и М приложены силы
Конструкция (пространственная ферма) состоит из невесомых стержней 1, 2, …,6, соединенных друг с другом (в узлах К и М) и с неподвижными опорами А, В, С, D шарнирами (рис. С4). В узлах К и М приложены силы  и
и  , образующие с координатными осями углы a1, b1, g1 и a2, b2, g2 соответственно (на рисунке показаны только углы a1, b1, g1).
, образующие с координатными осями углы a1, b1, g1 и a2, b2, g2 соответственно (на рисунке показаны только углы a1, b1, g1). и реакции
и реакции  стержней, которые направим по стержням от узла, считая стрежни растянутыми. Составим уравнения равновесия этой пространственной системы сходящихся сил:
стержней, которые направим по стержням от узла, считая стрежни растянутыми. Составим уравнения равновесия этой пространственной системы сходящихся сил:

 (С4.1)
(С4.1) (С4.2)
(С4.2) (С4.3)
(С4.3) ,
,  . При этом по закону о равенстве действия и противодействия реакция
. При этом по закону о равенстве действия и противодействия реакция  направлена противоположно
направлена противоположно  , численно же N′2 = N2.
, численно же N′2 = N2. (С4.4)
(С4.4) (С4.5)
(С4.5) (С4.6)
(С4.6) на оси х и у в уравнениях (С4.4) и (С4.5) удобно сначала найти проекцию
на оси х и у в уравнениях (С4.4) и (С4.5) удобно сначала найти проекцию  этой силы на плоскость xOy
этой силы на плоскость xOy ), а затем найденную проекцию на плоскость спроецировать на оси. Решив систему уравнений (С4.4) - (С4.6) и учитывая,что:
), а затем найденную проекцию на плоскость спроецировать на оси. Решив систему уравнений (С4.4) - (С4.6) и учитывая,что: 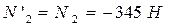 , найдем силы N4, N5, N6.
, найдем силы N4, N5, N6. и
и  лежат в плоскостях, параллельных плоскости xy, сила
лежат в плоскостях, параллельных плоскости xy, сила  ─ в плоскости, параллельной xz, и сила
─ в плоскости, параллельной xz, и сила  в плоскости, параллельной yz. Точки приложения сил (D, E, H, K) находятся в углах или в серединах сторон плит. Определить реакции связей в точках А и В и реакцию стержня (стержней). Принять a = 0,6 м.
в плоскости, параллельной yz. Точки приложения сил (D, E, H, K) находятся в углах или в серединах сторон плит. Определить реакции связей в точках А и В и реакцию стержня (стержней). Принять a = 0,6 м. , параллельные координатным осям, (или на три); тогда по теореме Вариньона, записанной относительно оси ох,
, параллельные координатным осям, (или на три); тогда по теореме Вариньона, записанной относительно оси ох,  .
.













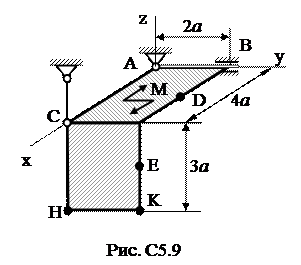
 Пример С5
Пример С5


