
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение движения центра масс.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Основной закон динамики
Это есть уравнение движения центра масс системы, одно из важнейших уравнений механики. Оно утверждает, что центр масс любой системы частиц движется так, как если бы вся масса системы была сосредоточена в этой точке и к ней были бы приложены все внешние силы. Ускорение центра масс системы совершенно не зависит от точек приложения внешних сил. Если Пример: однородный цилиндр массы

Совместное решение дает значение параметров Уравнение движения центра масс Систему отсчета, жестко связанную с центром масс, которая движется поступательно относительно ИСО называют системой центра масс. Ее особенностью является то, что полный импульс системы частиц в ней всегда равен нулю, так, как
Работа и энергия Работа
Действие силы на перемещении
 Значит, элементарная работа Значит, элементарная работа  (*) (*)
Суммируя элементарные работы (т.е., интегрируя) по всем элементарным участкам пути от 1 к 2 найдем работу силы
Геометрический смысл этого выражения виден из рисунка, на котором Размерность работы Найдем для примера работу некоторых центральных сил. 1. Работа гравитационной или кулоновской силы.
Пусть в точке О находится неподвижная материальная точка, действующая на частицу М с силой Тогда 2. Работа упругой силы
3. Работа силы тяжести Работа всех рассмотренных сил не зависит от формы пути между точками 1 и 2, а зависит только от положения этих точек. Эта особенность присуща не всем силам. Силы трения, например, не обладают таким свойством.
4.2 Мощность по определению это работа, выполненная за единицу времени. Если за промежуток времени
Зная Единица мощности в системе СИ
Консервативные силы Если в каждой точке пространства на частицу, помещенную туда, действует сила, говорят, что частица находится в поле сил, например в поле сил тяжести, гравитационной, кулоновской и других сил. Поле сил может быть постоянным во времени, тогда оно называется стационарным. Стационарное поле в одной системе отсчета, может быть нестационарным в другой. В стационарном поле сила, действующая на частицу, зависит только от её положения в пространстве.
Разобъем произвольный замкнутый контур на две части: 1а2 и 2в1, рис. Тогда работа на всем пути:
 , поскольку , поскольку  , то , то  . А так как работа не зависит от пути, то . А так как работа не зависит от пути, то  и, значит, и, значит,  . .
К неконсервативным силам относятся силы трения и сопротивления. Работа этих сил зависит от пути между начальным и конечным положением частицы и не равна нулю на замкнутом пути. Центральные силы.
Если силы зависят только от расстояния между взаимодействующими частицами и направлены вдоль прямой их соединяющей, то они называются центральными. Их примером являются гравитационные, кулоновские и упругие силы. Центральные силы можно записать как
Докажем, что центральные силы являются консервативными. Найдем сначала работу центральной силы в случае, когда силовое поле создано одной неподвижной частицей О. Элементарная работа над частицей М равна:
Если на частицу в силовом поле действует несколько центральных сил, то работа при перемещении из т.1 в т. 2 равна алгебраической сумме работ отдельных сил Таким образом, центральные силы являются консервативными.
|
||||||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 2363; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.122.95 (0.01 с.) |

 можно записать в иной форме, зная понятие центра масс системы:
можно записать в иной форме, зная понятие центра масс системы:
 , то
, то 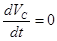 , значит
, значит  и
и  — это случай замкнутой системы в инерциальной системе отсчета. Таким образом, если центр масс системы движется равномерно и прямолинейно, это означает, что её импульс сохраняется в процессе движения.
— это случай замкнутой системы в инерциальной системе отсчета. Таким образом, если центр масс системы движется равномерно и прямолинейно, это означает, что её импульс сохраняется в процессе движения. и радиуса
и радиуса  скатывается без скольжения по наклонной плоскости, составляющей угол
скатывается без скольжения по наклонной плоскости, составляющей угол  с горизонтом. Найти уравнение движения?
с горизонтом. Найти уравнение движения?




 совпадает с основным уравнением динамики материальной точки и является его обобщением на систему частиц: ускорение системы как целого пропорционально результирующей всех внешних сил и обратно пропорционально массе системы.
совпадает с основным уравнением динамики материальной точки и является его обобщением на систему частиц: ускорение системы как целого пропорционально результирующей всех внешних сил и обратно пропорционально массе системы. .
. Пусть частица М под действием силы
Пусть частица М под действием силы  совершает перемещение по некоторой траектории 1-2. Сила, в общем случае, может меняться во времени по модулю и направлению, но на элементарном перемещении
совершает перемещение по некоторой траектории 1-2. Сила, в общем случае, может меняться во времени по модулю и направлению, но на элементарном перемещении  её можно считать
её можно считать  .
. , которая называется элементарной работой силы
, которая называется элементарной работой силы  на перемещении
на перемещении  , где
, где  - элементарный путь
- элементарный путь  проекция вектора
проекция вектора 
 - величина алгебраическая, она может быть
- величина алгебраическая, она может быть  , или
, или  , а также равна нулю при
, а также равна нулю при  .
. .
. и высотой
и высотой  ;
; 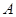 - площадь под всей кривой. Над осью работа силы положительна, под осью — отрицательна.
- площадь под всей кривой. Над осью работа силы положительна, под осью — отрицательна. .
.


 ;
;  —орт радиуса- вектора
—орт радиуса- вектора  , a -постоянная, равная -jm1m2 для гравитационной и kq1q2 для кулоновской силы. Элементарная работа этой силы на перемещении
, a -постоянная, равная -jm1m2 для гравитационной и kq1q2 для кулоновской силы. Элементарная работа этой силы на перемещении  ; Скалярное произведение
; Скалярное произведение  — приращение модуля вектора
— приращение модуля вектора 
 , а работа на всем пути:
, а работа на всем пути:  .
.
 ;Здесь
;Здесь  -проекция вектора
-проекция вектора  .
. Элементарная работа силы тяжести:
Элементарная работа силы тяжести:  ; Скалярное произведение
; Скалярное произведение  — приращение координаты
— приращение координаты  . Тогда
. Тогда ; А работа на пути 1-2 равна
; А работа на пути 1-2 равна  .
. сила
сила  , то мощность, развиваемая этой силой в данный момент времени
, то мощность, развиваемая этой силой в данный момент времени  т.е. скалярное произведение
т.е. скалярное произведение  , с которой движется точка приложения данной силы:
, с которой движется точка приложения данной силы:  .
. — как и работа, величина алгебраическая.
— как и работа, величина алгебраическая. :
:  , поскольку
, поскольку  , то
, то  , тогда:
, тогда: 
 .
. Работа, которую совершают силы поля по перемещению частицы из т.1 в т.2 зависит, в общем случае, от формы пути между этими точками, например, при перемещении с участием сил трения. Однако, имеются стационарные силовые поля, в которых работа сил поля над частицей не зависит от пути между т.1 и т.2. Силы, обладающие таким свойством называются консевативными. Это свойство можно сформулировать другим способом: силы поля являются консервативными, если их работа в стационарном поле на любом замкнутом пути равна нулю.
Работа, которую совершают силы поля по перемещению частицы из т.1 в т.2 зависит, в общем случае, от формы пути между этими точками, например, при перемещении с участием сил трения. Однако, имеются стационарные силовые поля, в которых работа сил поля над частицей не зависит от пути между т.1 и т.2. Силы, обладающие таким свойством называются консевативными. Это свойство можно сформулировать другим способом: силы поля являются консервативными, если их работа в стационарном поле на любом замкнутом пути равна нулю. Всякое силовое поле вызвано действием определенного тела или системы тел. Сила, действующая на частицу в этом поле обусловлена взаимодействием этой частицы с телами.
Всякое силовое поле вызвано действием определенного тела или системы тел. Сила, действующая на частицу в этом поле обусловлена взаимодействием этой частицы с телами. , здесь
, здесь  является функцией только расстояния
является функцией только расстояния  относительно частицы О.
относительно частицы О. ; поскольку
; поскольку  - проекция вектора перемещения на вектор
- проекция вектора перемещения на вектор  . Этот интеграл не зависит от формы пути, а зависит только от вида функции
. Этот интеграл не зависит от формы пути, а зависит только от вида функции  и
и  т.е. от расстояний.
т.е. от расстояний. , а, т.к., работа каждой из них не зависит от пути, то и работа результирующей силы также от пути не зависит.
, а, т.к., работа каждой из них не зависит от пути, то и работа результирующей силы также от пути не зависит.


