
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Концентрации электронов и дырокСодержание книги Поиск на нашем сайте
Дополнительные главы физики Вопросы к экзамену
1. Собственные полупроводники. Концентрация электронов и дырок в собственном полупроводнике. Понятие «эффективная масса» Собственные полупроводники -это полупроводники, в которых нет примесей Концентрации электронов и дырок
В отсутствии внешних воздействий (освещение, электро-магнитное поле) будем обозначать концентрацию свободных электронов и дырок с инексом 0 ( Где
Эффективная масса Для того чтобы использовать для описания движения электронов и дырок в полупроводниках в классическом представлении вводят понятие эффективных масс электронов и дырок (
Будут справедливы если вместо массы свободного электрона (электрона в вакууме)
Эффективная масса учитывает влияние периодического потенциала атома в кристалле проводника на движение электронов и дырок и определяется уравнением дисперсии
Примесные полупроводники. Концентрация электронов и дырок в примесном полупроводнике. Понятие «легирование»
Примесный полупроводник - это полупроводник с примесями. Процесс введения примесей в полупроводник называется легированием полупроводника, а сами примеси называют легирующими Концентрация электронов и дырок
Данное уравнение справедливо только для равновесных носителей заряда, т.е. в отсутствии внешних воздействий.
2. Уровень Ферми и определение его положения
Энергия Ферми- это максимальная энергия электронов при
Энергия Ферми растет с увеличением количества электронов в квантовой системе и, соответственно, уменьшается с их уменьшением.
В любом п/п при стремлении температуры к абсолютному нулю уровень Ферми находится посередине запрещенной зоны, но при повышении температуры в примесном п/п он смещается либо вверх либо вниз. Причина этого в переходе электронов из валентной зоны в зону проводимости или наоборот, что обуславливает изменение энергии зоны проводимости и последующее смещение уровня Ферми. В случае с беспримесными полупроводниками, уровень Ферми при любой температуре проходит по середине запрещенной зоны.
В случае с p--полупроводниками, наблюдается обратная ситуация: чем большая концентрация акцепторов (например, атомов In), тем меньшая средняя плотность энергии электронов в зоне проводимости полупроводника, тем меньше средняя энергия на один электрон, и тем меньшая энергия требуется электрону, чтобы перейти в зону проводимости. Потому уровень Ферми находится ниже средины запрещенной зоны. 3. Кристаллическая структура полупроводника: описание структуры кристаллов
Кристалл можно представить как периодически повторяющиеся в пространстве одинаковые элементарные структурные единицы - элементарные ячейки кристалла, состоящие из одного, в простейшем случае, или нескольких атомов каждая. Элементарная ячейка в общем случае имеет форму косоугольного параллелепипеда. Все расположенные в ней атомы принято называть базисом элементарной ячейки кристалла. Закономерности строения элементарной ячейки и базиса, в частности степень их симметричности определяет многие свойства кристалла, в первую очередь электрические, магнитные и механические. Описание структуры любого кристалла можно и принято проводить, охарактеризовав его элементарную ячейку. Выбранную элементарную ячейку характеризуют тремя векторами основных трансляций
Пространственную решетку обычно характеризуют тремя векторами Базис принято задавать, описав положения всех атомов в одной ячейке набором радиус-векторов
4. Кристаллическая структура полупроводника: основные типы кристаллической решетки Типы кристаллических решеток. С помощью теории групп было показано, что все многообразие кристаллов может быть описано с помощью 14 типов кристаллических решеток (решеток Браве). Их принято группировать в семь систем, различающихся видом элементарной ячейки: триклинную, моноклинную, ромбическую, тетрагональную, тригональную, гексагональную и кубическую. Каждая система имеет свои соотношения между величинами
5. Кристаллическая структура полупроводника: направление и кристаллографические плоскости в кристаллической решетке Направление в кристаллической решетке задают координатами их направляющего вектора в базисных векторах
В кристалле большое значение имеют особые кристаллографические плоскости, проходящие через узлы кристаллической решетки. Именно кристаллографические плоскости, на которых расположено большое количество узлов кристаллической решетки, важны как для предсказания огранки кристалла, так и при рассмотрении движения частиц в нем). Кристаллографические плоскости принято описывать индексами Миллера - набором трех целых чисел, заключенных в круглые скобки
6. Кристаллическая структура полупроводника: дефекты кристаллической решетки
Дефектами кристалла называют всякое нарушение трансляционной симметрии кристалла — идеальной периодичности кристаллической решётки. Различают несколько видов дефектов по размерности. А именно, бывают нульмерные (точечные), одномерные (линейные), двумерные (плоские) и трёхмерные (объемные) дефекты. К нульмерным (или точечным) дефектам кристалла относят все дефекты, которые связаны со смещением или заменой небольшой группы атомов (собственные точечные дефекты), а также с примесями. Они возникают при нагреве, легировании, в процессе роста кристалла и в результате радиационного облучения. Одномерные (линейные) дефекты представляют собой дефекты кристалла, размер которых по одному направлению много больше параметра решетки, а по двум другим — соизмерим с ним. Двумерные. Основной дефект-представитель этого класса — поверхность кристалла. Другие случаи — границы зёрен материала, Трехмерные. Объёмные дефекты. К ним относятся скопления вакансий, образующие поры и каналы;
7. Температурная зависимость концентрации носителей Выражения, полученные для случая примесного проводника (см. выражения для положения уровня ферми для полупроводников n-типа) основаны на предположении, концентрация примесей существенно превышает собственную концентрацию полупроводника. Однако собственная концентрация экспоненциально зависит от температуры. Поэтому возникает вопрос о характере температурной зависимости концентрации носителей тока, поскольку она определяет температруную зависимость параметров параметров полупроводниковых приборов. В примесном полупроводнике свободные носители зарядов образуются за счет ионизации как примесных, так и собственных атомов, однако для ионизации собственных атомов и перевода электронов из валентной зоны в зону проводимости требуется энергия равная ширине запрещенной зоны, в то время, как для перевода электрона с уровня примеси в зону проводимости требуется многократно меньше энергии (см. зонные диаграммы полупроводников n иpтипов). Поэтому при каждой данной температуре вклад этих процессов в концентрацию СНЗ различен и зависит от температуры.
Температурные зависимости имеют три характерные области. В области низких температур, где средняя энергия тепловых колебаний решётки мала по сравнению с энергией ионизации донорной примеси, доноры ионизированы лишь частично. Концентрация свободных электронов незначительна, но экспоненциально растёт с увеличением температуры по мере ионизации доноров. Основную роль играют переходы электронов в зону проводимости с примесных уровней. С повышением температуры средняя энергия фононов сравнивается с энергией ионизации доноров, оставаясь, однако, значительно меньше ширины запрещённой зоны. В этой области температур практически все атомы донорной примеси ионизированы, и их электроны находятся в зоне проводимости. Вместе с тем средняя энергия тепловых колебаний ещё недостаточна для того, чтобы перебрасывать электроны из валентной зоны в зону проводимости и повышать концентрацию носителей за счёт переходов «зона–зона». С этого момента и до температур, при которых энергия тепловых колебаний практически сравнивается с шириной запрещённой зоны, дальнейшее повышение температуры не приводит к заметному увеличению концентрации электронов. Такое состояние полупроводника называется состоянием примесного истощения в том смысле, что примесные уровни «истощились», отдав свои электроны в зону проводимости. В области этих температур, протяжённостью в несколько сотен градусов абсолютной шкалы, концентрация ОНЗ-электронов практически не зависит от температуры (рис. 1.17) и равна концентрации доноров
Выполняются условия, использованные ранее для расчёта концентрации носителей (1.24), (1.25) в примесном полупроводнике. Остающаяся некоторая температурная зависимость концентрации обязана фактам ионизации собственных атомов решётки. Однако она незначительна, т. к. собственная концентрация Состояние примесного истощения, важное своей температурной стабильностью концентрации основных носителей заряда, наступает тем раньше, чем меньше концентрация примеси и ниже энергия её ионизации. В зависимости от характера примеси нижняя граница температур (начальная температура) примесного истощения может составлять несколько десятков градусов абсолютной шкалы, т. е. сотни градусов отрицательных температур шкалы Цельсия. В области более высоких температур средняя энергия фононов начинает превышать ширину запрещённой зоны. Концентрация СНЗ (1.18б) экспоненциально растёт. Ионизация собственных атомов создаёт пару СНЗ приобретает свойства собственного.
Область температур примесного истощения заканчивается, и состояние собственной проводимости наступает тем позже, чем выше концентрация примеси и шире запрещённая зона (рис. 1.17, рис. 1.18). Примесная проводимость уступает место биполярной собственной проводимости.
8. Процессы генерации и рекомбинации в полупроводниках и диэлектриках
Образование свободных носителей зарядов в п/п, связанных с переходом электронов из валентной зоны в зону проводимости. Для осуществления такого перехода электрон должен получить энергию достаточную для преодоления запрещенной зоны. Эту энергию электрон получает от ионов решетки совершающих тепловые колебания. Концентрация носителей заряда, вызванная термическим возбуждением в состоянии теплового равновесия называется равновесной. Однако помимо теплового возбуждено с другими причинами: в результате облучения фотонами или частицами большой энергии, ударной ионизации, введения носителей заряда в п/п из другого тела (инжекция) и т.д. Возникшие т.о. избыточные носители назыв. Неравновесными. Т.о. полная концентрация носителей зарядов: !!формулки Если возбуждение избыточным электронов из валентной зоны, а п/п однородный то ∆n=∆p. После прекращения действия механизма вызвавшего появление неравновесной концентрации носителей происходит постепенное возвращение к равновесному состоянию. Процесс установления равновесия заключается в том, что каждый избыточный электрон при встрече с вакантным местом (дыркой) занимает его, в результате чего пара неравновесных носителей исчезает. Явление исчезновения пар носителей получила название – рекомбинация. В свою очередь возбуждение электрона из валентной зоны или примесного уровня, сопровождающееся появлением дырки, назыв. – генерацией носителей заряда. !рисунок Скорость рекомбинации К пропорциональна концентрации СНЗ !формула Где ψ – коэффициент рекомбинации. При отсутствии освещения!формула, n0 и p0 – тепловые концентрации свободных электронов и дырок. !формула G0 – будет больше в узкозонных п/п и при высоких температурах. Если в п/п нет электрического тока, то изменение во времени неравновесной концентрации электронов и дырок в зонах определяется уранением: !формула
Где ∆G – это тмпераура генерации электронов и дырок за счет освещения п/п. !ФОРМУЛЫ Рассмотрим процесс рекомбинации неравновесных носителей зарядов (при отключении освещения в момент t=0) Рассмотрим 2 частных случая: 1.в собственном п/п при сильном освещении ∆n>>n0+p0 !формула ∆n0 – начальная концентрация неравновесных носителей заряда. Спадконцентраций происходит по параболическому закону
2.в донорном п/п в случае полной ионизации доноров !ФОРМУЛЫ ФОРМУЛЫ Τn – имеет смысл среднего времени жизни электрона в зоне проводимости
!рисунок спад неравновесной концентрации электрона во времени в донорном п/п. Среднее время жизни представляет собой такой отрезок аремени за который концентрация избыточных носителей изменится в «е» раз. Неравновесные носители заряда появляются только в том случае, если энергия фотонов при освещении п/п превышает ширину запрещенной зоны hυ>Eg
9. Зонная теория твердых тел(ЗТТТ) ЗТТТ позволила с единой точки зрения истолковать существование Ме диэлектриков и п/п, объясняя различие в их электрических свойствах: 1.неодинаковом заполнении электронами запрещенных зон 2.шириной запрещенных зон Степень заполнения электронами энергетических уровней в зоне определяется заполнением соответствующих атомных уровней, если при какой-то энергетический уровень полностью заполнен, то образующаяся энергетическая зона так же заполнена целиком. В общем случае можно говорить о валентно зоне, которая полностью заполнена электронами и образована их энергетических уровней внутренних электронов свободных атомов и о зоне проводимости (свободной зоне), которая либо частично заполнена электронами, либо свободна и образована из энергетических уровней внешних электронов изолированных атомов. В зависимости от степени заполнения зон электронами и шарины запрещенной зоны возможно 4 случая: !рисунок А)для Ме Б)для Ме В)для диэлектрика Г)для п/п На рис а) самая верхняя зона, содержащая электроны заполнена лишь частично, т.е. в ней имеются вакантные уровни. В данном случае электрон получив сколь угодно малую энергетическую добавку (за счет теплового движения энергетического поля) сможет перейти на более высокий уровень той же зоны, т.е. стать свободным и участвовать в проводимости. Если в твердом теле имеется зона лишь частично заполненная электронами, то это тело всегда будет проводником эл. Тока именно это свойственно Ме. Твердое тело является проводником эл. Тока и в том случае когда валентная зона перекрывается свободной зоной, что в конечном счете приводит к не полностью заполненной зоне (случай б). Это имеет место для щелочно-земельных элементов(2 группа). Образуется «гибридная» зона, которая заполняется валентными электронами лишь частично. Это приводит к тому что в данном случае металлические свойства щелочно-земельных элементов обусловлено перекрытием валентной и свободной зоны. Помимо рассмотренного перекрытия зон возможно так же перераспределение электронов между зонами, возникающие из уровней различных атомов, которое может привести к тому, что вместо 2х частично заполненных зон в кристалле окажется одна полностью заполненная(валентная) зона и одна свободная(проводимости) зона. Твердые тела у которых энергетический спектр электронных состояний состоит только из валентной зоны и зоны проводимости являются диэлектриками и п/п в зависимости от ширины запрещенной зоны. Если ширина запрещенной зоны кристалла порядка нескольких эВ, то тепловое движение не может перебросить электроны из валентной зоныв зону проводимости и кристалл является диэлектриком при всех реальных температурах(рис в). Если запрещенная зона достаточно узкая, то переброс электронов из валентной з. в з. проводимости может быть осуществлена сравнительно легко: путем теплового возбуждения, либо за счет внешнего источника способного передать электрону энергию ∆Е, в этом случае кристалл является п/п(рис г). Различие между Ме и диэлектриками с точки зрения зонной теории состоит в том, что при температуре 0К в зоне проводимости Ме присутствуют электроны, а в зоне проводимости диэлектриков они отсутствуют. Различие между диэлектриками и п/п определяется шириной запрещенной зоны: Для диэлектриков широка(пр. NaCl ДЕ=6эВ). Для п/п узкая(пр. Ge ДЕ=0.726). При температурах близких к 0К п/п ведут себя как диэлектрики, т.к. переброса электронов в з. проводимости не происходит. С увеличением температуры у п/п растет число электронов, которые в следствии теплового возбуждения переходят в зону проводимости, т.е. эл. Проводимость увеличивается. P-n переход и его свойства
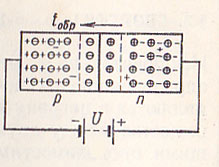
p-n -Перехо́д или электронно-дырочный переход — область пространства на стыке двух полупроводников p- и n-типа, в которой происходит переход от одного типа проводимости к другому.
Определяющее свойство р-n-перехода – его односторонняя проводимость. Упрощенно механизм односторонней проводимости можно объяснить следующим образом, рисунок ниже:
Так как в области р с дырочной проводимостью подвижных электронов значительно меньше, чем в области п с электронной проводимостью, то электроны из n-слоя начинают переходить в р-слой (у их границы), а дырки в то же время будут двигаться в обратном направлении. При этом электрическая нейтральность каждой области окажется нарушенной. В пограничном слое с проводимостью типа а образуется положительный объемный заряд, а в р-области, то есть по другую сторону границы,— отрицательный. Таким образом, в тонком слое полупроводника у границы раздела р- и n-областей образуются две зоны объемных разноименных электрических зарядов. Этот слой и представляет собой собственно р-n-переход. Естественно, возникновение разноименных зарядов влечет за собой появление электрического поля. Это поле препятствует проникновению электронов в р-область, а дырок в «-область, причем настолько эффективно, что лишь отдельные электроны и дырки, обладающие повышенной энергией, могут преодолевать его тормозящее действие. Наступает стабильное состояние р-n-перехода. Если к полупроводнику приложить электрическое напряжение, то в зависимости от полярности этого напряжения р-n-переход проявляет совершенно различные свойства. Когда отрицательный полюс источника подключен к n-области кристалла, а положительный — к р-области:
внешнее электрическое поле и поле р-n-перехода направлены в противоположные стороны. Поэтому электрическое поле р-n-перехода окажется в значительной степени ослабленным, и теперь уже электроны из n-области смогут проникать в р-область, а дырки из р-области в n-область. Таким образом, в цепи источник питания — полупроводник возникает ток. Полярность приложенного напряжения, при которой через полупроводник протекает ток (как в описанном случае), получила название прямой полярности. Когда же отрицательный полюс источника питания подключен к р-области кристалла, а положительный к n-области:
электрические поля источника и р-n-перехода совпадают. Суммарное поле возрастает и в еще большей степени (чем до присоединения источника питания) будет препятствовать передвижению электрических зарядов через р-n-переход. Если рассматривать идеальный случай, то электрического тока через переход не будет. Такую полярность приложенного к кристаллу напряжения называют обратной. Итак, с определенной долей приближения можно считать, что электрический ток через р-n-переход протекает, если полярность напряжения источника питания прямая, и, напротив, тока нет, когда полярность обратная.
Эффективность излучения.
Поскольку рекомбинация в полупроводниках может быть как излучательной, так и безызлучательной, то эффективность излучения зависит от конкурентоспособности этих процессов. Критерием эффективности является внутренний квантовый выход, который определяется как отношение числа актов излучательной рекомбинации к полному числу актов (излучательных и безлучательных). Если PR, PNR – вероятности излучательной и безызлучательной рекомбинации, отнесенные к единице времени, то внутренний квантовый выход nj определяется следующим выражением:
Следовательно, для получения максимального njнеобходимо увеличить отношение вероятностей излучательной вероятности к безызлучательной. Вероятность безызлучательной рекомбинации можно уменьшить путем снижения в полупроводниковом материале концентрации неконтролируемых примесей и структурных дефектов, играющих роль центров безызлучательной рекомбинации.
25. Виды люминесценции. Релаксация люминесценции
У твёрдых тел различают три вида люминесценции:
1). мономолекулярная люминесценция — акты возбуждения и испускания света происходят в пределах одного атома или молекулы;
2). метастабильная люминесценция — акты возбуждения и испускания света происходят в пределах одного атома или молекулы, но с участием метастабильного состояния;
3). рекомбинационная люминесценция — акты возбуждения и испускания света происходят в разных местах.
26. Поглощение излучения в полупроводниках. Основные электронные переходы при поглощении света в кристаллах Интенсивность света, проходящая через вещество, постепенно уменьшается. Поглощение электромагнитного излучения твердым телом осуществляется различными путями: 1. Энергия излучения расходуется на перевод электронов в более высокое энергетическое состояние; 2. Энергия электромагнитного поля передается кристаллической решетке и превращается в тепло. 3. Возможные переходы электронов в кристаллах под действием света
Переход 1 приводит к появлению электронов в зоне проводимости и, соответствующему собственному (фундаментальному) поглощению. В момент возникновения созданные светом носители заряда могут и не находиться в тепловом равновесии с кристаллической решеткой, однако вследствие взаимодействия с ней эти носители быстро (10-10 с) передают решетке свою избыточную энергию. Поэтому распределение по энергии избыточных и основных носителей заряда будет одинакова. При поглощении света твердым телом возможно и такое возбуждение электрона в валентной зоне, при котором он не переходит в зону проводимости и образует с дыркой связанную кулоновскими силами систему (переход 2). Такая система называется экситоном. В предположении слабого взаимодействия, когда экситоны велики по сравнению с постоянной решеткой кристалла, экситон можно представить как электрон и дырку, связанную кулоновскими силами и медленно двигающимися по большим орбитам относительно их центра масс. Экситоны могут локализоваться возле различных дефектов кристаллической структуры. Они являются нейтральными образованиями и их появление не приводит к изменению электрических характеристик образца. Если температура достаточно высока, чтобы под действием тепловой энергии экситонный электрон смог перейти в зону проводимости, то конечным итогом будет тот же результат, что и в случае перехода 1. При этом энергия фотона При поглощении кванта света возможен переход электрона с акцепторного на свободный донорный уровень ДАП (переход 5). Зависимость кулоновского взаимодействия между донором и акцептором от межатомного расстояния между ними задает целый ряд значений энергии такого поглощения.
ΔE – ширина запрещенной зоны, Edи Ea – энергии ионизации донора и акцептора, q–заряд электрона, Расстояние между линиями поглощения ДАП определяется, таким образом, дискретными положениями дефектов в кристаллической решетке. Переходы 1, 3, 4 изменяют электропроводность кристалла, на этом явлении внутреннего фотоэффекта основана работа многих фотоприемников. При внутрицентровых переходах 6 электрон не освобождается и процесс поглощения света не приводит к изменению электропроводности. То же относится и к экситонному поглощению, переходу в ДАП и поглощению свободными носителями заряда (переход 7) в более характерному для металлов. Экспериментально установлено, что уменьшение потока излучения при его поглощении в среде толщиной dl пропорционально пути и потоку падающего излучения:
α – коэффициент пропорциональности – показатель поглощения (не путать с коэффициентом поглощения, который представляет собой отношение потока излучения поглощенного телом к потоку излучения, упавшего на тело). Закон Бугера-Ламберта:
Таким образом, показатель поглощения α – величина, обратная расстоянию l, на котором поток излучения уменьшается ~2,7 раза. Зависимость показателя α от длины волны падающего света называется спектром поглощения вещества.
Собственное поглощение начинается при частоте ν0, на краю которого при низких температурах хорошо проявляется структура экситонного поглощения света (переходы 1 и 2). Примесное поглощение создает полосы с 3 по 6; в широком диапазоне частот присутствует слабое поглощение света свободными носителями заряда (полоса 7) и, наконец, при малых энергиях квантов излучения обычно хорошо выделяется участок 8, связанный с поглощением излучения кристаллической решетки (в этом случае световая энергия превращается в энергию колебания ионов).
27. Фотоэлектрические явления в полупроводниках: внутренний фотоэффект, фотопроводимость и ее релаксация Внутренний фотоэффект – изменение электрического сопротивления полупроводника, под действием излучения, называет фоторезистивным эффектом (или внутренним). Добавочная проводимость обусловленная носителями заряда созданным оптической генерацией носит название фотопроводников. При внутреннем фотоэффекте первичным актом является поглощение фотонов, поэтому процесс образования свободных носителей зарядов будет происходить по разному в зависимости от особенностей процесса поглощения света полупроводников.
При межзонных переходах имеет место собственная фотопроводимость, при наличии запрещённой зоны полупроводника, локальных уровней, оптическое поглощение может вызывать переходы электронов между уровнями примесей и энергетическими зонами переходы 2 и 3. В этом случае фотопроводимость называют примесной. Поглощение света свободными носителями заряда и колебаниями решётки, непосредственно не могут привести к изменению концентрации носителей заряда, однако возрастание концентрации носителей заряда может происходить в результате вторичных дефектов, тогда поглощение света значительно увеличивает кинетическую энергия SnZкоторая затем отдает свою энергию на возбуждение носителей зарядов. Фотопроводимость – избыточные электроны
Коэффициент пропорциональности b называется квантовым выходом фото- ионизации, который определяет число пар носителей заряда (или число носи- телей заряда при примесной фотопроводимости), образуемых одним погло- щенным фотоном, если интенсив
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 4555; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.136.23.84 (0.019 с.) |


 )
) - эффективная плотность состояний в зоне проводимости
- эффективная плотность состояний в зоне проводимости
 – эффективная плотность состояний в валентной зоне
– эффективная плотность состояний в валентной зоне
 и
и  ). В этом случае уравнение механики
). В этом случае уравнение механики ,
, 
 в эти уравнения поставить эффективную массу электрона
в эти уравнения поставить эффективную массу электрона 


 совпадающими с ее тремя ребрами, сходящимися в одной точке. Две точки с радиус-векторами
совпадающими с ее тремя ребрами, сходящимися в одной точке. Две точки с радиус-векторами  и
и  , связанные соотношением
, связанные соотношением  , где
, где  - целые числа, описывают одну и ту же точку базиса, но в разных элементарных ячейках кристалла. В таком случае удобно подробно охарактеризовать расположение атомов базиса в пределах одной элементарной ячейки, а всю структуру кристалла получить трансляцией - "тиражированием" данной ячейки, осуществляя параллельные переносы на векторы
- целые числа, описывают одну и ту же точку базиса, но в разных элементарных ячейках кристалла. В таком случае удобно подробно охарактеризовать расположение атомов базиса в пределах одной элементарной ячейки, а всю структуру кристалла получить трансляцией - "тиражированием" данной ячейки, осуществляя параллельные переносы на векторы  , называемые векторами трансляций. Можно сказать, что для полного описания структуры кристалла достаточно задать: 1) пространственную решетку, получаемую путем параллельных переносов на все векторы
, называемые векторами трансляций. Можно сказать, что для полного описания структуры кристалла достаточно задать: 1) пространственную решетку, получаемую путем параллельных переносов на все векторы  одной точки и 2) базис.
одной точки и 2) базис. называемые периодами кристаллической решетки и углы
называемые периодами кристаллической решетки и углы  между ними; именно эти параметры обязательно содержатся во всех справочниках по структуре веществ [2,3].
между ними; именно эти параметры обязательно содержатся во всех справочниках по структуре веществ [2,3]. , числа
, числа  задают положения атомов в долях соответственно векторов
задают положения атомов в долях соответственно векторов  .
. и
и  . Некоторые из этих решеток имеют разновидности: примитивная -
. Некоторые из этих решеток имеют разновидности: примитивная -  , объемноцентрированная (ОЦ) -
, объемноцентрированная (ОЦ) -  , гранецентрированная (ГЦ) -
, гранецентрированная (ГЦ) -  и с одной парой центрированных противоположных граней -
и с одной парой центрированных противоположных граней - 
 ,
,  ,
,  и
и  . Для описания такого семейства направлений используют треугольные скобки
. Для описания такого семейства направлений используют треугольные скобки  .
. . Знак минус отрицательного индекса принято ставить над ним. Эти индексы имеют простой геометрический смысл. Если вдоль трех координатных осей, заданных векторами
. Знак минус отрицательного индекса принято ставить над ним. Эти индексы имеют простой геометрический смысл. Если вдоль трех координатных осей, заданных векторами  , отложить соответственно отрезки с длинами
, отложить соответственно отрезки с длинами  (см. рис. 1.5), то получившиеся три точки однозначно зададут проходящую через них плоскость
(см. рис. 1.5), то получившиеся три точки однозначно зададут проходящую через них плоскость  . На рис. 1.6 показаны плоскости
. На рис. 1.6 показаны плоскости  . Заметим, что параллельно изображенной на рис. 1.5 плоскости можно провести много параллельных плоскостей проходящих через узлы кристаллической решетки, откладывая по осям отрезки с длинами
. Заметим, что параллельно изображенной на рис. 1.5 плоскости можно провести много параллельных плоскостей проходящих через узлы кристаллической решетки, откладывая по осям отрезки с длинами  (
( - целое число) расстояние между такими ближайшими плоскостями называется межплоскостным расстоянием
- целое число) расстояние между такими ближайшими плоскостями называется межплоскостным расстоянием  системы плоскостей
системы плоскостей  . Величину
. Величину 



 .
. Примесный полупроводник
Примесный полупроводник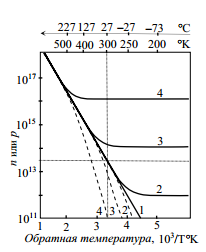

 Верхняя граница – максимальная (конечная) температура состояния примесного истощения Tmax – определяется как температура, при которой собственная концентрация сравнивается с концентрацией легирующейпримесиni=ND. На рис. приведены зависимости Tmax от степени легирования NдляGe (Eg = 0,72 эВ), Si (Eg = 1,12 эВ) и GaAs (Eg = 1,43 эВ).
Верхняя граница – максимальная (конечная) температура состояния примесного истощения Tmax – определяется как температура, при которой собственная концентрация сравнивается с концентрацией легирующейпримесиni=ND. На рис. приведены зависимости Tmax от степени легирования NдляGe (Eg = 0,72 эВ), Si (Eg = 1,12 эВ) и GaAs (Eg = 1,43 эВ).



 , могут происходить переходы электронов с локальных уровней примесей или собственных дефектов в зону проводимости (переход 3) или из валентной зоны на эти уровни (переход 4). Если кристаллы содержат в равных и достаточно больших количествах как донорные, так и акцепторные дефекты, то возможна ситуация, когда доноры и акцепторы будут находиться недалеко друг от друга, порядка 10 нм и меньше. В этом случае будет иметь место перекрытие электронных орбит донора, акцептора, которое образует так называемые донорно-акцепторные пары (ДАП).
, могут происходить переходы электронов с локальных уровней примесей или собственных дефектов в зону проводимости (переход 3) или из валентной зоны на эти уровни (переход 4). Если кристаллы содержат в равных и достаточно больших количествах как донорные, так и акцепторные дефекты, то возможна ситуация, когда доноры и акцепторы будут находиться недалеко друг от друга, порядка 10 нм и меньше. В этом случае будет иметь место перекрытие электронных орбит донора, акцептора, которое образует так называемые донорно-акцепторные пары (ДАП).
 - статическая диэлектрическая проницаемость среды,
- статическая диэлектрическая проницаемость среды,  - постоянная.
- постоянная.



 созданные оптической генерацией, могут иметь энергии значительно большие чем средняя энергия равновесных носителей заряда, однако в результате взаимодействия с дефектами кристаллической решётки энергия неравновесных носителей зарядов, за время
созданные оптической генерацией, могут иметь энергии значительно большие чем средняя энергия равновесных носителей заряда, однако в результате взаимодействия с дефектами кристаллической решётки энергия неравновесных носителей зарядов, за время  приобретает такое распределение по энергии, как у равновесных носителей, поэтому подвижность неравновесных носителей зарядов не будет отличаться от подвижности равновесных зарядов, следовательно полная проводимость полупроводника определяется равновесными носителями зарядов
приобретает такое распределение по энергии, как у равновесных носителей, поэтому подвижность неравновесных носителей зарядов не будет отличаться от подвижности равновесных зарядов, следовательно полная проводимость полупроводника определяется равновесными носителями зарядов  и фото носителями
и фото носителями 




