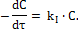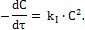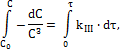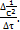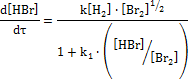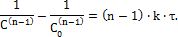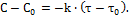Кинетические уравнения для простых реакций

 

Скорость одной и той же химической реакции может существенно меняться в зависимости от концентрации исходных веществ (реагентов), а также вследствие изменения концентрации реагирующих веществ в ходе реакции. Поэтому для характеристики химического процесса удобнее использовать константу скорости химической реакции (k), которая зависит только от природы веществ, температуры, наличия (или отсутствия) катализатора, но не зависит от концентрации исходных веществ.

Решить кинетическое уравнение – это значит найти простую, удобную для использования, аналитическую форму зависимости между концентрацией и временем протекания химической реакции (решается методом интегрирования).

Рассмотрим способы решения кинетических уравнений для простых реакций.

1) Мономолекулярные реакции (реакции I порядка)

Стехиометрическое уравнение реакции имеет вид:

А → продукты

Кинетическое уравнение первого порядка имеет вид:

Решение этого уравнения (методом интегрирования) приводит к следующему аналитическому выражению для реакции первого порядка:

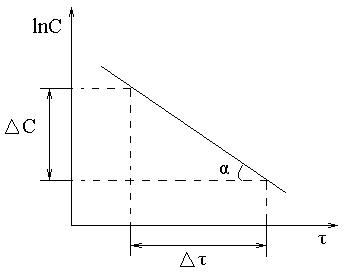
lnC = lnC₀ – k_I∙τ,

где C – концентрация, установившаяся к началу времени τ, моль/л;

C₀ – начальная концентрация, моль/л;

τ – время протекания реакции, с.

Если на основании опытных данных построить график в коорди-натах lnC–τ, то получим прямую линию (рисунок 1).

Рисунок 1 – Зависимость lnC от τ для реакций первого порядка

 

Тангенс угла наклона данной прямой равен константе скорости:

tg α = k_I=

Размерность константы:

2) Бимолекулярные реакции (реакции II порядка)

Стехиометрические уравнения могут быть двух типов:

I А + A → продукты

II A + B → продукты

Рассмотрим решение для уравнений первого типа. Кинетическое уравнение для ракции данного типа имеет вид:

После интегрирование получим:

Если на основании опытных данных построить график в коор-динатах 1/C–τ, то получим прямую (рисунок 2).

Рисунок 2 – Зависимость 1/C от τ для реакций второго порядка

 

Тангенс угла наклона данной прямой равен константе скорости:

tg α = k_II=

Размерность константы:

3) Тримолекулярные реакции (реакции III порядка)

Стехиометрические уравнения третьего порядка могут быть соответственно трех типов:

I A + A+ A → продукты

II A + A + B → продукты

III A + B + D → продукты

Рассмотрим, как и в случае бимолекулярных реакций, наиболее простой случай – реакции первого типа. Кинетическое уравнение для такой реакции будет иметь вид:

После интегрирования получим:

Если на основании опытных данных построить график в коорди-натах 1/C²–τ, то получим прямую (рисунок 3).

Рисунок 3 – Зависимость 1/C² от τ для реакций третьего порядка

 

Тангенс угла наклона данной прямой равен константе скорости:

tg α = k_III=

Размерность константы:

Константы, имеющие разные размерности, сравнивать нельзя.

 

Кинетические уравнения для сложных реакций

 

Кинетическое уравнение многостадийной реакции может быть довольно сложным. Так, для реакции Н₂ + Вr₂ → 2НВr скорость взаимодействия брома с водородом описывается уравнением

Однако в ряде случаев, когда скорости отдельных стадий несоизмеримы (одна из стадий является лимитирующей), удается получить довольно простые кинетические уравнения, аналогичные уравнениям для одностадийных реакций. Так, скорость реакции дробного порядка для одного вещества описывается уравнением

Интегрирование приводит к выражению

Кинетическое уравнение нулевого порядка имеет вид:

После интегрирования получают

Встречаются многостадийные реакции, уравнение скорости для которых имеет общий второй или третий порядок.

 

Расчет порядка реакции и константы скорости реакции

По экспериментальным данным

 

Существует достаточно много экспериментальных методов определения порядка и константы скорости реакции. В данной работе используется так называемый «метод изоляции», сущность которого заключается в поочередном изменении концентрации каждого вещества, участвующего в реакции при постоянной концентрации других веществ. Постоянство состава достигается тем, что концентрации этих веществ берут в большом избытке (в 10–20 раз больше), чем это требуется в соответствии со стехиометрическим уравнением. Затем измеряют время протекания реакции при каждой данной концентрации вещества.

Расчет порядка реакции по данному веществу производят одним из следующих способов.

1) Первый способ. Часто порядок реакции по веществу равен 1, 2 или 3. Поэтому целесообразно проверить, какая из зависимостей: lnС–τ, 1/C–τ или 1/C²–τ будет линейной (см. рисунки 1, 2, 3). Если, например, линейной окажется зависимость lnС–τ, то это означает, что порядок реакции по данному веществу равен 1, и т.д.

2) Второй способ. Данный способ удобен, если порядок реакции по веществу больше трех или является дробным числом. Расчет проводят в следующей последовательности:

– строят зависимость время–концентрация, откладывая значения концентраций на оси ординат, времени – на оси абсцисс;

– определяют скорость реакции для каждой заданной концентрации по тангенсу угла наклона касательной к кривой время–концентрация. Для проведения касательных можно использовать наиболее простой метод хорд, суть которого видна из рисунка 4;

Рисунок 4 – Графический метод нахождения скорости

по углу наклона касательной

 

– строят график lnW–lnC, откладывая на оси абцисс логарифм концентрации, на оси ординат – логарифм скорости (рисунок 5).

 

Рисунок 5 – Зависимость скорости от концентрации

в логарифмической шкале

 

Порядок реакции n равен тангенсу угла наклона прямой.

 

ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ

 

Описываемые ниже экспериментальные методы определения константы скорости и порядка реакции относятся к наиболее простому случаю, когда скорость реакции может быть выражена как произведение концентраций реагирующих веществ.