
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основной закон динамики материальной точки.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Уравнение В механике Ньютона масса не зависит от характеристик движения, времени. Записав ускорение как
Вектор Импульс это одна из важнейших динамических характеристик материальной точки В форме (**) основной закон динамики утверждает, что скорость изменения импульса материальной точки равна действующей на нее силе. В этом состоит (согласно современной терминологии) второй закон Ньютона. Основной закон динамики выражает принцип причинности в классической механике, т.е. устанавливает однозначную связь между изменением со временем состояния движения и положением материальной точки в пространстве и действующей на нее силой. Закон позволяет по начальному состоянию материальной точки: начальным координатам и скорости в начальный момент времени ( На основании обобщения опытных фактов был установлен важный принцип ньютоновской механики - принцип независимости действия сил: если на материальную точку одновременно действует несколько сил, то каждая из них, сообщает материальной точке такое же ускорение, как если бы других сил не было. Т.о.
Основной закон динамики можно переписать в виде:
Величину Т.о. из основного закона и принципа независимости действия сил следует, что изменение импульса материальной точки за малый промежуток времени
 , смотри рис.. , смотри рис..
Интеграл в правой части есть импульс силы за конечный промежуток времени
Если сила, действующая на материальную точку постоянная, то:
если Третий закон Ньютона Наблюдения и опыты свидетельствуют о том, что механическое действие одного тела на другое является всегда взаимодействием. Если тело 2 действует на тело 1, то тело 1 обязательно противодействует телу 2. Например, на ведущие колеса автомобиля со стороны шоссе действует сила трения покоя в сторону движения автомобиля, а колеса действуют на шоссе также с силой трения в противоположную сторону.
Взаимодействия двух тел друг на друга равны между собой по величине и направлены в противоположные стороны.
Силы взаимодействия всегда появляются парами. Обе силы приложены к разным телам и являются силами одной природы. В третьем законе предполагается, что обе силы равны по модулю в любой момент времени независимо от движения тел. Это соответствует ньютоновской механике, в которой взаимодействие распространяется мгновенно. Такое предположение называется принципом дальнодействия ньютоновской механики, согласно ему скорость распространения взаимодействия бесконечно большая. В действительности это не так, поэтому третий закон, а также второй имеют определенные границы применения. При Законы Ньютона являются основными законами. Из них могут быть выведены все остальные законы механики.
2.8. Преобразования Галилея
Подразумевается, что длины отрезков и ход времени не зависит от состояния движения и одинаковы в системах
Уравнения (1-5) называются преобразованиями Галилея. Продифференцировав их по времени, получим связь между скоростями точки А в системах отсчета
Эти формулы дают правила сложения скоростей в классической механике. Соотношение (6) справедливо и для произвольного выбора взаимных направлений координатных осей систем отсчета После второго дифференцирования получим с учетом того, что
т.е. ускорение точки во всех системах отсчета, движущихся равномерно и прямолинейно, оказывается одинаковым.
|
||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 887; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.104.211 (0.008 с.) |

 описывает изменение движения тела конечных размеров под действием силы при отсутствии деформации и если оно движется поступательно. Для точки это уравнение справедливо всегда, поэтому его можно рассматривать как основной закон движения материальной точки.
описывает изменение движения тела конечных размеров под действием силы при отсутствии деформации и если оно движется поступательно. Для точки это уравнение справедливо всегда, поэтому его можно рассматривать как основной закон движения материальной точки. и умножив на массу, получим:
и умножив на массу, получим:  или
или (**).
(**). равный произведению массы тела на его скорость называют импульсом материальной точки.
равный произведению массы тела на его скорость называют импульсом материальной точки. ) и действующей на нее силы рассчитать ее поведение в любой последующий момент времени.
) и действующей на нее силы рассчитать ее поведение в любой последующий момент времени. , где
, где  —результирующая сила;
—результирующая сила; (***)
(***) называют элементарным импульсом, вектор
называют элементарным импульсом, вектор  - элементарным импульсом силы за малый промежуток времени
- элементарным импульсом силы за малый промежуток времени  её действия.
её действия. Изменение импульса за конечный промежуток времени от
Изменение импульса за конечный промежуток времени от  до
до  можно найти интегрированием левой и правой частей уравнения (***)
можно найти интегрированием левой и правой частей уравнения (***)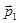


 .
. 
 ;
; то
то  ,
,  среднее значение силы за
среднее значение силы за  Количественное описание механического взаимодействия было дано Ньютоном в его третьем законе динамики.
Количественное описание механического взаимодействия было дано Ньютоном в его третьем законе динамики.
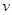 <<
<<  оба закона выполняются с очень большой точностью.
оба закона выполняются с очень большой точностью. Они позволяют определить кинематические величины при переходе от одной инерциальной системы отсчета к другой. Возьмем две системы отсчета, одна из которых К неподвижна, а вторая -
Они позволяют определить кинематические величины при переходе от одной инерциальной системы отсчета к другой. Возьмем две системы отсчета, одна из которых К неподвижна, а вторая -  движется относительно
движется относительно 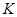 со скоростью
со скоростью  вдоль оси
вдоль оси  . Пусть начала координат систем совпадали при
. Пусть начала координат систем совпадали при 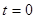 . Запишем соотношение между радиусами – векторами
. Запишем соотношение между радиусами – векторами  и
и  одной и той же точки
одной и той же точки 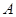 в
в  ; (1) Или в координатной форме:
; (1) Или в координатной форме: ; (2)
; (2) ; (3)
; (3) ; (4)
; (4) (5)
(5) .
. (6)
(6) (7)
(7) (8)
(8) (9)
(9) :
: ,
,


