
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оптимизация по Винеру и КалмануСодержание книги
Поиск на нашем сайте Если структурная схема РАС не определена, то синтез следящей системы целесообразно проводить по другому принципу. Предполагаем, что в процессе работы РАС ошибка слежения не выходит за пределы линейного участка дискриминационной характеристики. Более общей постановкой задачи синтеза оптимальных систем является постановка её с учётом достижения минимума функционала:
где Задача оптимального синтеза формулируется следующим образом: «из допустимого множества l(t) необходимо выбрать и технически реализовать такой сигнал управления, который переводит объект управления из начального состояния в конечное и минимизирует функционал (7.17)». РАС представляется в этом случае как линейный фильтр, с выхода которого снимается сигнал y(t). Доказано [1 – 5], что необходимым и достаточным условием оптимальности системы по критерию минимума СКО является отсутствие корреляции между мгновенной ошибкой оптимизируемой РАС и выходной величиной другой линейной системы [5]. При воздействии на систему гауссовского случайного процесса оптимальный линейный фильтр обладает наилучшими характеристиками. Для определения импульсной характеристики оптимального фильтра потребуется решить интегральное уравнение Винера – Хопфа при заданных корреляционных функциях воздействия и возмущения.
где r (t) = l(t) + x(t)/ Sд – смесь сигналов воздействия и помехи. Если не накладывать ограничений на ИХ и функцию возмущения (при этом может получиться физически не реализуемое решение), то решение (7.18) большой сложности не представляет.
Так как (7.19) соответствует интегралу свертки, удобно перейти с помощью преобразования Фурье в частотную область
На основании спектральных плотностей заданных процессов определяется ЧПФ РАС как фильтра. В качестве функционала в этом случае используется следующий интеграл:
где K (j ω) – характеристика эквивалентного фильтра разомкнутой системы; v – порядок астатизма.
Пример 7.5. Определить ИХ фильтра Винера без учета физической реализуемости обобщенной РАС, если известны спектральные плотности сигналов воздействия
Следующий этап – разложение (7.23) на сумму простых дробей
где Взяв обратное преобразование Фурье от (7.24), получим ИХ:
Очевидно, что такая ИХ не может быть физически реализована, так как ИХ существует в отрицательные моменты времени, то есть фильтр использует данные, которые реально еще не получены [18]. СКО данной РАС (при a = b = Sд = N0 = 1) составляет 0,58 [18]. Подобное решение, тем не менее, представляет определенный интерес, так как определяет нижнюю теоретическую границу СКО, а также может быть использовано в системах с накоплением информации (данные в отрицательные, то есть в предшествующие, моменты времени могут запоминаться в устройствах памяти системы). Чтобы полученное решение (7.18) было физически реализуемо, необходимо задать требования физической реализуемости для процессов воздействия и возмущения. При этом решение существенно усложняется. В процедуре решения выделяют следующие этапы [1 – 5]. 1. Спектральную плотность S l r (w) факторизуют:
то есть разлагают на комплексно-сопряженные функции Y(j w). 2. Функцию S lr(w)/Y(– j w) разлагают на элементарные дроби, а после этого оставляют дроби только с полюсами в левой комплексной полуплоскости. 3. Записывают выражение для ЧПФ в таком виде:
где в выражениях в квадратных скобках со знаком «*» оставляют дроби только с полюсами в левой комплексной полуплоскости. Если возмущение представляет собой белый шум, то процедура вычислений существенно упрощается (W (j w) – ЧПФ разомкнутой РАС).
Пример 7.6. Определить ИХ физически реализуемого фильтра Винера для обобщенной РАС для исходных данных примера 7.5 [5, 18].
где Выполним факторизацию (7.29):
Приступаем ко второму этапу, находим S lr(w)/Y(– j w)
а затем разлагаем на простые дроби:
где Выполняя действия по третьему этапу в результате получаем [5]:
где Остается определить ИХ с помощью формул из прил. 1:
График ИХ (7.34) представлен на рис. 7.15.
СКО данной РАС При a = b = Sд = N0 = 1 Dx = 0,73 [18]. Таким образом, дополнительное ограничение на ИХ оптимального фильтра приводит к увеличению СКО.
Имея результат (7.33), можно определить K2 (p) в контуре управления обобщенной РАС (рис. 3.1).
где в данном примере При изменении уровня помехи в данном случае достаточно будет подстраивать только k2 для минимизации СКО.
Кроме того, в РАС существует необходимость достигать минимум СКО не только в установившемся режиме, но и в определенный момент времени наблюдения. Поэтому решение интегрального уравнения, аналогичного (7.18), существенно усложняется, как и практическая реализация после фильтра [2, 5, 18]. В 1960 г. Р. Калман [18] предложил альтернативную формулировку задачи оптимальной фильтрации по критерию наименьших квадратов. Фильтр Калмана обеспечивает минимум СКО в произвольный момент времени и успешно работает при нестационарных входных воздействиях. Для решения сформулированной задачи Калман использовал методы пространства состояний. Отметим характерные черты, которые отличают формулировку задачи оптимальной фильтрации по Калману. 1. В фильтрации по Винеру случайные процессы характеризуются их корреляционными функциями. По Калману случайные процессы моделируются системой дифференциальных уравнений первого порядка относительно переменных, которые характеризуют состояние процесса в любой момент времени. Эти переменные называются переменными состояния, а их совокупность – вектором состояния. 2. В методе Винера оптимальная оценка задающего воздействия находится как выходная величина линейного фильтра, ИХ которого удовлетворяет некоторому интегральному уравнению. В методе Калмана оптимальная оценка находится как решение дифференциального уравнения, коэффициенты которого определяются статистикой процесса [18]. Пример 7.7. Определить оптимальный физически реализуемый фильтр Калмана при исходных данных примера 7.5 [1, 2, 5].
После получения характеристики формирующего фильтра записываются матрицы пространства состояний [2]. После сложных вычислений, которые можно найти в [1, 2, 5], получается структурная схема, представленная на рис. 7.17. Параметры элементов схемы таковы [2]:
Дисперсия ошибки определяется по следующей формуле [2]:
В [2] показано, что при переходе к установившемуся режиму получаются такие же значения, что и в выше рассмотренном примере 7.6. Кроме того, в [2] доказывается, что за счет переменных параметров фильтра в данном случае достигается выигрыш в качестве регулирования порядка 15%.
Если спектральные плотности процессов воздействия и возмущения известны, то можно так приближенно определить оптимальную полосу пропускания РАС (рис. 7.18) [1]. Если процессы некоррелированы, то оптимальная полоса пропускания РАС (w опт) соответствует верхней частоте спектра сигнала воздействия (Sl)(рис. 7.18 а). Если возмущение представляет собой белый шум (Sш), то полоса пропускания РАС также определяется полосой пропускания по воздействию (Sl) (рис. 7.18 а). Если процессы имеют связь, то графики спектральных плотностей S λ(ω) и S x(ω) проникают друг в друга (рис. 7.18 б), и в этом случае оптимальное значение полосы пропускания РАС (w опт) с минимальной СКО находится в точке пересечения графиков [1]. Если процессы воздействия и возмущения имеют закон распределения, отличный от нормального, то оптимальную систему определяют с помощью методов теории нелинейной оптимальной фильтрации [18]. Список рекомендуемой литературы: [ 1, с. 104-142, 235-238; 2, с. 157-171; 3, с. 252-273, 338-374; 4, с. 114-139, 141-162; 5, с. 177-191; 6, с. 22-25; 8; 10, т. 1, с. 237-244, 254-258, 268-274; 10, т. 2, с. 209-218; 11, с. 625-652; 13, с. 138-152, 411-422; 17, 18, с. 95-115]. Контрольные вопросы 1. В чем заключается инженерный метод синтеза РАС? 2. Опишите последовательность инженерного синтеза РАС по заданной ЛАЧХ. 3. Дайте определение желаемой и неизменяемой ЛАЧХ. 4. Опишите последовательность инженерного синтеза РАС по заданной желаемой и неизменяемой асимптотической ЛАЧХ. 5. Для чего применяются корректирующие устройства? 6. Опишите основные разновидности корректирующих устройств, их способы включения и их радиотехнические реализации. 7. Какой фильтр называют оптимальным для определенной РАС? 8. Опишите особенности фильтров Винера и Калмана. 9. Назовите условия физической реализуемости фильтров. 10. Опишите особенности фильтров Винера и Калмана. 11. Назовите основные критерии оптимизации РАС. 12. Как определяют ПФ оптимального фильтра для заданной РАС?
|
||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 69211; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.008 с.) |

 , (7.17)
, (7.17) для сигнала управления и помехи соответственно.
для сигнала управления и помехи соответственно.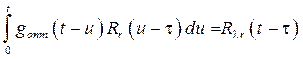 , (7.18)
, (7.18)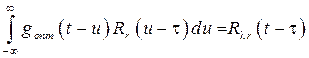 . (7.19)
. (7.19)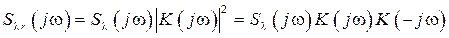 . (7.20)
. (7.20) , (7.21)
, (7.21) . (7.22)
. (7.22) и помехи
и помехи 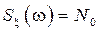 .
.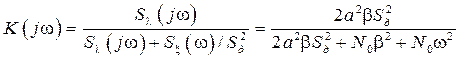 . (7.23)
. (7.23)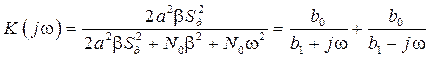 , (7.24)
, (7.24)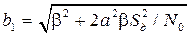 ,
, 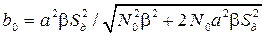 .
.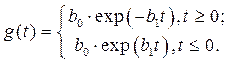 . (7.25)
. (7.25)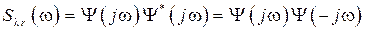 , (7.26)
, (7.26)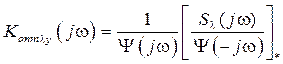 , (7.27)
, (7.27)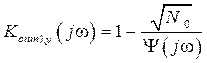 ,
,  . [5] (7.28)
. [5] (7.28)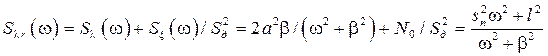 , (7.29)
, (7.29) – спектральная плотность помехи, приведенная ко входу дискриминатора;
– спектральная плотность помехи, приведенная ко входу дискриминатора; 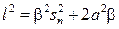 [5].
[5].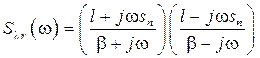 ,
, 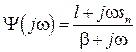 ,
, 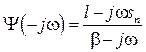 . (7.30)
. (7.30) , (7.31)
, (7.31)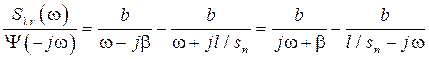 , (7.32)
, (7.32)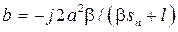 , и оставляем только первое слагаемое (у второго слагаемого правый корень).
, и оставляем только первое слагаемое (у второго слагаемого правый корень). , (7.33)
, (7.33)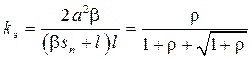 ,
, 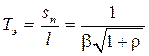 ;
; 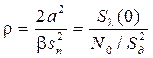 .
.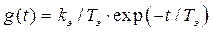 . (7.34)
. (7.34)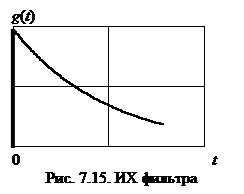 Фильтр с полученными ЧПФ и ИХ можно реализовать с помощью инерционного звена (прил. 2), например интегрирующей RC -цепи, с параметрами kэ и Tэ, которые зависят от ширины спектра воздействия и уровня помехи.
Фильтр с полученными ЧПФ и ИХ можно реализовать с помощью инерционного звена (прил. 2), например интегрирующей RC -цепи, с параметрами kэ и Tэ, которые зависят от ширины спектра воздействия и уровня помехи.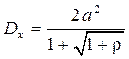 [2].
[2]. На рис. 7.16 показана зависимость параметров синтезированного фильтра kэ и Tэ от соотношения спектральных плотностей воздействия и возмущения (r). Из рисунка видно, что при уменьшении спектральной плотности помехи оптимальный КУ kэ растет, а оптимальная постоянная времени фильтра Tэ уменьшается. Это объясняется тем, что при малой интенсивности помехи основной вклад в СКО вносит составляющая, вызванная искажением процесса l(t) при прохождении его через фильтр. Для ее уменьшения необходимо расширять полосу пропускания и увеличивать КУ. Если преобладает спектральная плотность помехи, то для снижения СКО потребуются обратные действия.
На рис. 7.16 показана зависимость параметров синтезированного фильтра kэ и Tэ от соотношения спектральных плотностей воздействия и возмущения (r). Из рисунка видно, что при уменьшении спектральной плотности помехи оптимальный КУ kэ растет, а оптимальная постоянная времени фильтра Tэ уменьшается. Это объясняется тем, что при малой интенсивности помехи основной вклад в СКО вносит составляющая, вызванная искажением процесса l(t) при прохождении его через фильтр. Для ее уменьшения необходимо расширять полосу пропускания и увеличивать КУ. Если преобладает спектральная плотность помехи, то для снижения СКО потребуются обратные действия.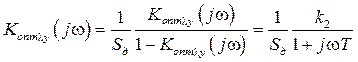 , (7.35)
, (7.35)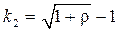 ,
, 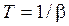 .
. Если входное воздействие и помеха являются нестационарными случайными процессами, то фильтр будет также нестационарным.
Если входное воздействие и помеха являются нестационарными случайными процессами, то фильтр будет также нестационарным.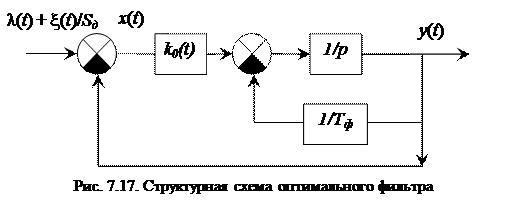
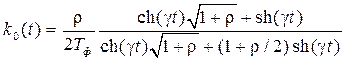 ,
,  . (7.36)
. (7.36)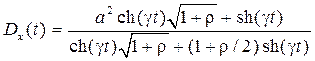 . (7.37)
. (7.37)





