Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Анализ качества работы дискретных системСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Устойчивость дискретных следящих систем связана с расположением полюсов ее ПФ на комплексной плоскости. Как было отмечено ранее (гл. 4), непрерывная РАС будет устойчива, если полюсы ее ПФ находятся в левой комплексной полуплоскости. Учитывая связь Z -преобразования и ЧПФ РАС, получаем, что левая комплексная полуплоскость в результате преобразуется в круг единичного радиуса на плоскости переменной z. Отсюда следует, что дискретная система будет устойчива, если полюсы zi её ПФ K (z) находятся внутри окружности единичного радиуса на плоскости переменной z, а значит, удовлетворяют условию: | zi | < 1. Полюсы ПФ zi являются корнями характеристического уравнения При переходе к псевдочастоте Кроме прямого вычисления корней характеристического уравнения, как и у непрерывных РАС используют алгебраические (для ПФ порядка не превышающего 5) и частотные критерии. Например, алгебраический критерий устойчивости требует, чтобы коэффициенты характеристического уравнения устойчивой дискретной системы удовлетворяли определенной системе неравенств. Условие устойчивости для уравнения первого порядка (n = 1): а1 + а0 > 0, a1 – a0 > 0. (9.13) Условие устойчивости для уравнения второго порядка (n = 2): a2 + a1 + a0 > 0, a2 – a1 + a0 > 0, a2 – a0 > 0. (9.14) Для характеристических уравнений более высоких порядков формулы алгебраического критерия устойчивости можно найти в [2, 18]. Критерий устойчивости Найквиста требует, чтобы годограф комплексной ЧПФ разомкнутой дискретной РАС (W (z) = W (p) при подстановке z = exp(i w T)) не охватывал критическую точку (–1, i 0) на плоскости комплексной переменной ω, при этом достаточно изменять ω в пределах от 0 до Пример 9.3. Проанализируем устойчивость дискретной РАС из примера 9.2 (рис. 9.2) с приведенной ПФ Из (9.12) следует, что При линеаризованном дискриминаторе с крутизной характеристики Sд получаем такую ПФ по ошибке:
Характеристическое уравнение в этом случае имеет вид (n = 1):
Из (9.11) следует, что a1 = 1; a0 =
Первое условие всегда выполняется при нахождении величины рассогласования на линейном (рабочем) участке характеристики (Sд > 0). Выполнение второго условия накладывает ограничения на допустимую величину периода дискретизации Тд и коэффициента передачи по контуру регулирования Sдkи . В то же время непрерывная РАС с одним интегратором устойчива при любой глубине обратной связи. Причина неустойчивости РАС при невыполнении второго условия заключается в прерывистом характере регулирования, при котором напряжения на выходе интегратора определяется не текущим значением ошибки, а ее значением в дискретные моменты времени t = nТд [2]. Аналогичные выводы получаются и по другим критериям. Например, в этом случае после получения формулы (9.15) проще всего было проанализировать полюсы (нули знаменателя) (9.15) на выполнение условия | zi | < 1. В данном случае получаем:
Анализ детерминированных процессов в дискретных РАС c помощью Z -преобразования проводится аналогично применению операторного метода при анализе непрерывных РАС. Сначала необходимо получить Z -преобразования ПФ K (z) и входного процесса Λ(z). Тогда анализируемый выходной процесс определяется перемножением их Z -преобразований: Y (z) = K λ y (z)Λ(z) или X (z) = K λ x (z)Λ(z). (9.17) По полученному Z -преобразования выходного процесса (Y (z) или X (z)) отыскиваются значения отчетов (дискретов) во временной области (y (nТд) или x (nТд)). Существует несколько способов обращения Z -преобразования. Напрямую интеграл обращения вычисляется с использованием теорема о вычетах:
где zi – полюсы подынтегральной функции f (z)= Y (z) z n –1 [2, 18]. В общем случае вычет в полюсе m -го порядка определяется так:
а в случае простого полюса:
Однако на практике обычно предпочитают пользоваться таблицами Z -преобразования [2, 5, 18]. Для этого необходимо представить Y (z) или X (z) в виде составляющих, имеющих известное (табличное – см. прил. 1) Z -преобразование.
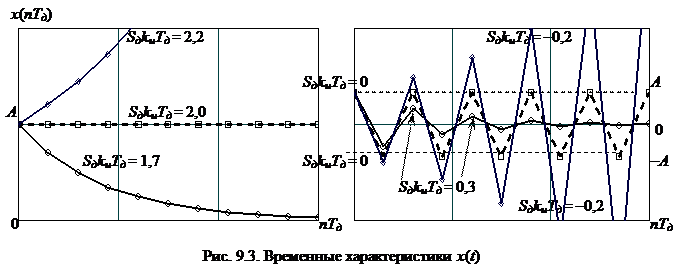
Пример 9.4. Определим ошибку слежения x (t) в дискретной РАС из примера 9.2 при воздействии λ(t) = A 1(t) и возмущении ξ(t) = 0. По таблице из прил. 1 определяем Подставляя результаты примера 9.3, получаем
Установившееся значение ошибки определяем по теореме о конечном значении оригинала (9.8):
Для определения ошибки в переходном режиме используем теорему о вычетах (9.20). Так как ПФ имеет один простой полюс (
В данном примере прямое вычисление по теореме вычетов оказывается проще, чем использование таблицы из прил. 1.
На рис. 9.3 приведены графики x (t) при различных значениях SдkиТд.
|
||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 1081; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.242.39 (0.007 с.) |

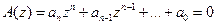 , которое получается приравниванием нулю знаменателя ПФ K (z).
, которое получается приравниванием нулю знаменателя ПФ K (z).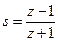 можно получить ПФ K (s), которая имеет то же поведение, что и K (p), что позволяет использовать любые методы анализа устойчивости, приведенные в гл. 4, относительно новой переменной s [18].
можно получить ПФ K (s), которая имеет то же поведение, что и K (p), что позволяет использовать любые методы анализа устойчивости, приведенные в гл. 4, относительно новой переменной s [18].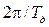 [2].
[2].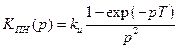 .
.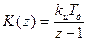 .
.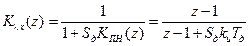 . (9.15)
. (9.15)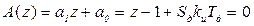 .
.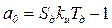 и условия устойчивости будут иметь вид:
и условия устойчивости будут иметь вид: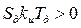 ;
; 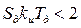 . (9.16)
. (9.16)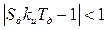 , что после снятия знака модуля приводит к полученным ранее условиям (9.16).
, что после снятия знака модуля приводит к полученным ранее условиям (9.16). , (9.18)
, (9.18)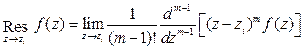 , (9.19)
, (9.19)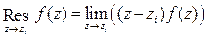 . (9.20)
. (9.20)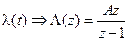 .
. .
.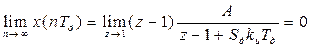 .
.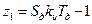 ), то
), то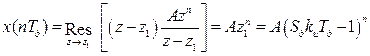 . (9.21)
. (9.21)