
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Цифровые системы радиоавтоматикиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте В современных радиотехнических устройствах и системах широко применяются цифровые РАС, в состав которых входят вычислительные или специализированные цифровые устройства. Быстрое внедрение в технику цифровых систем произошло в 90-е годы ХХ века. В эти годы начался штурм скоростей работы вычислителей, объемов доступной памяти и т. п., что привело к качественным скачкам технологий и широкому внедрению цифровых устройств и методов обработки сигналов в радиотехнику, электросвязь и радиосвязь. В цифровых системах, выполненных на базе микроэлектроники, при небольших габаритах и массах вычислительных устройств можно использовать сложные алгоритмы обработки сигналов, при этом точность реализации алгоритмов может быть сделана весьма высокой по сравнению с аналоговыми. Важным преимуществом цифровых систем является высокая стабильность их работы. В таких РАС отсутствует дрейф нуля дискриминаторов, усилителей и других узлов системы. В цифровых РАС легко осуществляется перестройка структуры и изменение параметров. Например, если в аналоговой РАС потребуется заменить в процессе работы ФНЧ на полосовой фильтр или ПИФ, а также изменить порядок фильтра, то для реализации этих действий потребуется изменить схему за счет коммутирующих элементов. В цифровых же фильтрах в этом случае изменений в схеме не потребуется, а необходимые корректирующие действия будут реализованы программно. Очевидно, что в последнем случае будет получено малое время перестройки РАС на новый режим работы, а также может быть реализовано весьма гибкое регулирование.
На рис. 9.5 приведена структурная схема цифровой РАС, близкой к рассмотренным ранее аналоговым, в которой цифровой вычислитель (ЦФ) выполняет только функцию корректирующего фильтра. В этой РАС используется аналоговые дискриминатор (Д) и управляемый генератор (ГУН). Для перехода от аналогового сигнала к цифровому необходим аналогово-цифровой преобразователь (АЦП), а для обратного перехода к аналоговому сигналу – цифро-аналоговый преобразователь (ЦАП). Связь между цифровой и аналоговой частью как раз осуществляется с помощью АЦП и ЦАП. В настоящее время возможно построение РАС полностью из цифровых элементов. На рис. 9.6 приведена схема полностью цифровой РАС (цифровой системы ФАПЧ) – все элементы системы: (фазовый дискриминатор (ЦФД), вычислитель (фильтр) (ЦФ), регулятор (ЦР), управляемый генератор (ЦГ), – являются цифровыми. На один вход ЦФД такой системы поступает периодический сигнал, форма которого с помощью формирующего устройства преобразуется в импульсы. В ЦФД вырабатывается кодовая последовательность, соответствующая разности фаз входного сигнала (например, эталонного генератора) и управляемого ЦГ, импульсная последовательность с которого поступает на второй вход ЦФД. Сигнал с выхода ЦФД обрабатывается по определенному алгоритму в вычислителе (ЦФ), а затем подается на цифровой регулятор (ЦР), сигнал которого определяет частоту импульсов ЦГ.
На рис. 9.7 приведена аналогово-цифровая РАС, в которой на вычислитель (цифровой фильтр – ЦФ), кроме функции фильтра, возложены также и функции элемента сравнения (дискриминатора). В этом случае сравнение сигналов осуществляется цифровыми методами и сразу же осуществляется цифровая обработка сигнала ошибки.
Строгая формулировка теорем Котельникова и Найквиста, а также важные частные случаи, разбираются в дисциплинах, связанных с цифровой обработкой сигналов. На рис. 9.8а показан непрерывный сигнал U (t) на входе дискретизатора, а на рис. 9.8б – d-функции, повторяющиеся через период дискретизации Тд. «Фильтрующее» свойство d-функции (штриховые линии на рис. 9.8а) в результате перемножения функций U (t)d(t – nТд) и дальнейшей обработки оставляет от непрерывного сигнала U (t) только его отсчеты U (nТд) (рис. 9.8в), отстоящие друг от друга по оси времени на величину, равную периоду дискретизации Тд. Отметим, что чем больше частота дискретизации, по сравнению с граничным значением по теореме Котельникова (9.25), тем более простой фильтр потребуется для восстановления сигнала обратно в непрерывную форму. Возможности цифрового вычислителя (требуемая скорость вычислений) ограничивают допустимую частоту дискретизации сверху. После дискретизации для перевода в цифровую форму сигнал необходимо квантовать по уровню. В результате аналогово-цифрового преобразования напряжению отсчетов U (nТд) будет поставлен в соответствие число (цифровой код), значение которого пропорционально U (nТд).
Если АЦП имеет n разрядов, то число уровней квантования составляет 2 n – 1. На рис. 9.9 приведена типичная характеристика квантователя. На выходе АЦП получаются числа (цифровой код), которые следуют с частотой дискретизации (fд = 1/ Тд). Квантование сигналов по уровню является в общем случае нелинейной операцией, однако при большом числе уровней квантования (n > 8), что характерно для современных РАС, характеристику преобразования можно приближенно считать линейной, а допускаемую при квантовании погрешность в этом случае допустимо учитывать как шум квантования. Шум квантования в обычных случаях представляется как белый шум с математическим ожиданием mx = 0 и дисперсией Dx = q2 /12 [1, 2]. Чем меньше шаг квантования (больше число уровней квантования или больше разрядность выходного кода) при заданном максимальном уровне входного сигнала, тем меньше допускаемая погрешность, а значит, и шум квантования. Входные и выходные сигналы цифровых систем являются последовательностями, которые связываются разностными уравнениями, однако при анализе удобно взять за основу алгоритм вычислителя, в соответствии с которым входные сигналы преобразуются в выходные. В этом случае вычислитель РАС можно представить как последовательное соединение цифрового фильтра, в котором осуществляется преобразование сигналов, и звена запаздывания, которое учитывает время прохождения сигнала через цифровой фильтр. Время запаздывания зависит от сложности выполняемого алгоритма и быстродействия вычислителя. Кроме ошибок квантования, в цифровых системах необходимо учитывать также ошибки округления (усечения) результатов арифметических операций и ошибки округления (усечения) коэффициентов цифровой фильтрации при их реализации. Основное влияние на точность вычислений оказывает округление результатов умножения. Если при сложении двух чисел разрядности n для точного представления суммы в накопителе результата («аккумуляторе») потребуется n +1 разрядов, то при их же умножении – 2 n. Так как при реализации сложных алгоритмов количество операций вычислителя значительно, для точного представления результата требуется очень большая разрядность «аккумулятора», что обычно оказывается не допустимым в реализации. Ограниченная разрядность «аккумулятора» и приводит к необходимости округления результатов вычислений. В большинстве случаев это не приводит к значимым погрешностям, но в некоторых случаях может привести к большим ошибкам. Рассмотрим пример: к очень большому числу N прибавляется очень маленькое k, а затем то же большое число N вычитается. В результате может получиться ноль или число, меньшее k, так как при округлении суммы (N + k) маленькое число k может существенно потерять точность представления или даже совсем исчезнуть. Если в алгоритме на это число ((N + k) – N) в последующем выполняется деление, то появляется большая погрешность. Рассмотренные проблемы следует учитывать при оценке и выборе длины накопителя результатов вычислений («аккумулятора»). Округление коэффициентов фильтрации приводит к смещению полюсов ПФ, что в некоторых случаях может оказаться существенным. Анализ устойчивости и определение показателей качества работы цифровых РАС проводится теми же методами, что и в рассмотренных ранее дискретных РАС. Синтез цифровых РАС сводится к выбору цифрового корректирующего устройства, последовательное включение которого с объектом управления позволяет получить заданные характеристики регулирования.
Пример 9.6. Найти ПФ WК(z) цифрового корректирующего устройства РАС из примера 9.2 (рис. 9.2), ПФ разомкнутой системы которой W(p) = Пусть желаемая ПФ аналогового эквивалента [1] Wa (p) = 1/(1 + pT1)/(1 + pT2). После Z -преобразования желаемой ПФ проектируемой системы получаем по формулам из таблицы прил. 1:
Так как кроме корректирующего ЦФ в ПФ разомкнутой РАС содержится еще и объект управления (рис. 9.2) интегрирующего типа (
Анализ показывает [1], что значения переходных характеристик (ПХ) в цифровой РАС и ее аналоговом эквиваленте в установившемся режиме несколько различаются. Однако с уменьшением периода Тд в цифровой РАС расхождение между дискретными значениями ПХ и ПХ непрерывного эквивалента (ПХ h (t) в моменты времени t = nТд) уменьшается, и при Тд ® 0 значения ПХ в точках t = nТд совпадают [1]. Обычно желательно обеспечить, чтобы переходные процессы в цифровой РАС завершались за один такт работы. После определения ПФ корректирующего устройства следующим этапом синтеза цифровой РАС является его техническая реализация. ПФ рекурсивного цифрового фильтра удобно записать в виде (9.6)
(Рекурсивный ЦФ использует в вычислениях текущего значения выходного процесса y [ n ] предшествующие значения не только входного x [ n – 1 ], x [ n – 2 ],..., но и выходного процесса y [ n – 1 ], y [ n – 2 ],...)
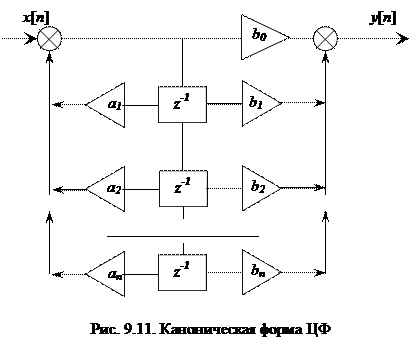
Такую форму представления ПФ удобно реализовать в так называемой прямой форме представления ЦФ. На рис. 9.10 представлена структурная схема ЦФ прямой формы. Каждое звено z-1 соответствует задержке сигнала на один такт, и в цифровой форме реализуется в виде запоминающего устройства сдвигового типа. Недостатком реализации ЦФ в прямой форме является большое количество (2 n) необходимых линий задержки.
Сократить это количество в 2 раза позволяет каноническая форма реализации ЦФ, представленная на рис. 9.11. В этом случае коэффициенты фильтра an и bn из (9.26) потребуют перерасчета. Следует отметить, что современные ЦФ обычно реализуются в программной форме с использованием микропроцессоров и т. п. Список рекомендуемой литературы: [ 1, с. 152-178, 181-192, 195-203, 208-215; 2, с. 202-225, 231-255; 3, с. 430-472, 693-708; 4, с. 164-223; 5, с. 196-202, 213-246; 6, с. 120-123; 9, с. 12-15, 36-41, 67-69, 74-76, 86-89, 229-242, 289-296, 427-432; 10, т. 2, с. 73-75; 11, с. 543-586; 13, с. 492-498; 16; 18, с. 138-185; 20, 21, 26; 27, с. 386-398]. Контрольные вопросы 1. Укажите преимущества и недостатки дискретных РАС по сравнению с аналоговыми и цифровыми РАС. 2. Назовите методы математического описания дискретных РАС. 3. Что такое Z-преобразование, и как его используют в анализе дискретных РАС? 4. Опишите последовательность получения ПФ замкнутой дискретной РАС. 5. Приведите примеры дискретных РАС и дайте характеристику их особенностей. 6. Приведите примеры элементов дискретных РАС и опишите их особенности. 7. Опишите особенности анализа устойчивости дискретных РАС. 8. Как оценивают ошибку слежения в установившемся режиме в дискретной РАС? 9. Опишите последовательность анализа смешанных воздействий на дискретную РАС. 10. Как оценивается астатизм дискретных РАС? 11. Как влияет астатизм дискретных РАС на ошибку в установившемся режиме? 12. Какие преимущества и недостатки имеют цифровые РАС по сравнению с аналоговыми и дискретными РАС? 13. Укажите методы математического описания цифровых РАС. 14. Какие особенности имеют программные и аппаратные реализации цифровых фильтров цифровых РАС? 15. Опишите последовательность синтеза цифрового фильтра с помощью метода билинейного преобразования. 16. Приведите примеры цифровых РАС и дайте характеристику их особенностей. 17. Приведите примеры элементов цифровых РАС и опишите их особенности. 18. Опишите цифровую систему ФАПЧ. 19. Что такое погрешности квантования и округления, и как они влияют на характеристики цифровых РАС?
Примеры применения систем ФАПЧ В радиотехнике Рассмотрим примеры применения системы ФАПЧ в радиотехнических устройствах. Цифровая система ФАПЧ Цифровые системы ФАПЧ широко используются в синтезаторах частоты. Применение цифровых делителей частоты внутри петли регулирования ФАПЧ позволяет простыми средствами получить необходимую сетку частот. На рис. 10.1 приведена структурная схема системы цифровой ФАПЧ, которая используется в лабораторном стенде [6]. Данный стенд позволяет пользователю, задавая с помощью клавиатуры коэффициент деления и опорную частоту, получать функциональные сигналы («меандр, «пила», «синусоида» и т. п.) различных частот на выходе стенда. Кроме того, на другом выходе стенда возможно наблюдение сигналов с контрольных точек, которые также выбираются с помощью клавиатуры. На одном входе рассматриваемой схемы ФД поставлен делитель частоты на N. Петля ФАПЧ в результате регулирования будет добиваться совпадения частоты эталонного генератора и частоты ГУН, деленной на N. Если бы частоту эталонного генератора перед подачей на второй вход ФД также подвергали бы делению на M, то выполнялось бы следующее условие:
Формула (10.1) используется при формировании сетки частот.
В схеме, представленной на рис. 10.1, опорная частота формируется программно, и такое деление на M не используется (M = 1). На рис. 10.2 показана петля ФАПЧ с описанными выше делителями частоты, которая используется при формировании сетки частот.
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 1193; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.01 с.) |



 На рис. 9.8 показана процедура дискретизации аналогового сигнала. Выбор частоты дискретизации осуществляется на основании теоремы Котельникова: частота дискретизации fд должна в общем случае быть как минимум в два раза больше, чем верхняя частота спектра сигнала fв :
На рис. 9.8 показана процедура дискретизации аналогового сигнала. Выбор частоты дискретизации осуществляется на основании теоремы Котельникова: частота дискретизации fд должна в общем случае быть как минимум в два раза больше, чем верхняя частота спектра сигнала fв :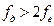 . (9.25)
. (9.25) В результате квантования из всех возможных значений дискретных сигналов выбираются только определенные разрешенные уровни, кратные шагу квантования q, равного значению младшего разряда АЦП.
В результате квантования из всех возможных значений дискретных сигналов выбираются только определенные разрешенные уровни, кратные шагу квантования q, равного значению младшего разряда АЦП.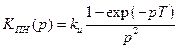 .
. .
. ) с Z -преобразованием
) с Z -преобразованием  , можно определить Z -преобразование WК(z):
, можно определить Z -преобразование WК(z): .
. . (9.26)
. (9.26)
 . (10.1)
. (10.1)




