Тема 12. Аналого-цифровые преобразователи

 

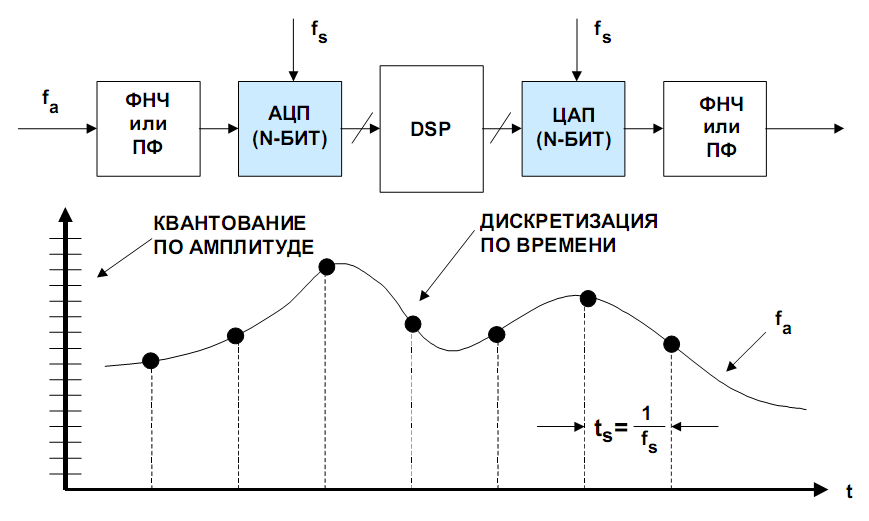
Блок-схема типичной цифровой системы представлена на рисунке 12.1. Обычно, прежде чем подвергнуться реальному аналого-цифровому преобразованию, аналоговый сигнал проходит через цепи нормализации, которые выполняют такие функции, как усиление (или ослабление) и фильтрация. Для подавления нежелательных сигналов вне полосы пропускания и предотвращения наложения спектров необходим фильтр низкой частоты или полосовой фильтр.

 

 

Рисунок 12.1 – Структура цифровой системы

 

На рис. 12.1 представлена система, работающая в реальном масштабе времени. В ней АЦП непрерывно дискретизирует сигнал с частотой, равной fs, и выдает новый отсчет процессору ЦОС (DSP) с такой же частотой. Для обеспечения работы в реальном масштабе времени DSP должен закончить все вычисления в пределах интервала дискретизации 1/fs и передать выходной отсчет на ЦАП до поступления следующего отсчета с АЦП.

Нужно отметить, что ЦАП требуется только в том случае, когда данные необходимо преобразовать обратно в аналоговый сигнал (например, в случае звукового приложения). Во многих приложениях после первоначального аналого-цифрового преобразования сигнал остается в цифровом формате. Кроме того, существуют устройства подобные CD-проигрывателю, в которых DSP отвечает исключительно за формирование сигнала на ЦАП. В случае использования ЦАП, на его выходе для подавления нежелательных гармоник необходимо применять фильтр.

В реальных процессах аналого-цифрового и цифро-аналогового преобразования есть два ключевых этапа: дискретизация по времени и квантование по амплитуде, которые определяют разрешающую способность данных операций.

Разрешающая способность преобразователей данных может быть выражена несколькими различными способами: весом младшего разряда (LSB), долей от полной шкалы размером в один миллион (ppm FS), милливольтами (мВ) и т.д.

Величина младшего значащего разряда (LSB) для приборов с различной разрешающей способностью при диапазоне шкалы квантования в 10 В приведена таблице 12.1.

 

Таблица 12.1 – Величины, соответствующие младшему биту (LSB) квантования (вся шкала (FS) – 10 В)

 

Статическая передаточная функция АЦП И ЦАП и погрешности по постоянному току.

Наиболее общей характеристикой, описывающей свойства аналого-цифрового и цифро-аналогового преобразования, являются статическая передаточная характеристика АЦП и ЦАП. Они имеют одинаковые параметры погрешностей, поэтому ниже рассматриваются совместно.

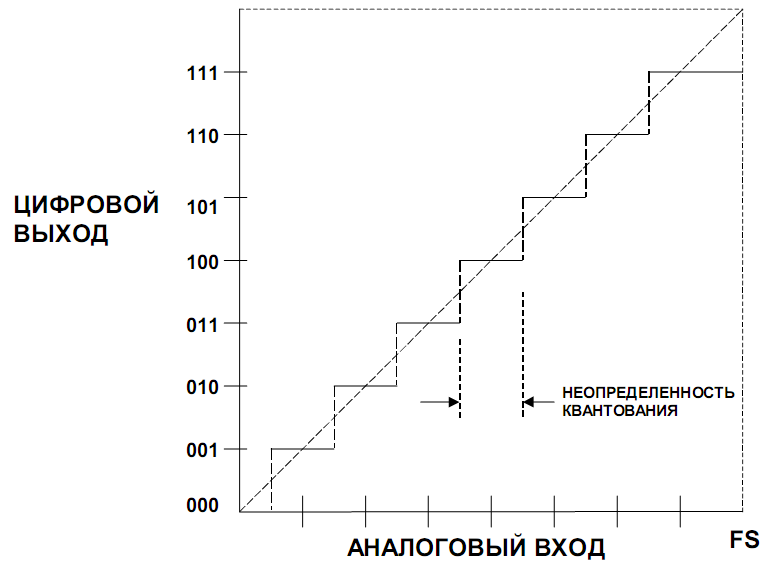
Первые преобразователи данных применялись в области измерения и управления, где точный выбор времени преобразования обычно не имел значения, и скорость передачи данных была невелика. В таких приложениях были важны характеристики АЦП и ЦАП по постоянному току, а характеристики, связанные с синхронизацией и характеристики по переменному току не имели существенного значения. Однако сегодня ко многим, если не к большинству преобразователей, используемых в системах дискретизации и восстановления сигнала, предъявляются жесткие требования по характеристикам на переменном токе (характеристики по постоянному току могут быть не существенны). Данные характеристики будут рассмотрены далее.

На рис. 12.2 представлена идеальная функция передачи однополярного 3-разрядного АЦП, а на рис. 12.3 –3-разрядного ЦАП.

 

 

Рисунок. 12.2 – Статическая передаточная характеристика идеального однополярного 3-разрядного АЦП

 

 

Рисунок. 12.3 – Статическая передаточная характеристика идеального 3-разрядного ЦАП

Входной аналоговый сигнал АЦП не квантован, но его выходной сигнал является результатом квантования. Поэтому характеристика передачи состоит из восьми горизонтальных прямых (при рассмотрении смещения, усиления и линейности АЦП рассматривается линия, соединяющая средние точки этих отрезков).

В ЦАП входной и выходной сигналы квантованы, и график содержит восемь точек. Независимо от способа аппроксимации этой функции, важно помнить, что реальной характеристикой передачи является не линия, а множество дискретных точек.

В обоих случаях полная цифровая шкала (все "1") соответствует полной аналоговой шкале минус значение младшего разряда LSB (значение, формируемое источником опорного напряжения или кратная ему величина). Это происходит потому, что цифровой код представляет собой нормализованное отношение аналогового сигнала к опорному сигналу.

Переходы АЦП (идеальные) имеют место, начиная с ½ LSB выше нуля, и далее через каждый LSB, до 1½ LSB ниже полной аналоговой шкалы. Так как входной аналоговый сигнал АЦП может иметь любое значение, а выходной цифровой сигнал квантуется, может существовать различие до ½ LSB между реальным входным аналоговым сигналом и точным значением выходного цифрового сигнала. Этот эффект известен как ошибка (погрешность) или неопределенность квантования и проиллюстрирован на рис. 12.2. В приложениях, использующих сигналы переменного тока, эта ошибка квантования вызывает явление, называемое шумом квантования.

В примерах на рис. 12.2 и 12.3 применяются униполярные преобразователи, работающие с сигналом только одной полярности. Это самый простой тип, но в реальных приложениях более полезны биполярные преобразователи. Имеется два типа биполярных преобразователей. Более простой из них – это в сущности просто униполярный преобразователь с отрицательным смещением на величину, соответствующую единице старшего разряда (MSB), (во многих преобразователях можно переключать это смещение, чтобы использовать их и как униполярные, и как биполярные). Другой, более сложный тип, известен как преобразователь знака (sign-magnitude) и имеет N информационных разрядов, а также дополнительный разряд, который показывает знак аналогового сигнала. ЦАП этого типа применяется довольно редко, а на таких АЦП типа сконструированы большинство цифровых вольтметров.

В АЦП и ЦАП различают четыре типа погрешностей по постоянному току: погрешность смещения, погрешность усиления и два типа погрешностей, связанных с линейностью.

Погрешности смещения и усиления АЦП и ЦАП аналогичны погрешностям смещения и усиления в усилителях. На рис. 12.4 показано преобразование входных сигналов биполярного диапазона (хотя погрешность смещения и погрешность нуля, идентичные в усилителях и униполярных АЦП и ЦАП, различны в биполярных преобразователях, и это следует учитывать).

 

Рисунок 12.4 – Погрешность смещения нуля преобразователя и погрешность усиления

 

Характеристики передачи и ЦАП, и АЦП могут быть выражены как D=K+GA, где D – цифровой код, А – аналоговый сигнал, K и G – константы. В униполярном преобразователе K равно 0, в биполярном преобразователе со смещением – 1 MSB. Погрешность смещения – это величина, на которую фактическое значение K отличается от идеального значения. Погрешность усиления – это величина, на которую G отличается от идеального значения. В общем случае, погрешность усиления может быть выражена разностью двух коэффициентов, выраженной в процентах. Эту разность можно рассматривать, как вклад погрешности усиления (в мВ или значениях младшего разряда) в общую погрешность при максимальном значении сигнала. Обычно пользователю предоставляется возможность минимизации этих погрешностей. В случае операционного усилителя сначала регулируют смещение усилителя при нулевом входном сигнале, а затем настраивают коэффициент усиления при значении входного сигнала, близких к максимальному. Алгоритм настройки биполярных преобразователей более сложен.

Интегральная нелинейность ЦАП и АЦП аналогична нелинейности усилителя и определяется как максимальное отклонение фактической характеристики передачи преобразователя от прямой линии. В общем случае, она выражается в процентах от полной шкалы (но может представляться в значениях младших разрядов). Существует два общих метода аппроксимации характеристики передачи: метод конечных точек (end point) и метод наилучшей прямой (best straight line) (рис. 12.5).

 

 

Рисунок 12.5 – Методы измерения суммарной погрешности линейности

 

При использовании метода конечных точек измеряется отклонение произвольной точки характеристики (после коррекции усиления) от прямой, проведенной из начала координат.

Метод наилучшей прямой дает более адекватный прогноз искажений в приложениях, имеющих дело с сигналами переменного тока. Он менее чувствителен к нелинейностям технических характеристик. По методу наилучшего приближения через характеристику передачи устройства проводят прямую линию, используя стандартные методы интерполяции кривой. После этого максимальное отклонение измеряется от построенной прямой. Как правило, интегральная нелинейность, измеренная таким образом, учитывает только 50% нелинейности, оцененной методом конечных точек. Это делает метод предпочтительным при указании впечатляющих технических характеристик в спецификации, но менее полезным для анализа реальных значений погрешностей. Для приложений, имеющих дело с сигналами переменного тока, лучше определять гармонические искажения, чем нелинейность по постоянному току, так что для определения нелинейности преобразователя необходимость в использовании метода наилучшей прямой возникает довольно редко.

Другой тип нелинейности преобразователей – дифференциальная нелинейность (DNL). Она связана с нелинейностью кодовых переходов преобразователя. В идеальном случае изменение на единицу младшего разряда цифрового кода точно соответствует изменению аналогового сигнала на величину единицы младшего разряда. В ЦАП изменение одного младшего разряда цифрового кода должно вызывать изменение сигнала на аналоговом выходе, в точности соответствующее величине младшего разряда. В то же время в АЦП при переходе с одного цифрового уровня на следующий значение сигнала на аналоговом входе должно измениться точно на величину, соответствующую младшему разряду цифровой шкалы.

Там, где изменение аналогового сигнала, соответствующее изменению единицы младшего разряда цифрового кода, больше или меньше этой величины, говорят об дифференциальной нелинейной (DNL) погрешности. DNL-погрешность преобразователя обычно определяется как максимальное значение дифференциальной нелинейности, выявляемое на любом переходе.

Если дифференциальная нелинейность ЦАП меньше, чем –1 LSB на любом переходе (рис. 12.6), ЦАП называют немонотонным, и его характеристика передачи содержит один или несколько локальных максимумов или минимумов. Дифференциальная нелинейность, большая чем +1 LSB, не вызывает нарушения монотонности, но также нежелательна. Во многих приложениях ЦАП (особенно в системах с обратной связью, где немонотонность может изменить отрицательную обратную связь на положительную) монотонность ЦАП очень важна. Часто монотонность ЦАП явно оговаривается в техническом описании, хотя, если дифференциальная нелинейность гарантированно меньше единицы младшего разряда (то есть, |DNL| ≤ 1LSB), устройство будет обладать монотонностью, даже если это явно не указывается.

 

 

Рисунок 12.6 – Статическая передаточная характеристика неидеального 3-разрядного ЦАП

 

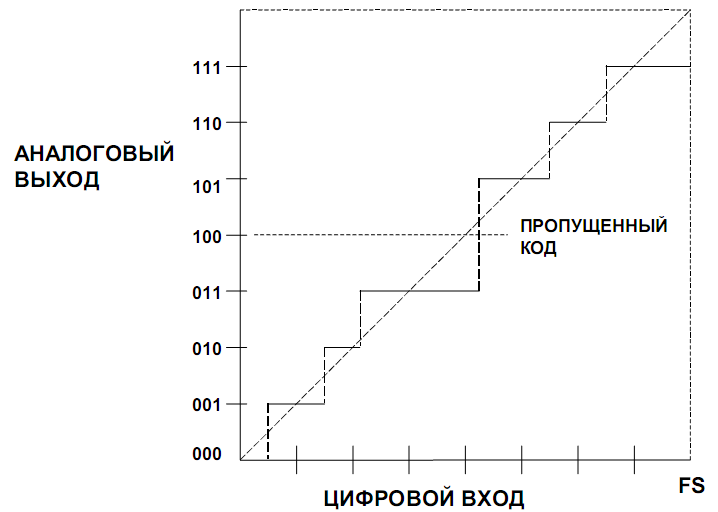
Бывает, что АЦП немонотонен, но наиболее распространенным проявлением DNL в АЦП являются пропущенные коды (рис. 12.7). Пропущенные коды (или немонотонность) в АЦП столь же нежелательны, как немонотонность в ЦАП. Опять таки, это возникает при DNL > 1 LSB.

 

 

Рисунок 12.7 – Статическая передаточная характеристика неидеального 3-разрядного АЦП

 

Определение отсутствующих кодов сложнее, чем определение немонотонности. Все АЦП характеризуются некоторым шумом перехода (transition noise), иллюстрируемым на рис. 12.8 (представьте себе этот шум как мелькание последней цифры цифрового вольтметра между соседними значениями). По мере роста разрешающей способности диапазон входного сигнала, соответствующий уровню шума перехода, может достичь или даже превысить значение сигнала, соответствующее единице младшего разряда. В таком случае, особенно в сочетании с отрицательной DNL- погрешностью, может случиться так, что появятся некоторые (или даже все) коды, где шум перехода будет присутствовать во всем диапазоне значений входных сигналов. Таким образом, возможно существование некоторых кодов, для которых не существует значения входного сигнала, при котором этот код гарантированно бы появился на выходе, хотя и может существовать некоторый диапазон входного сигнала, при котором иногда будет появляться этот код.

 

 

Рисунок 12.8 – Совместное действие шума перехода кода АЦП и дифференциальной нелинейности (DNL)

 

Динамические параметры (погрешности по переменному току) АЦП

Если параметры по постоянному току можно рассматривать одновременно и для ЦАП, и для АЦП, то их характеристики по переменному току слишком различаются.

Искажения и шум в идеальном N-разрядном АЦП

Анализ передаточной характеристики АЦП проводился без рассмотрения такой операции, как квантование. Теперь будем трактовать АЦП как идеальный дискретизатор, но учитывать при этом эффекты квантования.

Идеальный N-разрядный АЦП имеет погрешности (по постоянному или переменному току), связанные только с процессами дискретизации и квантования. Максимальная погрешность, которую имеет идеальный АЦП при оцифровывании входного сигнала, равна ±1/2 LSB. Любой аналоговый сигнал, поступающий на вход идеального N-разрядного АЦП, производит шум квантования. Среднеквадратичное значение шума (измеренное по ширине полосы Найквиста, от постоянного тока до fs/2) приблизительно равно весу наименьшего значащего разряда q, деленному на √12. При этом предполагается, что амплитуда сигнала составляет, по крайней мере, несколько младших разрядов, так что выход АЦП изменяет свое состояние почти при каждом отсчете. Сигнал ошибки квантования от входного линейного пилообразного сигнала аппроксимируется сигналом пилообразной формы с максимальным размахом q, и его среднеквадратичное значение равно q/√12 (рис. 12.9).

Отношение среднеквадратичного значения синусоидального сигнала, соответствующего полной шкале, к среднеквадратичному значению шума квантования (выраженное в дБ) равно:

 

ОСШ = 6,02N + 1,76 дБ, (12.1)

 

где N - число разрядов в идеальном АЦП.

Это уравнение имеет силу только в том случае, если шум измерен на полной ширине полосы Найквиста от 0 до fs /2. Если ширина полосы сигнала BW меньше fs /2, то значение отношения сигнал/шум (SNR) в пределах ширины полосы сигнала BW возрастет вследствие уменьшения энергии шума квантования в пределах ширины полосы. Для этого условия правильным будет следующее выражение:

 

(12.2)

 

 

Рисунок 12.9 – Шум квантования идеального N-разрядного АЦП

 

Приведенное уравнение отражает состояние, именуемое избыточной дискретизацией, при котором частота дискретизации выше, чем удвоенная ширина полосы сигнала. Корректирующую величину часто называют запасом по дискретизации. Обратите внимание, что для данной ширины полосы сигнала удвоенная частота дискретизации увеличивает отношение сигнал/шум на 3 дБ.

Хотя среднеквадратичное значение шума довольно точно приближается к q/√12, его частотная область может сильно коррелировать с входным аналоговым сигналом. Например, корреляция будет больше для периодического сигнала малой амплитуды, чем для случайного сигнала большой амплитуды. Весьма часто в теории полагают, что шум квантования появляется в виде белого шума, распределенного равномерно по всей ширине полосы Найквиста от 0 до fs /2. К сожалению, это не так. В случае сильной корреляции шум квантования будет сконцентрирован около каких угодно гармоник входного сигнала.

 

Искажение и шум в реальных АЦП

На практике дискретизация сигнала в АЦП (с интегрированным устройством выборки-хранения УВХ), независимо от архитектуры, проходит при наличии шумов и искажений сигнала, как это показано на рис. 12.10. Широкополосному аналоговому входному буферу присущи широкополосный шум, нелинейность и конечная ширина полосы. УВХ вносит дальнейшую нелинейность, ограничение полосы и дрожание апертуры. Квантующая часть АЦП вносит шум квантования, интегральную и дифференциальную нелинейности.

 

 

Рис. 12.10 – Модель АЦП, показывающая источники шумов и искажений сигнала

 

Приведенный ко входу тепловой шум

Широкополосные внутренние цепи АЦП вносят некоторое среднеквадратичное значение широкополосного шума из-за воздействия тепла и дисперсии шума kT/C. Этот шум присутствует даже для сигналов постоянного тока и объясняет тот факт, что результатом работы большинства широкополосных (с высокой разрешающей способностью) АЦП является распределение кодов, сконцентрированное вокруг номинального значения

входного сигнала. Чтобы измерить его значение, вход АЦП заземляется,

накапливается большое количество выходных отсчетов и составляется график в виде гистограммы (иногда упоминаемый как гистограмма с заземленным входом). Так как шум имеет почти Гауссово распределение, стандартное отклонение гистограммы легко рассчитывается в соответствии с эффективным среднеквадратичным значением входного шума. Обычной практикой для выражения среднеквадратичного значения шума является его выражение в терминах младших разрядов, хотя оно может быть выражено как среднеквадратичное значение напряжения.

Динамические свойства аналогового тракта АЦП характеризуются следующими параметрами:

„ Гармонические искажения

„ Наихудшие гармоники

„ Общие гармонические искажения (THD)

„ Общие гармонические искажения и шум (THD + N)

„ Отношение сигнал-шум и искажения (SINAD, or S/N +D)

„ Эффективное количество разрядов (ENOB)

„ Отношение сигнал-шум (SNR)

„ Аналоговая полоса пропускания (для полного сигнала, для малого сигнала)

„ Динамический диапазон, свободный от гармоник (SFDR)

„ Двухтональные интермодуляционные искажения

„ Многотональные интермодуляционные искажения

 

Явления интегральных и дифференциальных нелинейных искажений

Полная интегральная нелинейность АЦП обусловлена интегральной нелинейностью входного буфера, УВХ и полной интегральной нелинейностью передаточной функции АЦП. Но дифференциальная нелинейность, которая присутствует исключительно вследствие цифрового кодирования, может значительно изменяться в зависимости от принципов применяемого цифрового кодирования АЦП. Полная интегральная нелинейность дает составляющие искажений, у которых амплитуда изменяется в зависимости от амплитуды входного сигнала. В частности, интермодуляционные составляющие второго порядка увеличиваются на 2 дБ при увеличении сигнала на 1 дБ, а составляющие третьего порядка увеличиваются на 3 дБ при повышении уровня сигнала на 1 дБ.

Дифференциальная нелинейность в передаточной функции АЦП порождает гармоники, которые зависят не только от амплитуды сигнала, но и от положения точки дифференциальной нелинейности на передаточной функции АЦП. На рис. 12.11 показаны две передаточные функции АЦП, имеющих различную дифференциальную нелинейность. Левая диаграмма показывает погрешность, которая имеет место при наличии нелинейности в середине шкалы. Поэтому сигнал, проходящий через эту точку, и при "больших", и при "малых" сигналах подвергается искажениям, не зависящим от относительной амплитуды сигнала. Правая диаграмма показывает другую передаточную функцию АЦП, которая имеет погрешности дифференциальной нелинейности в точках, соответствующих 1/4 и 3/4 полной шкалы. Сигналы, превышающие 1/2 шкалы АЦП, подвергнутся действию этих искажений, в то время как сигналы, не превышающие 1/2 шкалы размаха, не имеют искажений.

Большинство быстродействующих АЦП разработаны так, чтобы дифференциальная нелинейность равномерно распределялась по всей ширине динамического диапазона АЦП. Поэтому для сигналов, которые находятся в пределах нескольких дБ полной шкалы АЦП, полная интегральная нелинейность передаточной функции определяет гармонические искажения. Для сигналов более низких уровней содержание гармоник определяется дифференциальной нелинейностью и в общем случае не уменьшается с уменьшением амплитуды сигнала.

 

 

Рисунок 12.11 – Виды дифференциальной нелинейности (DNL) АЦП

 

Нелинейные искажения, наихудшая гармоника, общие нелинейные искажения (THD), общие нелинейные искажения плюс шум (THD + N)

Величина полных нелинейных искажений (THD) определяется как отношение среднеквадратичного значения основной частоты сигнала к среднему значению корня из суммы квадратов его гармоник (существенны только первые пять). Полные нелинейные искажения АЦП также определяются входным сигналом величиной, близкой к полной шкале АЦП, но могут быть найдены и на любом ином уровне.

Полные нелинейные искажения плюс шум (THD + N) являются отношением среднеквадратичного значения основной частоты сигнала к среднему значению корня из суммы квадратов его гармоник и всех шумовых компонент (исключая постоянную составляющую). Ширина полосы, в которой измеряется шум, должна быть задана.

 

Показатель сигнал/шум/искажения (SINAD), показатель сигнал/шум (SNR) и эффективное число разрядов (ENOB)

Сигнал/шум/искажения (SINAD, или S/N+D) – это отношение среднеквадратичного значения амплитуды сигнала к среднему значению корня из суммы квадратов всех других спектральных компонентов, включая гармоники, но исключая постоянную составляющую. SINAD является хорошим индикатором общих динамических характеристик АЦП, таких как функция входной частоты, потому что включает все компоненты, которые создают шум (включая тепловой шум) и искажения. Он часто представляется в виде графика для различных амплитуд входного сигнала. Если ширина полосы сигнала и шума одинаковы, то SINAD = THD+N.

SINAD часто преобразуется в эффективное число разрядов (ENOB), используя выражение для теоретического отношения сигнал/шум (12.1) идеального N-разрядного АЦП. Уравнение решается для N, и значение отношения сигнал/шум заменяется на SINAD:

 

(12.3)

 

Отношение сигнал/шум (SNR или SNR без гармоник) рассчитывается так же, как и SINAD, за исключением того, что из выражения исключаются гармоники сигнала и оставлены только шумовые составляющие. Практически, необходимо исключить только первые пять доминирующих гармоник. Показатель сигнал/шум будет ухудшаться на высоких частотах, но не так быстро как SINAD, так как из него исключены компоненты гармоник.

 

Аналоговая ширина полосы – это та частота, на которой спектральный выход основной смещенной частоты уменьшается на 3 дБ. Она может быть определено как для малого сигнала (полоса пропускания малого сигнала SSBW), так и для сигнала на уровне полной шкалы (полоса пропускания максимального сигнала FPBW). Как и для усилителя, спецификация аналоговой полосы пропускания преобразователя не предполагает, что АЦП поддерживает хорошие характеристики гармонических искажений во всей полосе частот. В действительности, SINAD (или ENOB) большинства АЦП начинает ухудшаться значительно раньше, чем частота входного сигнала приблизится к значению, соответствующему ослаблению на 3 дБ.

 

Динамический диапазон, свободный от гармоник(SFDR)

Наиболее значительным параметром АЦП, используемых в коммуникационных приложениях, является их динамический диапазон, свободный от гармоник (SFDR).

SFDR АЦП определяется как отношение среднеквадратичного значения амплитуды сигнала к среднеквадратичному значению пикового побочного спектрального состава, измеренного в первой зоне Найквиста от 0 до fs/2. На графике SFDR строится как функция амплитуды сигнала и может быть выражен относительно амплитуды сигнала (дБс) или полной шкалы АЦП (dBFS), как показано на рис. 12.12.

Для сигнала, имеющего амплитуду, близкую к полной шкале АЦП, пиковая спектральная линия определяется несколькими первыми гармониками основной частоты. Но когда сигнал опускается на несколько дБ ниже полной шкалы, появляются другие спектральные линии, которые не являются прямыми гармониками входного сигнала. Это происходит из-за дифференциальной нелинейности передаточной функции АЦП. Поэтому, SFDR учитывает все источники искажения, независимо от их происхождения. Увеличение разрешающей способности АЦП может увеличивать отношение сигнал/шум АЦП, но не обязательно улучшает его SFDR.

 

 

Рисунок 12.12 – Свободный от гармоник динамический диапазон (SFDR)

 

Наиболее популярные АЦП для приложений цифровой обработки сигналов базируются на пяти основных архитектурах: АЦП последовательного приближения, сигма-дельта АЦП, АЦП параллельной обработки, АЦП конвейерной обработки и АЦП последовательного счета.

 

АЦП ПОСЛЕДОВАТЕЛЬНОГО ПРИБЛИЖЕНИЯ

АЦП последовательного приближения много лет были главным инструментом преобразования сигнала. Недавние усовершенствования разработчиков расширили диапазон частот дискретизации этих АЦП до мегагерц. Основные элементы АЦП последовательного приближения представлены на рис. 12.13. Этот АЦП выполняет преобразования в командном режиме. После подачи команды НАЧАТЬ ПРЕОБРАЗОВАНИЕ устройство выборки-хранения УВХ устанавливается в режим хранения, и все разряды регистра последовательного приближения РПП (SAR) сбрасываются в "0", кроме старшего значащего разряда (MSB), который устанавливается в "1". Выходной сигнал регистра последовательного приближения (РПП) подается на внутренний ЦАП.

 

 

Рисунок 12.13 – АЦП последовательного приближения

 

Если выходной сигнал ЦАП больше, чем аналоговый входной сигнал, старший разряд РПП сбрасывается, в противном случае он остается установленным. Затем следующий старший значащий разряд устанавливается в "1". Если сигнал на выходе ЦАП больше, чем аналоговый входной сигнал, старший разряд РПП сбрасывается, в противном случае бит остается установленным. Описанный процесс поочередно повторяется для каждого разряда. Когда все разряды, в соответствии с входным сигналом, будут установлены в "0" или в "1", содержимое регистра последовательного приближения придет в соответствие с значением аналогового входного сигнала, и преобразование завершится. Если рассматриваемый АЦП имеет выход в виде последовательного порта, то последовательно поступаемые биты можно непосредственно передавать на выход. Окончание преобразования индицируется сигналами end-of-convert (EOC), data-ready

(DRDY) или BUSY (фактически, отсутствие сигнала BUSY индицирует окончание преобразования). Полярности и наименование этого сигнала могут отличаться для различных АЦП последовательного приближения, но основная концепция сохраняется. Вначале интервала преобразования логический уровень сигнала высокий (или низкий) и остается в этом состоянии, пока преобразование не закончено. Затем уровень сигнала становиться низким (или высоким). Фронт сигнала индицирует наличие выходных данных.

N-разрядное преобразование осуществляется за N шагов. На первый взгляд может показаться, что 16-разрядному преобразователю для выполнения преобразования требуется в два раза больше времени, чем 8-разрядному преобразователю, но это не так. В 8-разрядном преобразователе перед принятием решения о значении очередного бита ЦАП должен установить на своем выходе сигнал с точностью, соответствующей 8 разрядам, в то время как ЦАП 16-разрядного преобразователя должен установить сигнала на своем выходе с точностью, соответствующей 16 разрядам, что занимает значительно больше времени. На практике 8-разрядный АЦП последовательного приближения может затрачивать на преобразование несколько сотен наносекунд, в то время как 16-разрядному АЦП требуется несколько микросекунд.

Общая точность и линейность АЦП последовательного приближения определяется, прежде всего, внутренним ЦАП. До недавнего времени в большинстве прецизионных АЦП последовательного приближения для достижения желательной точности и линейности использовалась тонкопленочная лазерная подгонка. Процесс подстройки тонкопленочного резистора увеличивает стоимость системы, а значение сопротивления тонкопленочного резистора может измениться при механическом воздействии на корпус микросхемы. По этим причинам в более новых АЦП последовательного приближения стали популярными ЦАП с коммутируемыми конденсаторами (или конденсаторами с перераспределением заряда). Преимущество ЦАП с коммутируемыми конденсаторами состоит в том, что их точность и линейность определяются, прежде всего, качеством фотолитографии, которое, в свою очередь, зависит от площади конденсаторных пластин, емкости и соотношения емкостей конденсаторов. Кроме того, для достижения высокой точности и линейности конденсаторы малой емкости могут подключаться параллельно основным конденсаторам или отключаться от них в соответствии с алгоритмом автокалибровки без необходимости применения тонкопленочной лазерной подстройки.

 

 

Рисунок 12.14 – Временные диаграммы работы АЦП последовательного приближения

Необходимо также отметить, что некоторые АЦП последовательного приближения дополнительно к команде CONVERT START требуют внешней высокочастотной синхронизации, хотя в большинстве случаев необходимости в двух синхронизаторах нет. Частота внешнего синхронизатора, если он требуется, находится в диапазоне от 1 МГц до 30 МГц в зависимости от времени преобразования и разрешающей способности АЦП. В других АЦП последовательного приближения есть внутренний генератор, который используется для выполнения преобразования и требует только команды CONVERT START. Благодаря своей архитектуре, АЦП последовательного приближения допускают любую скорость повторения однократного преобразования, от 0 до максимального быстродействия преобразователя.

 

ПАРАЛЛЕЛЬНЫЕ АЦП

Параллельные АЦП (Flash АЦП) являются самым быстрым типом АЦП, использующим большое количество компараторов, работающих параллельно. N-разрядный параллельный АЦП состоит из 2N резисторов и 2N–1 компараторов, размещенных, как это показано на рис. 12.15. На каждый компаратор подается опорное напряжение, значение которого для соседних точек отличается на величину, соответствующую одному младшему значащем разряду (LSB) (более старшие разряды — в верхних по схеме элементах). При фиксированном входном напряжении все компараторы, размещенные на схеме ниже некоторой точки, имеют входное напряжение выше опорного напряжения. На их логическом выходе присутствует "1". У всех же компараторов выше этой точки опорное напряжение больше входного, и их логический выход установлен в "0". Поэтому 2N–1 выходов компаратора ведут себя аналогично ртутному термометру, и выходной код такого АЦП иногда называют «кодом термометра». В действительности, было бы непрактично выводить 2N–1 линий данных наружу, поэтому они преобразуются приоритетным шифратором в N-разрядный двоичный код.

Входной сигнал подается на все компараторы сразу, поэтому "выход термометра" имеет задержку по отношению к входному сигналу, равную задержке только одного компаратора и N-разрядного кодера. Это соответствует задержке нескольких логических элементов, так что процесс преобразования осуществляется очень быстро. Но такая архитектура предполагает использование большого числа резисторов и компараторов, имеет ограничение по максимальной разрешающей способности и, чтобы обеспечить высокое быстродействие, каждый компаратор должен иметь довольно высокий уровень потребления энергии. Следовательно, к проблемам параллельных АЦП относятся ограниченная разрешающая способность, высокий уровень рассеивания энергии вследствие большого количества высокоскоростных компараторов (особенно на частотах дискретизации больших, чем 50 MSPS) и относительно большие размеры кристалла (и потому — высокая стоимость). Кроме того, для питания быстрых компараторов необходимым током смещения, цепочка опорных резисторов должна иметь низкое сопротивление, чтобы этот источник давал весьма большие токи (> 10 мА).

На практике реализуются преобразователи до 10-разрядов, но обычно параллельные АЦП имеют разрешающую способность, соответствующую 8-разрядам. Их максимальная частота дискретизации может достигать 1 ГГц при ширине полосы пропускания по уровню полной мощности более 300 МГц.

 

 

Рисунок 12.15 – Параллельный АЦП

 

КОНВЕЙЕРНЫЕ АЦП

Хотя целесообразность построения параллельных АЦП с высоким разрешением (большим, чем 10-разрядов) вызывает сомнения, такие АЦП часто используются в качестве подсистем конвейерных (subranging) АЦП (иногда называемых полупараллельными (half-flash)АЦП), которые обладают значительно более высокой разрешающей способностью (до 16-разрядов).

Блок-схема 8-разрядного конвейерного АЦП на основе двух параллельных 4-разрядных АЦП показана на рис. 12.16. Учитывая широкую распространенность 8-разрядных параллельных преобразователей с высокими частотами дискретизации, пример такого преобразователя мы используем для иллюстрации концепции. Процесс преобразования осуществляется в два этапа. Первые четыре старших разряда (MSB) оцифровываются первым параллельным АЦП (обладающим точностью выше 8 разрядов), и двоичный выходной 4-разрядный код подается на 4-разрядный ЦАП (также обладающий точностью выше 8 разрядов). Выходной сигнал с ЦАП вычитается из сохраненного аналогового входного сигнала, и результат вычитания (остаток) усиливается и подается на второй параллельный АЦП. Затем выходные сигналы двух 4-разрядных параллельных преобразователей объединяются в один 8-разрядный выходной код. Если динамический диапазон остаточного сигнала не точно заполняет динамический диапазон второго параллельного преобразователя, возникает нелинейность и, возможно, потеря кода.

 

 

Рисунок 12.16 – 8-разрядный конвейерный АЦП