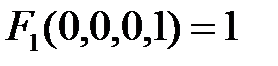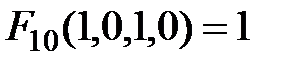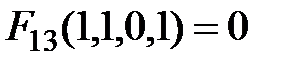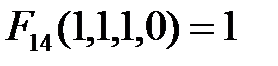Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 3. Минимизация логических функцийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Одной из основных задач, возникающих при синтезе схем цифровых устройств, является минимизация логических функций, которые она реализует. Чем проще логические выражения, описывающие функции, тем проще и дешевле реализующая их цифровая схема. Существует два основных “ручных” метода минимизации логических функций: 1. Аналитический метод с использованием законов и правил алгебры логики. 2. Табличный метод, при котором функция представляется в виде карты Карно (диаграммы Вейча). Аналитический метод минимизации базируется на отыскании соседних элементов в записи функции и их объединении на основании законов алгебры логики. Два минтерма Ki (ν) и Kj (ν) (макстерма Мi (ν) и Mj (ν)) называются соседними, если они различаются только одним первичным термом Пусть задана СКНФ функции трех переменных F (ν) = K 0(ν) Ú K 2(ν) Ú Ú K 3(ν) Ú K 6(ν) =
Уже из этого элементарного примера видно, что аналитический метод достаточно сложен в силу трудоемкости поиска соседних минтермов. Табличный метод минимизации логической функции базируется на использовании диаграммы Вейча (карты Карно), которая является одним из способов табличного задания функции и состоит из клеток, каждая из которых соответствует определенной точке ν i области определения функций, т. е. диаграммы Вейча для функции n переменных состоят из 2 n клеток, которые можно пронумеровать числами i = 0, 1,..., 2 n – 1. Чтобы с помощью диаграммы Вейча задать функцию F (ν), необходимо в каждую клетку с номером i занести значение функции F (ν i) = аi = 0 или 1, которое она принимает в точке i. Таким образом, одна строка таблицы истинности функции в диаграмме Вейча представляется одной ячейкой.
Для составления диаграммы Вейча (карты Карно) рисуется таблица, ее строки и столбцы нумеруются в двоичном коде и им присваиваются переменные. Вид диаграммы Вейча и карты Карно для функции четырех переменных представлен на рисунке 3.1. Здесь для наглядности координаты клеток указаны в трёх формах: в виде соответствующего минтерма; в виде двоичного числа, соответствующего порядковому номеру наборов аргументов; в десятичном эквиваленте номеров наборов аргументов.
а)
б) Рисунок 3.1 – Вид диаграммы Вейча (а) и карты Карно для функции четырех аргументов
Следует отметить, что диаграмма Вейча отличается от карты Карно только в способе обозначения строк и столбцов. В диаграмме Вейча строки и столбцы пронумерованы в порядке нарастания двоичных чисел (00, 01, 10, 11), а в карте Карно – последовательностью чисел в коде Грея (00, 01, 11, 10), что делает все клетки карты Карно соседними. Это свойство определяет более широкое применение при минимизации функции именно карты Карно. Для представления логической функции картой Карно необходимо последнюю заполнить единицами и нулями согласно значениям функции, определяемым ее таблицей истинности либо логическим выражением. Для минимизации функции единицы в карте объединяются замкнутыми контурами в группы по правилам: 1. Число единиц в группе должно быть 2. Внутри контура должны быть только клетки, заполненные единицами, одна и та же клетка может входить несколько контуров. 3. Крайние столбцы и строки карты Карно являются соседними и их клетки могут входить в общий контур.
4. Число контуров (групп) должно быть минимальным, охватывая все единичные клетки. 5. При записи минтермов в минимизированной функции исключаются переменные, имеющие взаимоинверсные значения (0 и 1 либо В качестве примера минимизации рассмотрим функцию четырех аргументов, заданную таблицей истинности (таблица 3.1)
Таблица 3.1 – Таблица истинности логической функции
Карта Карно, соответствующая данной функции представлена на рисунке 3.2.
б) Рисунок 3.2 – Карты Карно для функции
Объединяем единичные клетки в группы и записываем результат минимизации в минимальной ДНФ:
Основная задача минимизации не полностью определенных функций заключается в отыскании оптимального варианта ее доопределения, позволяющего получить минимальную из всех возможных ДНФ или КНФ. Если значения функции не заданы в m точках, то ее можно доопределить 2 m способами. Поэтому минимизация неполностью определенной функции состоит в оптимальном выборе одной из 2 m полностью определенных функций (понятно, что, как и при минимизации полностью определенных функций, может быть получено несколько равноценных МДНФ и МКНФ). Следует иметь в виду, что в результате минимизации неполностью определенных функций всегда получаются полностью определенные функции.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 909; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.79.179 (0.009 с.) |

 (т.е., если один из минтермов содержит
(т.е., если один из минтермов содержит  , а другой
, а другой 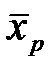 , все же остальные первичные термы одинаковые). Так, например, минтермы K 2(ν) =
, все же остальные первичные термы одинаковые). Так, например, минтермы K 2(ν) =  и K 6(ν) = =
и K 6(ν) = =  являются соседними, так как они различаются только одним первичным термом
являются соседними, так как они различаются только одним первичным термом  . Для минтерма K 2(ν) соседними будут также минтермы K 0(ν) =
. Для минтерма K 2(ν) соседними будут также минтермы K 0(ν) = 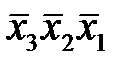 , K 3(ν) =
, K 3(ν) =  . Очевидно, что каждый минтерм (макстерм) n переменных Ki (ν) имеет по n соседних минтермов (макстермов) из общего числа 2 n. На основании свойств дизъюнкции и конъюнкции один и тот же минтерм (макстерм), входящий в СДНФ (СКНФ) может использоваться несколько раз для объединения с соседними минтермами (макстермами).
. Очевидно, что каждый минтерм (макстерм) n переменных Ki (ν) имеет по n соседних минтермов (макстермов) из общего числа 2 n. На основании свойств дизъюнкции и конъюнкции один и тот же минтерм (макстерм), входящий в СДНФ (СКНФ) может использоваться несколько раз для объединения с соседними минтермами (макстермами). . Здесь для минимизации минтерм K 2(ν) =
. Здесь для минимизации минтерм K 2(ν) = 


 0 0 0 0
0 0 0 0
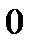
 0 0 0 1
0 0 0 1
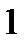
 0 0 1 0
0 0 1 0
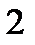
 0 0 1 1
0 0 1 1

 0 1 0 0
0 1 0 0

 0 1 0 1
0 1 0 1

 0 1 1 0
0 1 1 0

 0 1 1 1
0 1 1 1

 1 0 0 0
1 0 0 0

 1 0 0 1
1 0 0 1

 1 0 1 0
1 0 1 0
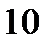
 1 0 1 1
1 0 1 1

 1 1 0 0
1 1 0 0

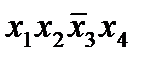 1 1 0 1
1 1 0 1

 1 1 1 0
1 1 1 0

 1 1 1 1
1 1 1 1
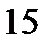
 , где k = 0, 1, 2, 3…, следовательно, допустимое число клеток в контуре 1, 2, 4, 8,…
, где k = 0, 1, 2, 3…, следовательно, допустимое число клеток в контуре 1, 2, 4, 8,… и
и  ).
).