
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод штрафных функций и барьерных функцийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Совершенно иной подход используется в методах штрафных и барьерных функций. Ограничения задачи специальным образом отражаются в критерии, в результате чего критерий модифицируется, а исходная задача на условный экстремум сводится к задаче на безусловный экстремум. В методе штрафных функций в критерий вводится штраф при нарушении условий задачи. Пусть в общем случае имеем задачу f (x) à min; (8.65) ji (x) £ 0, yi (x) = 0, Тогда можно построить вспомогательную функцию Q (x) = f (x) + a × H (x), (8.68) где H (x)–функция штрафа, a - параметр штрафа. Вспомогательная функция играет роль модифицированного критерия, который при выполнении всех ограничений должен совпадать с исходным. Поэтому необходимо, чтобы в допустимой области Н (х) равнялась нулю, а вне ее была положительной. Для задачи (8.65)-(8.67) функция штрафа включает две составляющие Н (х) = Нj (x) + Нy (x), учитывающие ограничения-неравенства и ограничения-равенства соответственно и удовлетворяющие условиям
Возможны разные конструкции функций, обладающих указанными свойствами. Типичные представители составляющих штрафной функции имеют вид
где р – натуральное число. Для дифференцируемости функций берут четные значения р, обычно р = 2. Чем больше a, тем сильнее влияет функция штрафа и, значит, тем точнее выполняются условия задачи. Пример 8.8. Дана задача f (x) = x à min; j (x)=3 – x £ 0. Ответ очевиден: x *=3. Теперь сведем эту задачу к определению безусловного экстремума вспомогательной функции. Построим штрафную функцию в соответствии с (8.69): H = [max (0, 3-x)]2. Тогда приходим к задаче Q = x + a [max (0, 3-x)]2® min.
Находим минимум этой функции:
Отсюда получаем Пример 8.9. Рассмотрим влияние параметра шага в задаче
Здесь
Таким образом, чтобы безусловный минимум вспомогательной функции был близок к условному минимуму решаемой задачи, необходимо брать очень большое значение a, теоретически бесконечное. Однако при больших a возникают серьезные трудности при поиске минимума вспомогательной функции. Поэтому предлагается решать последовательность задач минимизации Q с возрастающими значениями a. При этом в качестве начальной точки следующей задачи берется оптимальная точка предыдущей. Такой прием использован в следующем алгоритме штрафных функций. Алгоритм. 1. Задать: начальную точку x 0, точность e, начальное значение a 0 и число b > 1. 2. Минимизировать Q (x) одним из методов безусловной оптимизации, в результате чего определяется 3. Проверить: если 4. Положить Рекомендуется выбирать значения параметров алгоритма из диапазонов: a 0Î(0,1], b Î(1,10]. Начальную точку следует задавать в недопустимой области. Пример 8.10. Алгоритмом штрафных функций решить задачу
Возьмем начальную точку x 0=(-5;5), a 0=0,21, b =5 и e =0,0001. Применяя для минимизации Q метод Ньютона, получаем результаты, представленные в табл. 8.4. Таблица 8.4
Другой пример поиска методом штрафных функций приведен на рис. 8.45 для задачи
Поиск проведен из начальной точки (-2;-7) с параметрами a 0=0,1 и b =2. Здесь, как и в предыдущем примере, на первой итерации алгоритма движение направлено в сторону безусловного минимума целевой функции. Это объясняется небольшим начальным значением параметра штрафа, при котором основное влияние на направление оказывает целевая функция. С возрастанием a направление поиска ориентируется на условный экстремум.
Таким образом, выбор параметров поиска имеет существенное влияние на эффективность алгоритма. Метод барьерных функций В отличие от метода штрафных функций, данный метод применим к задачам с ограничениями только в виде неравенств. Суть метода заключается в том, что поиск начинается обязательно из внутренней точки и последующие точки не должны выходить из допустимой области. С этой целью задача модифицируется так, что при приближении к границе допустимой области растет барьер, препятствующий выходу на границу. Исходная задача на условный экстремум задается в виде f (x) à min; (8.70) ji (x) £ 0, Она преобразуется в задачу безусловной минимизации вспомогательной функции Q (x) = f (x) + mB (x), где B (x) – барьерная функция, m - параметр барьера. Обязательное условие: внутренность области не должна быть пустой (имеются точки, в которых " ji (x) < 0). Барьерная функция строится так, чтобы она была неотрицательной и непрерывной на допустимом множестве и стремилась к бесконечности при приближении изнутри к границе:
Как и в случае штрафной функции, существует несколько конструкций B (x), удовлетворяющих этим условиям. Но в основном используется барьерная функция в виде
Понятно, что решение вспомогательной задачи зависит от значения параметра барьера. Покажем на задаче из примера 8.7 влияние m на результат минимизации Q. Пример 8.11. Исходная задача: f (x) = x à min; j (x)=3 – x £ 0. Барьерную функцию строим согласно (8.72). Тогда вспомогательная функция имеет вид
Находим точку минимума Q:
Отсюда получаем
Следовательно, с уменьшением m точки минимума вспомогательной функции приближаются к минимуму исходной задачи. Геометрическая иллюстрация решения приведена на рис. 8.47. Как хорошо видно на рис. 8.47, при оптимуме исходной задачи на границе допустимого множества последовательность точек минимума Q с у меньшением m приближается к оптимальному решению изнутри допустимой области. По этой причине метод барьеров называют еще методом внутренних штрафов. В связи с возможными трудностями поиска при малых значениях m решается не одна, а последовательность вспомогательных задач с уменьшающимися значениями параметра барьера.
1. Выбрать начальную точку x 0 так, чтобы " ji (x 0)<0; задать точность e, начальное значение m 0 и число b Î (0, 1). 2. Минимизировать Q (x) одним из методов безусловной оптимизации, в результате чего определяется 3. Проверить: если 5. Положить Значение m 0 можно брать из интервала [2, 10]. Важное замечание касается п.2 алгоритма: в процессе поиска минимума вблизи границы из-за дискретности шагов возможен выход за допустимую область, где барьерная функция становится отрицательной, что повлечет расхождение поиска. Поэтому необходима явная проверка на допустимость точек на каждом шаге при минимизации Q. Пример 8.10 (Базара, Шетти). Исходная задача: f (x) = (x 1 - 2)4+(x 1-2 x 2)2® min; j (x)= Решение находим, используя соответствующую вспомогательную функцию Q =(x 1 - 2)4+(x 1-2 x 2)2 - За начальную точку возьмем допустимую точку (0;1), значения m и b принимаем равными 10. Результаты поиска алгоритмом барьерных функций представлены в табл. 8.5 и на рис. 8.48.
Таблица 8.5
Завершая рассмотрение методов штрафных и барьерных функций, отметим, что можно построить алгоритм, использующий как штрафы, так и барьеры. Для этого достаточно записать смешанную вспомогательную функцию в виде Q (x) = f (x) + mB (x) +
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 2316; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.008 с.) |

 ; (8.66)
; (8.66) . (8.67)
. (8.67) (8.69)
(8.69)

 На рис. 8.41 и 8.42 показаны функции aH и Q для двух значений a. Видно, что точки минимума вспомогательной функции с увеличением a приближаются к точке условного минимума исходной задачи. Такой же вывод следует из аналитического решения. Действительно, при x <3 вспомогательная функция имеет вид
На рис. 8.41 и 8.42 показаны функции aH и Q для двух значений a. Видно, что точки минимума вспомогательной функции с увеличением a приближаются к точке условного минимума исходной задачи. Такой же вывод следует из аналитического решения. Действительно, при x <3 вспомогательная функция имеет вид


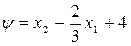 и
и  На рис. 8.43 построены линии уровня функции q для разных значений a и линия ограничения y. При a =0 имеем q = f,и минимум q достигается в точке безусловного минимума f: x 1= x 2=1. С увеличением a меняется форма линий уровня q и положение минимума. При a =1 минимум q смещается к линии ограничения, а при a =1000 он практически точно совпадает с условным минимумом задачи.
На рис. 8.43 построены линии уровня функции q для разных значений a и линия ограничения y. При a =0 имеем q = f,и минимум q достигается в точке безусловного минимума f: x 1= x 2=1. С увеличением a меняется форма линий уровня q и положение минимума. При a =1 минимум q смещается к линии ограничения, а при a =1000 он практически точно совпадает с условным минимумом задачи.
 .
. , то остановиться, приняв
, то остановиться, приняв  за оптимальное решение задачи.
за оптимальное решение задачи. , за начальную точку принять
, за начальную точку принять 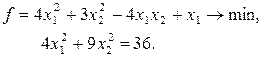
 Как следует из таблицы, решение с заданной высокой точностью получено за 11 итераций алгоритма. Заметим, что несмотря на увеличение a значение aH сходится к нулю, обеспечивая сходимость алгоритма. Траектория поиска и линии уровня функции f изображены на рис. 8.44.▲
Как следует из таблицы, решение с заданной высокой точностью получено за 11 итераций алгоритма. Заметим, что несмотря на увеличение a значение aH сходится к нулю, обеспечивая сходимость алгоритма. Траектория поиска и линии уровня функции f изображены на рис. 8.44.▲
 Еще один пример поиска показан на рис. 8.46 для задачи
Еще один пример поиска показан на рис. 8.46 для задачи
 Здесь поиск производился при a 0=1 и b =10. Такие параметры обусловили другой характер движения к условному минимуму: первая итерация уже не приводит в окрестность безусловного экстремума и траектория не имеет резких изменений направления поиска.
Здесь поиск производился при a 0=1 и b =10. Такие параметры обусловили другой характер движения к условному минимуму: первая итерация уже не приводит в окрестность безусловного экстремума и траектория не имеет резких изменений направления поиска. . (8.71)
. (8.71)
 (8.72)
(8.72)



 , то остановиться, приняв
, то остановиться, приняв  , за начальную точку принять
, за начальную точку принять  x 2£ 0.
x 2£ 0.
 Как и следовало ожидать, с уменьшением m значение mB стремится к нулю.
Как и следовало ожидать, с уменьшением m значение mB стремится к нулю.
 где барьерная функция B (x) применяется к неравенствам, а штрафная функция Н (х) – к ограничениям-равенствам. Последовательность задач минимизации Q решается с уменьшающимися значениями параметра m.
где барьерная функция B (x) применяется к неравенствам, а штрафная функция Н (х) – к ограничениям-равенствам. Последовательность задач минимизации Q решается с уменьшающимися значениями параметра m.


