
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача о максимальном потокеСодержание книги
Поиск на нашем сайте Наибольший интерес представляет постановка задачи, в которой критерием является поток сети: Z ® max; (5.34)
0£ xij £ dij. (5.37) Задача (5.34) – (5.37) называется задачей о максимальном потоке. Она имеет большое практическое значение. Для нее разработаны алгоритмы, которые эффективнее методов решения транспортных задач. Они работают непосредственно с сетью как разновидностью графов. В связи с этим напомним понятие разреза графа (сети), которое используется в основополагающей теореме Форда-Фалкерсона. Пусть дан ориентированный граф G= (V,U), где V и U -множества вершин и дуг соответственно. Разрезом сети на подмножестве вершин A Ì V, A ¹Æ, A ¹ V, tÎ A, sÎ V\A называется множество дуг ij Î U таких, что i Î A & j Î V\A. Обозначим его P(A). Сумма пропускных способностей дуг разреза называется величиной (пропускной способностью) разреза:
Пример 5.5. Построим один из разрезов сети, приведенной на рис.5.7.
Разрез сети, имеющий минимальную пропускную способность, называется минимальным разрезом. Можно показать, что задачи максимизации потока и минимизации величины разреза являются двойственной парой. Из этого факта следует Величина потока сети (от истока к стоку) не превосходит пропускной способности минимального разреза и существует максимальный поток, величина которого равна пропускной способности минимального разреза. Методы решения задачи о максимальном потоке основаны на последовательном увеличении потока при соблюдении условий (5.35)-(5.37). При этом легко увидеть аналогию с перемещением по циклу в методах решения транспортных задач. Аналогом цикла пересчета является увеличивающая цепь. Это цепь, соединяющая исток и сток, все дуги которой допустимые. Дуга является допустимой увеличивающей, если ее направление совпадает с направлением потока и поток на ней меньше пропускной способности, то есть xij<dij. Дуга считается допустимой уменьшающей, если направление дуги противоположно потоку и xij > 0. На увеличивающей дуге поток может возрасти на величину qij=dij-xij, а на уменьшающей дуге возможно снижение потока, равное qij = xij. Следовательно, максимальное допустимое изменение величины потока по увеличивающей цепи определяется как минимальное из возможных: q0 = Таким образом, максимальный поток сети может быть определен по следующему алгоритму. 5. Задать начальную величину потока, обеспечиваемую потоками дуг при выполнении условий (5.35)-(5.37). Примечание. Очевидно, что в качестве начального всегда можно взять нулевой поток. 6. Построить увеличивающую цепь. Если построить невозможно, то решение завершено. 7. По формуле (5.38) вычислить q0. 8. Переместить вдоль цепи q0, прибавляя к потокам на увеличивающих дугах и вычитая из потоков уменьшающих дуг. В результате поток сети увеличивается на q0. Перейти на шаг 2.
Пример 5.6. Определить максимальный поток сети на рис. 5.8. Пропускные способности дуг показаны у стрелок перед косой чертой. Задаем начальный поток. Значения начальных потоков дуг даны за косой чертой, они удовлетворяют условиям задачи. Величина потока сети Z (0)=7. Первая итерация. Строим увеличивающую цепь. Она показана на рис. 5.8 утолщенными линиями. Определяем приращение потока: q0 = min(7-3, 5-1, 6-4)=2. Увеличиваем потоки дуг цепи на 2 (рис. 5.9). Z (1)= Z (0) + q0 =7+2=9.
Вторая итерация.
Строим увеличивающую цепь {t,1; 1,4; 4,s} (рис. 5.9). q0 = min(7-5, 3-2, 5-1)=1.Увеличиваем потоки по дугам цепи на q0 (рис. 5.10). Z (2)= Z (1) + q0 = 9+1=10. Третья итерация. Новая цепь состоит из увеличивающих дуг t,3 и 4,s и уменьшающей дуги 4,3 (рис. 5.10). q0 = min(4-2, 1, 5-2)=1. Изменяем потоки: на дугах t,3 и 4,s увеличиваем, а на дуге 4,3 уменьшаем на величину q0. Тогда получаем Z (3)= Z (2) + q0 = 10+1=11 (рис. 5.11).
Так как увеличивающую цепь построить нельзя, последнее решение является оптимальным. Максимальный поток сети равен 11.Минимальный разрез рассмотренной сети соответствует множеству вершин А ={t,1,2,3,5,6}, то есть P(A)={1,4; 5,s; 6,s}. Его пропускная способность d (A)= d14+d5s+d6s =3+2+6=11 равна величине максимального потока, что согласно теореме Форда-Фалкерсона также является признаком оптимальности найденного решения.
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 508; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.007 с.) |

 k ¹ t, k ¹ s; (5.35)
k ¹ t, k ¹ s; (5.35)  (5.36)
(5.36)
 Если A ={t,1,2,3}, то разрезом будет множество дуг P(A)={1,4; 1,6; 2,5; 3,6}, а его величина определяется как d (A)= d14+d16+d25+d36. Дуги, составляющие этот разрез, выделены жирными линиями.▲
Если A ={t,1,2,3}, то разрезом будет множество дуг P(A)={1,4; 1,6; 2,5; 3,6}, а его величина определяется как d (A)= d14+d16+d25+d36. Дуги, составляющие этот разрез, выделены жирными линиями.▲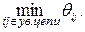 (5.38)
(5.38)






