
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение начального базисного решенияСодержание книги
Поиск на нашем сайте Симплекс-метод основан на переходах от одного допустимого базисного решения к другому (смежному). Как показано ранее, базисное решение включает m неотрицательных переменных, называемых базисными, при нулевых значениях остальных (небазисных или свободных) переменных. Чтобы начать движение к оптимуму, необходимо иметь начальное базисное решение. Оно может быть получено из модели, представленной в канонической форме. При этом выбор базисных переменных зависит от вида условий исходной модели, но в любом случае каждому условию соответствует своя базисная переменная (предполагается линейная независимость m условий). Рассмотрим возможные варианты построения начального решения. 1. Исходная модель представлена неравенствами “£”:
Для приведения к каноническому виду в каждое неравенство вводится дополнительная переменная:
Если положить xj =0, j =1,2,…, n, то дополнительные переменные xn+i = bi ³0 (i =1,2,…, m) удовлетворяют всем требованиям допустимого базисного решения: выполняются все условия задачи и число базисных переменных равно m. Очевидно, что этому базисному решения соответствует единичный базис { Ai }(0) = { An+ 1, An+ 2 ,…,An+m }. В этом случае не надо вычислять коэффициенты разложения небазисных векторов по базису. Действительно, в системе уранений
каждый коэффициент входит только в одно уравнение с множителем +1. Поэтому ее решением будет an+i,j = aij, то есть коэффициенты разложения равны соответствующим компонентам раскладываемого вектора условий. 2. Исходная модель представлена неравенствами “³”:
Тогда соответствующая каноническая модель
включает дополнительные переменные со знаком “минус”. Если из них образовать базисное решение, то оно будет недопустимым, так как из модели следует В этом случае строится искусственное базисное решение, в котором все переменные неотрицательные, но не выполняется часть функциональных ограничений. Здесь возможны два варианта. В первом из них в каждое равенство канонической модели вводится искусственная переменная
Полагая все исходные и дополнительные переменные равными нулю, получаем искусственное базисное решение Этот прием очень простой, но приводит к значительному увеличению числа переменных. Второй вариант устраняет этот недостаток. Найдем в канонической модели уравнение с наибольшей правой частью. Пусть таким будет последнее уравнение, то есть.
Вычитая из него по отдельности каждое уравнение (кроме его самого), получаем преобразованную систему
где
Если теперь положить xj =0 (j =1,2,..., m) и xn+m =0, то дополнительные переменные xn+i=b`i ³0 (i =1,2,…, m -1) могут быть приняты в качестве базисных. Однако при этом нехватает одной базисной переменной и последнее уравнение не выполняется. Введем в него искусственную переменную xm+n+ 1 которая и будет недостающей базисной переменной (xm+n+ 1 =bm). Таким образом, получено искусственное базисное решение, содержащее независимо от числа ограничений только одну искусственную переменную. Соответствующий ему базис, как и ранее, является единичным:
При переходе от одного базисного решения к другому допустимое решение достигается только тогда, когда все искусственные переменные станут равными нулю. Для ускорения вывода этих переменных из числа базисных (обнуления) рекомендуется придавать им большой негативный вес путем модификации критерия:
где М - большое положительное число, такое, что M >>max| C j| (в задаче на минимум знак минус заменяется на плюс). Если при выполнении признака оптимальости хотя бы одна исксственная перемнная останется положительной, то это будет означать, что задача неразрешима из-за противоречивости условий: не выполняться будут те условия, в которые входят ненулевые искуссвенные переменные. 3.В исходной модели условия заданы в виде равенств
Для построения базисного решения введем в каждое равенство искусственную переменную:
Тогда базисное решение будет состоять из искусственных переменных
Число искусственных переменных может быть меньше, если в исходной системе есть переменные, входящие со знаком плюс только в одно уравнение. Такие переменные принимаются за базисные, а искусственные переменные в соответствующие условия не вводятся.. 4.Исходная модель содержит все виды ограничений (общий случай). Предварительно условия группируются по виду. В каждой группе определяются базисные переменные одним из способов, описанных выше. Очевидно, что при таком подходе начальный базис будет единичным и, следовательно, не потребуется вычислять коэффициенты разложения небазисных векторов в начальном решении Алгоритм симплекс-метода Резюмируя изложенное в предыдущих разделах, опишем алгоритм симплекс-метода. По модели в каноническом виде определяется начальное базисное решение. Последующие действия проводятся в специальных таблицах, называемых симплекс-таблицами. В них представляются результаты итераций, которые завершаются при выполнении признака оптимальности или обнаружении неразрешимости задачи. Полная симплекс-таблица имеет следующую структуру.
Здесь Cj – коэффициенты линейной формы L, Csi – коэффициенты в L при базисных переменных (подмножество Cj), Asi – базисные векторы, si – индекс базисного компонента на позиции i. Жирной линией выделена главная часть таблицы, все ее элементы подчиняются соотношениям (4.22). Первая и последняя строки и второй столбец таблицы являются вспомогательными, они обязательны только в начальной таблице. Примечание. В линейной алгебре во второй строке и третьем столбце таблицы используют обозначения переменных xj и xi вместо векторов Aj и Asi соответственно. Поскольку элементы главной части таблицы являются коэффициентами разложения векторов, принятые здесь обозначения, на наш взгляд, более корректны. Алгоритм состоит из предварительного и основного этапов. На предварительном этапе сначала определяется начальное базисное решение одним из методов, рассмотренных выше. Исходя из него заполняется начальная симплекс-таблица. В третий столбец заносятся m базисных векторов, а во второй – соответствующие коэффициеты из L (или из верхней строки) в порядке следования условий в модели (на первую позицию ставится вектор при базисной переменной из первого условия и т.д.). Так как начальный базис единичный, элементы главной части таблицы кроме последней строки не вычисляются, а берутся прямо из модели (в столбец A0 заносятся правые части условий, в Aj – коэффициеты при Для получения относительных оценок используются формулы (4.11) и (4.12). Значения zj находятся как скалярное произведение векторов Cb =[ Csi ] и Aj (суммируются произведения одноименных компонент). Вычитая из нижней строки верхнюю, получаем L и оценки Δ j. Основной этап является итерационным. Очередная итерация заканчивается заполнением симплекс-таблицы за исключением столбца q. Пусть завершилась l- я итерация. Цикл начинается с анализа оценок Δj в таблице l. Если нет отрицательных оценок, значит, выполнился признак оптимальности. В этом случае возможны два вывода: 1) если не вводились искусственные переменные или они равны нулю, получено оптимальное решение; 2) если хотя бы одна искусственная переменная не равна нулю, задача неразрешима из-за противоречивости условий. При невыполнении признака оптимальности анализируются столбцы с отрицательными оценками. Если среди них обнаружится столбец, в котором все коэффициенты разложения неположительны, то есть aij £0, " i, то задача неразрешима по причине неограниченности критерия на допустимом множестве. В противном случае выбирается минимальная (отрицательная) оценка
Она определяет столбец Ar, называемый направляющим или разрешающим, или ведущим столбцом. Мы будем придерживаться первого термина. Заполняется столбец q. Значения q вычисляются делением элементов столбца A0 на положительные элементы направляющего столбца
По минимальному значению q определяется направляющая строка k:
На пересечении направляющейстроки и направляющего столбца находится направляющий элемент akr. Тем самым определена переменная Заполняется таблица l+1. В ней отражается смена базиса: вектор Ask заменяется вектором Ar, соответственно вместо Csk ставится Cr, остальные базисные элементы остаются на месте. Элементы главной части таблицы вычисляются согласно (4.22):
После заполнения главной части таблицы возвращаемся на начало основного этапа. Для контроля вычислений можно проводить повторный счет оценок, используя вспомогательные строки z и C. Наглядное представление алгоритма дает блок-схема, приведенная на рис. 4.8. Замечание. При выборе направляющего столбца и направляющей строки может иметь место неоднозначность из-за достижения минимума более чем на одном индексе. При этом можно выбирать любой из них либо для однозначного выбора добавить правило, например, при нескольких индексах брать наименьший. Из неоднозначности выбора строки следует, что новое базисное решение будет вырожденным. При степени вырожденности больше единицы теоретически возможно зацикливание. Для его устранения в теории предложена e-задача, соответствующая малому деформированию вектора ограничений, которое приводит к замене вырожденной вершины невыржденными. Из решения этой задачи выведено более сложное правило выбора направляющей строки: В строках с минимальным q находятся отношения q 1 элементов 1-го столбца к элементам направляющего и выбирается строка с минимальным q 1. Если же этот выбор снова неоднозначен, то вычисляются отношения q 11 элементов 2-го и направляющего столбца в строках с минимальным q 1, и т.д. до достижения однозначного выбора. Это правило гарантирует от зацикливания. Однако на реальных задачах сталкиваться с зацикливанием не приходилось, и поэтому изложенное правило представляет больше теоретический интерес. Двойственность задач ЛП Любой задаче ЛП можно поставить в соответствие другую задачу, называемую сопряженной или двойственной. При этом исходную задачу называют прямой. Выделяют общий и симметричный случаи двойственности. Если в прямой задаче все условия представлены в виде неравенств и все переменные ограничены по знаку, то имеет место симметричная пара двойственных задач. Когда в исходной задаче есть равенства и/или переменные, которые не ограничены по знаку, то говорят об общем случае двойственности (симметрия моделей отсутствует).
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 653; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.011 с.) |

 .
.
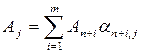
 .
.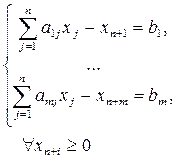

 :
: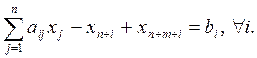
 Очевидно, что в нем все исходные неравенства не выполняются. Векторы с одноименными индексами образуют начальный единичный базис.
Очевидно, что в нем все исходные неравенства не выполняются. Векторы с одноименными индексами образуют начальный единичный базис. .
.


 .
. , для первого варианта,
, для первого варианта, для второго варианта,
для второго варианта,

 базис – из единичных векторов при этих переменных, а исходный критерий модифицируется:
базис – из единичных векторов при этих переменных, а исходный критерий модифицируется:

 ).
).


 которая становися базисной, и переменная
которая становися базисной, и переменная  выводимая из числа базисных (она становится равной нулю).
выводимая из числа базисных (она становится равной нулю).
 Эти формулы применяются следующим образом. Элементы строки, которая была направляющей, находятся делением строки на направляющий элемент. Для вычисления остальных элементов можно использовать правило прямоугольника: в таблице l элемент aij проектируется на направляющий столбец и направляющую строку (рис.4.7). В вершинах образовавшегося прямоугольника находятся все элементы, входящие в рекуррентную формулу. Теперь, вычитая из проектируемого элемента произведение элементов в двух других противолежащих вершинах прямоугольника, деленное на направляющий элемент, получаем новое значение элемента. При этом так вычисляются элементы только небазисных столбцов, так как в базисных столбцах всегда имеем единичные векторы.
Эти формулы применяются следующим образом. Элементы строки, которая была направляющей, находятся делением строки на направляющий элемент. Для вычисления остальных элементов можно использовать правило прямоугольника: в таблице l элемент aij проектируется на направляющий столбец и направляющую строку (рис.4.7). В вершинах образовавшегося прямоугольника находятся все элементы, входящие в рекуррентную формулу. Теперь, вычитая из проектируемого элемента произведение элементов в двух других противолежащих вершинах прямоугольника, деленное на направляющий элемент, получаем новое значение элемента. При этом так вычисляются элементы только небазисных столбцов, так как в базисных столбцах всегда имеем единичные векторы.


