
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Целочисленное программированиеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Целочисленное программирование (ЦП) – это наиболее важный раздел дискретного программирования. Задачи дискретного программирования отличаются тем, что на переменные накладывается требование дискретности, в частном случае – целочисленности. В качестве примеров можно привести задачи о раскрое (разд. 4.11.5), о ранце, коммивояжера и др. Характерные источники целочисленности (дискретности): 1. неделимость объектов, представляемых переменными (например, x – число рабочих или отправляемых вагонов); 2. вариантность типа “да-нет” (например, включать или нет данный пакет в портфель ценных бумаг); 3. заданность возможных значений нормативными документами (например, сечения проводов, диаметров труб, размеров профилей и т.п.); 4. комбинаторность (например, размещение объектов, порядок обхода объектов, упорядочение); 5. логические условия (например, фиксированные затраты имеют место только при производстве продукции). Различают задачи полностью целочисленные/дискретные и частично целочисленные (смешанные). В последних требование целочисленности накладывается не на все переменные.Любой ряд дискретных значений может быть представлен линейной комбинацией целочисленных переменных. Поэтому дискретная задача легко сводится к целочисленной за счет значительного увеличения числа переменных. В этой главе рассматриваются только линейные целочисленные задачи. Проблема целочисленности На первый взгляд может показаться, что целочисленная задача решается проще непрерывной. При малой размерности и узких диапазонах переменных задачу можно решить простым перебором. В других случаях необходимы соответствующие методы. Несмотря на линейность модели допустимое множество целочисленной задачи не является выпуклым. Так, в полностью целочисленной задаче оно представляет собой множество отдельных точек, имеющих целочисленные координаты. Методы линейного программирования базируются на выпуклости допустимого множества и поэтому непосредственно не могут быть применимы к целочисленным задачам. Можно, конечно, пренебречь требованием целочисленности и использовать один из методов ЛП, но тогда, за редким исключением, результат не будет целочисленным. Округление дробных значений переменных проблематично. Действительно, так как оптимальное решение непрерывной задачи лежит в вершине допустимого множества, округление может привести к недопустимости. При двух дробных переменных имеется 4, а при n переменных – 2 n вариантов округления! Какие из них дают допустимые решения, можно определить только после проверки всех ограничений. При этом следует иметь в виду, что, во-первых, целочисленная задача может оказаться неразрешимой несмотря на разрешимость непрерывной задачи; во-вторых, допустимость округленного решения еще не означает его оптимальность. Проиллюстрируем последний тезис известной задачей о садовнике. По расчетам садовника требуется внести в почву комплексные удобрения в количестве 107 кг. Удобрения продаются только в расфасованном виде: 1) мешок весом 35 кг стоит 140 руб.; 2) мешок весом 24 кг стоит 120 руб. Необходимо определить вариант закупки удобрений с минимальными затратами. Запишем модель задачи: L= 140 x1+ 120 x2® min; 35 x1+ 24 x2 ³ 107; x1, x2 ³ 0, int (целые). Если пренебречь целочисленностью, то легко увидеть, что оптимальным будет решение x1= 3 Если округлить его по правилам арифметики, то получим недопустимое решение. Округление в большую сторону (x1= 4, x2= 0)приводит к допустимости, но является ли такое решение оптимальным? Чтобы ответить на этот вопрос, рассмотрим все возможные Таблица 7.1
целочисленные решения (табл.7.1). Прочерк в графе критерия означает недопустимость. Как видно из таблицы, оптимальным является решение x1*= 1, x2*= 3, которое принципиально отличается от непрерывного: закупать надо в основном мешки 2-го типа, тогда как по нерерывному решению – только 1-го типа. Кроме того, округленное допустимое решение оказалось далеким от оптимального: затраты в нем выше минимальных на 12%. ▲ Другую особенность свойств целочисленных задач покажем также на конкретном примере: L= 21 x1+ 11 x2® max; 7 x1+ 4 x2 £ 13; x1, x2 ³ 0, int. Как и в задаче о садовнике, рассмотрим все возможные целочисленные решения. При этом сначала возьмем решение x1= 1, x2= 1 и решения, окружающие его (табл. 7.2). Целочисленные точки и ограничение показаны на рис. 7.1.
Из таблицы следует, что в точке (1, 1) имеет место локальный экстремум, а глобальный максимум достигается в точке (0, 3). В непрерывной линейной задаче любой локальный экстремум является глобальным. То что целочисленная задача может иметь локальные экстремумы, необходимо учитывать при использовании методов частичного перебора. ▲ В ряде случаев решение целочисленной задачи находят, решая ее как непрерывную. Так, если в оптимальном решении непрерывной задачи нецелочисленные значения переменных велики (их порядок >102), округление до целых оправдано: возможные нарушения условий и отклонение от оптимальности пренебрежимо малы. При особых свойствах целочисленной задачи решение ее как непрерывной всегда дает целочисленный результат. Такой исход имеет место, если все вершины допустимого множества целочисленные. Многогранное множество, обладающее этим свойством, называется целочисленным. Определим условия, при которых множество оказывается целочисленным. Возьмем многогранное множество M (B):
где все aij – фиксированные целые числа, B = (b 1 ,b 2,…, bm)Т и m<n (ранг матрицы [ aij ] равен m.) Для него справедлива следующая теорема. Теорема. Для того чтобы все вершины многогранного множества M (B) при любом целочисленном векторе B были целочисленными, необходимо и достаточно, чтобы каждый минор порядка m матрицы условий [ aij ] был равен либо 0, либо +1 или –1. Если вместо равенств (7.1) множество задается неравенствами, указанные в теореме значения относятся ко всем минорам матрицы [ aij ]. Класс задач, удовлетворяющих теореме, очень узок (это транспортные задачи, задачи о назначениях и др.). Такие задачи относят к лекгоразрешимым (по Дж. Эдмондсу), так как для них существуют полиномиальные алгоритмы (время или число итераций растет полиномиально с увеличением размерности задачи). Остальные целочисленные задачи входят в класс трудноразрешимых задач (класс NP по Карпу и Куку). Для решения таких задач применяются различные подходы. Из точных методов можно назвать следующие: 1. методы отсечений; 2. метод ветвей и границ; 3. метод построения последовательности планов 4. модификации динамического программирования; 5. методы последовательного анализа вариантов. Последние 4 метода входят в группу комбинаторных методов. Кроме точных методов имеется также большое число приближенных методов. Мы остановимся подробнее на первых двух методах как наиболее широко применяемых в пакетах программ, предназначенных для решения задач математического программирования. В ряде из них используются комбинация точных методов, добавление эвристических оценок и другие приемы, позволяющие повысить эффективность алгоритмов. Метод отсечений Идею этого метода высказал Г. Данциг. Она заключается в преобразовании невыпуклого множества целочисленной задачи в выпуклое целочисленное путем отсечения от выпуклого множества непрерывной задачи частей, не содержащих целочисленных точек. Тогда использование методов ЛП гарантирует получение оптимального целочисленного решения (при разрешимости задачи). С этой целью строится выпуклая оболочка допустимого множества целочисленной задачи. Выпуклой оболочкой невыпуклого множества Q называется наименьшее выпуклое множество, содержащее Q. В целочисленной задаче она может быть построена соединением крайних целочисленных точек допустимого множества гиперплоскостями. Пример построения выпуклой оболочки для задачи с двумя переменными показан на рис. 7.2. Здесь соединение крайних точек прямыми позволило получить целочисленное многогранное множество, содержащее все допустимые решения целочисленной задачи. Без требования целочисленности допустимое множество данной задачи представляет собой выпуклый четырехугольник. Как видно, разность этих множеств не содержит целочисленных решений.
Он предложил итерационную процедуру, по которой на каждой итерации отсекается часть множества непрерывной задачи (НЗ), не содержащая целочисленных решений, но включающая оптимальное решение НЗ, и на сокращенном таким способом непрерывном множестве отыскивается новое оптимальное решение одним из методов ЛП. Итерации заканчиваются, когда оптимальное решение очередной НЗ окажется целочисленным или обнаружится неразрешимость НЗ, а значит, и целочисленной задачи. При этом выпуклая оболочка может быть построена только частично.
Проблема состояла в получении регулярного условия, присоединение которого к ограничениям НЗ приводит к необходимому отсечению. Это условие должно удовлетворять двум требованиям: 1) не выполняться в текущем оптимальном решении НЗ; 2) выполняться во всех допустимых целочисленных решениях. Первое требование обеспечит отсечение части непрерывного множества, второе – неизменность целочисленного множества. Гомори предложил несколько вариантов получения условий отсечения. Мы покажем вывод условия отсечения, которое применяется в 1-м алгоритме Гомори. Пусть получено оптимальное решение НЗ. Уравнение, соответствующее строке оптимальной симплекс-таблицы с i- й базисной переменной, записывается следующим образом:
где ai0 – значение базисной переменной Нас интересуют переменные, которые имеют нецелые значения в полученном оптимальном решении. В этих случаях коэффициент ai0 в (7.3), естественно, не целый, а коэффициенты aij могут быть любыми действительными числами. Нецелое значение представим в виде целой и дробной частей. Целая часть числа - наибольшее целое, не превосходящее само число. Будем обозначать ее взятием исходной величины в символы ë×û. Например, ë2.1û=2, ë1.9û=1, ë-2.1û= -3. Применим такое представление к коэффициентам в (7.3). Тогда для дробной части имеем
следовательно, для нецелого aij всегда 0 < Перепишем (7.3) с выделенными целыми и дробными частями коэффициентов:
Оставим в левой части (7.4) только целые части коэффициентов. Тогда, учитывая неотрицательность
Теперь воспользуемся требованием целочисленности. При целых переменных левая часть неравенства (7.5) может принимать только целые значения. Поэтому, если отбросить
(В этом легко убедиться на простых примерах: 9£10.3; 9£9.75). Вычитая (7.6) из равенства (7.3), получаем:
Это и есть искомое условие отсечения. Действительно, в оптимальном решении НЗ (как и в любом базисном) небазисные переменные равны нулю, а
Пример 7.1. Выведем условие отсечения для задачи L= 2 x 1 +x 2 ® max; 15 x 1 + 30 x 2 £ 96; " xj ³ 0, int. Приводим неравенство к каноническому виду 15 x 1 + 30 x 2 + x 3 = 96 и решаем непрерывную задачу симплекс-методом. Получаем оптимальную симплекс-таблицу
Графическое решение показано на рис. 7.4. Записываем уравнение (7.3) по переменной x 1:
При многих нецелых переменных возникает вопрос выбора переменной, по которой следует строить отсечение. Строгого обоснования выбора не имеется. На основе экспериментальных данных рекомендуется брать переменную с наибольшей дробной частью. Второй вопрос относится к способу учета очередного условия отсечения: его можно добавить к условиям исходной задачи и решать задачу заново или после добавления продолжить симплекс-преобразования с полученного оптимального решения, которое стало недопустимым. В алгоритме Гомори применяется второй вариант как более экономичный. Перед добавлением условие отсечения приводится к равенству:
Так как небазисные переменные равны нулю, то новая дополнительная переменная Таким образом, согласно 1-му алгоритму Гомори необходимо выполнить следующие действия. 1. Преобразовать условия задачи так, чтобы все коэффициенты стали целыми. 2. Решить исходную задачу без учета целочисленности (НЗ) одним из методов линейного программирования. Если непрерывная задача неразрешима, то зафиксировать неразрешимость исходной задачи и перейти на 9. 3. Проверить решение на целочисленность: если решение целочисленное, то зафиксировать получение оптимального решения и перейти на 9. 4. Если не все переменные целые, то из оптимальной таблицы выбрать переменную с наибольшей дробной частью. 5. Выписать из симплекс-таблицы строку с выбранной базисной переменной. 6. Выделить дробные части коэффициентов в полученном уравнении и записать условие отсечения согласно (7.7). 7. Привести условие отсечения к равенству (7.8), умножить его на –1 и добавить полученную строку к оптимальной симплекс-таблице. При этом размерность базиса увеличивается на единицу. В качестве недостающей базисной переменной принимается дополнительная переменная из новой строки. 8. Решить расширенную задачу двойственным симплекс-методом. Если задача разрешима, перейти на 3. Иначе зафиксировать неразрешимость целочисленной задачи. 9. Конец. Гомори доказал сходимость этого алгоритма. Примечание. Как следует из алгоритма, на каждой итерации увеличивается размер таблицы (число условий) на единицу. Для ограничения размера используется такой прием. Как только дополнительная переменная какого-либо условия отсечения снова становится базисной (но уже положительной!), строка с ней удаляется из таблицы. Если велся столбец этой переменной, то он тоже удаляется. Подобное исключение не отразится на решении, так как условие удаляется после того, как становится неактивным. В результате число строк не превысит Пример 7.2. Применим приведенный алгоритм к задаче L=2x1+x2®max; 2x1+x2 ³ 7,5; 12x1+7x2£ 55; 5x1+2x2+х5£ 18; x1, x2³ 0, целые. Умножаем 1-е неравенство на 2 и приводим все условия к равенствам: 4x1+2x2-x3 ³ 15; 12x1+7x2+x4 £ 5;5 25x1+10x2+х5£ 90. Решаем непрерывную задачу симплекс-методом. В табл. 7.3 представлено решение НЗ (оптимальная таблица выделена двойной рамкой, строка оценок записана первой для удобства расширения таблицы).
Таблица 7.3 Решение содержит нецелые переменные. Наибольшую дробную часть имеет переменная x3. Выписываем соответствующую ей строку: x3+ которое приводим к равенству - Это равенство добавляем к оптимальной симплекс-таблице решенной НЗ с включением в число базисных вектора А 6 (табл.7.3). К расширенной таблице применяем двойственный метод (направляющей является новая строка, направляющий столбец находится по q). Полученное решение, которое называют оптимальным относительно первого отсечения, приведено в табл. 7.4 (см. часть в двойной рамке).
Оно также является нецелочисленным. Новое отсечение строим по переменной х 2, имеющей наибольшую дробную часть. Выписываем уравнение х 2 +х 4 - из которого следует условие отсечения
и затем равенство
добавляемое к последней симплекс-таблице (см. табл.7.4). Применяем двойственный симплекс-метод. Полученное решение, оптимальное относительно второго отсечения, дано в табл. 7.5. Таблица 7.5
Очевидно, что оно не удовлетворяет требованию целочисленности. Так как в базисное решение вернулась переменная x 6, что означает строгое выполнение 1-го условия отсечения, соответствующие ей строка и столбец удаляются (отмечены выделением пунктирной полосой). Теперь отсечение строим по переменной x 1: х 1- Добавляем полученное уравнение отсечения к последней таблице (табл. 7.5) и, используя снова двойственный метод, находим оптимальное решение расширенной НЗ (табл. 7.6). Это решение целочисленное и, следовательно, оно является оптимальным для исходной целочисленной задачи. ▲
Отмечается зависимость скорости сходимости от формы и порядка записи условий задачи, существенное влияние ошибок округления. Неприятной стороной алгоритма является постоянное увеличение числа строк вплоть до числа переменных в канонической форме. Если задача разрешима, алгоритм находит целочисленное решение только на последней итерации. Поэтому в случае прерывания расчета не будет получено ни одного даже приемлемого решения. Эффективность алгоритма повышается с уменьшением значений аij и bi и заполненности матрицы условий А. Можно рекомендовать применение метода для задач небольшой размерности (до десятков переменных), когда значения аij и bi невелики и в оптимальном решении непрерывной задачи большая часть переменных имеет целые значения. Алгоритм мало пригоден для решения комбинаторных задач в целочисленной постановке. Для других вариантов построения условий отсечения сходимость построенных на них алгоритмов не доказана, а отмеченные недостатки в основном не устраняются. Эти замечания относятся и к алгоритму отсечения для частично целочисленных задач. В ряде пакетов прикладных программ метод отсечений применяется в комбинации с другими, точными или приближенными, методами. Метод ветвей и границ Начало развитию подхода, получившего название метод ветвей и границ, положила работа Ленд и Дойг (1960). Это, скорее, даже не метод, а концепция или процедурная оболочка, на основе которой стали разрабатывать алгоритмы решения целочисленных задач различной природы. Ценность предложенной идеи стала особенно заметна после появления первого точного алгоритма решения задачи коммивояжера, построенного по схеме ветвей и границ (Литтл с соавторами, 1963). Метод можно применять как к полностью, так и частично целочисленным задачам. Суть идеи схожа с известной шуткой о ловле льва в пустыне: делим пустыню пополам; если льва нет в первой половине, ищем во второй, которую делим пополам и т. д. В отличии от льва оптимум не перемещается, и в этом смысле наша задача легче. Метод заключается в построении дерева задач, корнем которого является исходная задача, возможно без условия целочисленности (НЗ). Нижележащие задачи порождаются вышележащими так, что их допустимые множества (ДМ) являются непересекающимися подмножествами ДМ вышележащей задачи. Рост дерева происходит за счет перспективных ветвей. Перспективность определяется по оценке критерия терминальной задачи ветви V и рекорду Z. Оценка V – это значение критерия, заведомо не хуже оптимального, а Z – достигнутое в процессе решения значение критерия исходной задачи (в качестве начального может приниматься значение, заведомо хуже оптимального). Значит, задача будет порождающей только при условии, что ее оценка лучше рекорда. При этом уровень, на котором находится задача, не имеет значения. Рассмотрим метод применительно к линейной целочисленной задаче. Хотя нет каких-либо ограничений на число задач, непосредственно порождаемых перспективной, в алгоритмах, как правило, используется разбиение на две задачи, то есть строится бинарное дерево (рис. 7.5). При этом для целочисленных множеств выполняются соотношения
Вид оценки зависит от направленности критерия: при максимизации используется верхняя оценка, при минимизации – нижняя. Последующее изложение метода будет относиться к задаче на максимум. Для алгоритмической реализации схемы ветвей и границ необходимо решить два основополагающих вопроса: 1. Каким образом разбивать перспективное множество на подмножества; 2. Как определять верхнюю оценку критерия на рассматриваемом множестве. Ответы на них зависят от типа задачи (частично или полностью целочисленная, имеет особые свойства или нет, с булевыми или не булевыми переменными). Ниже рассматривается общий случай. Пусть известен диапазон возможных значений j -й переменной 0 £ хj £ dj, которая в непрерывном оптимальном решении оказалась нецелочисленной и равной xj*. Тогда целочисленное значение этой переменной может достигаться либо в интервале 0 £ хj £
Это соответствует разбиению непрерывного множества Dн на два непересекающихся подмножества D1н и D2н, объединение которых не равно Dн. В то же время такое разбиение целочисленного множества удовлетворяет соотношениям (7.9). При этом целочисленные множества, как исходное, так и порожденные, включены в соответствующие непрерывные множества. Следовательно, поиск целочисленного решения на непрерывном множестве даст тот же результат, что и на целочисленном. Легко увидеть, что приведенное выделение подинтервалов по одной переменной приводит к разбиению исходного множества на два подмножества при любом числе переменных. Теперь перейдем ко второму вопросу. Так как целочисленное множество является подмножеством соответствующего непрерывного, оптимальное значение критерия на непрерывном множестве всегда будет не меньше, чем на целочисленном. Поэтому в качестве верхней оценки V можно брать оптимальное значение критерия L* непрерывной задачи. Выбор начального значения рекорда зависит от ситуации: · если известно какое-либо целочисленное значение, то рекорд принимается равным критерию в этом решении; · при положительности всех коэффициентов критерия можно взять нулевое значение рекорда; · в иных случаях за начальное значение рекорда берется – М, где М- максимально представимое в компьютере число. По ходу разбиения формируются порождаемые задачи, которые помещаются в список задач. Первоначальный список содержит только одну задачу – исходную задачу без условий целочисленности. И в последующем список будет содержать только непрерывные задачи. Таким образом, базовый алгоритм, реализующий метод ветвей и границ, включает следующие шаги. 1. Задается начальное значение рекорда и в список задач помещается исходная задача без требования целочисленности переменных. 2. Анализируется список задач: если он пуст, то переход на шаг 6. Иначе выбирается одна из задач с удалением ее из списка. 3. Выбранная задача решается одним из методов линейного программирования. Если задача неразрешима или оптимальное значение критерия L* £ Z, ветвь обрывается (задача прозондирована). Переход на шаг 2. 4. Полученное решение анализируется на целочисленность. Если решение целочисленное, оно фиксируется, рекорду присваивается оптимальное значение критерия решенной непрерывной задачи (Z:= L*), ветвь обрывается и осуществляется переход на шаг 2. 5. Выбирается одна из переменных, имеющих нецелочисленные значения. По ней производится ветвление: порождаются 2 задачи, одна образуется присоединением к решенной (родительской) задаче условия хj £ 6. Вывод результатов (если значение рекорда больше начального, получено оптимальное решение исходной задачи, иначе задача неразрешима).
Приведенный алгоритм является базовым, так как не включает однозначных правил выбора задачи из списка и ветвящей переменной. Для частично целочисленных задач при выборе переменной для ветвления исключаются непрерывные переменные. Пример 7.3. Применим алгоритм ветвей и границ к задаче L= 9 x 1 + 5 x 2 ® max; 3 x 1 - 6 x 2³1; 5 x 1+2 x 2£ 28; " xj ³ 0, целые. Отбрасывая условие цедочисленности, получаем непрерывную задачу, которую помещаем в список задач. Так как коэффициенты критерия положительны, начальное значение рекорда принимаем равным нулю. Берем из списка единственную задачу и решаем ее. Получаем оптимальное решение в вершине А (рис. 7.7): x 1*=4,72; x 2*=2,19. Ветвление производим по переменной x 1. Добавляя к решенной задаче ограничение x 1£4, образуем задачу 2, а добавление x 1³5 дает задачу 3. Допустимые множества новых задач покзаны на рис. 7.7. Эти задачи помещаем в список задач. Решение задачи 2 достигается в точке В, а задачи 3 – в С. Весь ход решения исходной задачи представлен в виде дерева решений на рис. 7.10. Порядок решения задач из списка отражает счетчик итераций k. На 3-й итерации (задача 4) получено целочисленное решение со значением критерия 41 (точка D на рис. 7.8). Поэтому изменяется рекорд: Z =41. Задача 6 имеет нецелочисленное решение (вершина Е на рис. 7.9), задача 8 – целочисленное решение в точке F. В результате после 7-й итерации рекорд становится равным 50.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 761; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.62 (0.012 с.) |

 , x2= 0.
, x2= 0.
 ; (7.1)
; (7.1) (7.2)
(7.2)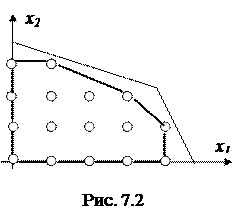 Геометрически все выглядит достаточно просто. Но формализовать процедуру построения целочисленного множества долгое время не удавалось. Первым, кто смог это сделать, был Р. Гомори (1958 г.).
Геометрически все выглядит достаточно просто. Но формализовать процедуру построения целочисленного множества долгое время не удавалось. Первым, кто смог это сделать, был Р. Гомори (1958 г.). Рассмотрим пример (рис. 7.3). Оптимальное решение НЗ как по критерию L 1, так и по L 2находится в вершине A. После первого отсечения нецелочисленной части множества, содержащей точку A, появляется целочисленная вершина B. При решении задачи по критерию L 1 в ней будет оптимум НЗ, а значит, и исходной целочисленной задачи. Если же взять критерий L 2, то оптимум НЗ окажется в вершине C, которая не является целочисленной. Поэтому потребуется еще одно отсечение, после которого будет получено оптимальное целочисленное решение в точке F. В обоих случаях выпуклая оболочка строится только частично.
Рассмотрим пример (рис. 7.3). Оптимальное решение НЗ как по критерию L 1, так и по L 2находится в вершине A. После первого отсечения нецелочисленной части множества, содержащей точку A, появляется целочисленная вершина B. При решении задачи по критерию L 1 в ней будет оптимум НЗ, а значит, и исходной целочисленной задачи. Если же взять критерий L 2, то оптимум НЗ окажется в вершине C, которая не является целочисленной. Поэтому потребуется еще одно отсечение, после которого будет получено оптимальное целочисленное решение в точке F. В обоих случаях выпуклая оболочка строится только частично. , (7.3)
, (7.3) (из столбца А 0), aij – коэффициенты при небазисных переменных (из столбцов А j).
(из столбца А 0), aij – коэффициенты при небазисных переменных (из столбцов А j). ,
, < 1.
< 1. (7.4)
(7.4) и
и  , получаем неравенство
, получаем неравенство
 (7.5)
(7.5) , нестрогое неравенство левой и правой частей сохранится:
, нестрогое неравенство левой и правой частей сохранится: (7.6)
(7.6) . (7.7)
. (7.7)



 x 1 + 2 x 2 +
x 1 + 2 x 2 +  или x 3 ³ 6. Очевидно, что в оптимальном решении НЗ оно не выполняется (х 3 *= 0). Условие отсечения можно записать и через основные переменные. Так как х 3 = 96-15 х 1 - 30 х 2, то 96-15 х 1 - 30 х 2 ³ 6и окончательно имеем х 1 + 2 х 2 £ 6. Граница по этому ограничению показана на рис. 7.4 пунктирной линией. Легко убедиться, что все вершины усеченного множества целочисленные. ▲
или x 3 ³ 6. Очевидно, что в оптимальном решении НЗ оно не выполняется (х 3 *= 0). Условие отсечения можно записать и через основные переменные. Так как х 3 = 96-15 х 1 - 30 х 2, то 96-15 х 1 - 30 х 2 ³ 6и окончательно имеем х 1 + 2 х 2 £ 6. Граница по этому ограничению показана на рис. 7.4 пунктирной линией. Легко убедиться, что все вершины усеченного множества целочисленные. ▲ . (7.8)
. (7.8) . Поэтому рекомендуется для последующего решения применять двойственный симплекс-метод.
. Поэтому рекомендуется для последующего решения применять двойственный симплекс-метод.

 x4+
x4+  x5=
x5=  . Из нее получаем 1-е условие отсечения
. Из нее получаем 1-е условие отсечения  ,
,

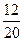









 Базис
Базис



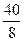


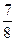



 Из опыта применения рассмотренного алгоритма можно сделать некоторые выводы. Хотя Гомори теоретически доказал, что алгоритм сходится за конечное число шагов, оценки необходимого числа итераций не существует. К сожалению, скорость сходимости алгоритма очень низкая. Встречались примеры с 10-15 переменными, решение которых требовало более тысячи итераций. Попытка вводить отсечение сразу по нескольким переменным не дает ощутимого эффекта.
Из опыта применения рассмотренного алгоритма можно сделать некоторые выводы. Хотя Гомори теоретически доказал, что алгоритм сходится за конечное число шагов, оценки необходимого числа итераций не существует. К сожалению, скорость сходимости алгоритма очень низкая. Встречались примеры с 10-15 переменными, решение которых требовало более тысячи итераций. Попытка вводить отсечение сразу по нескольким переменным не дает ощутимого эффекта. (7.9)
(7.9) Очевидно, что если, например, V 22 окажется хуже рекорда или D 22=Æ, правая ветвь обрывается (говорят также, что она прозондирована). Если же оценка V 22 будет лучше Z,производится ветвление: множество D 22 разбивается на 2 подмножества. Решение завершится, когда все ветвибудут прозондированы.
Очевидно, что если, например, V 22 окажется хуже рекорда или D 22=Æ, правая ветвь обрывается (говорят также, что она прозондирована). Если же оценка V 22 будет лучше Z,производится ветвление: множество D 22 разбивается на 2 подмножества. Решение завершится, когда все ветвибудут прозондированы. , либо в интервале
, либо в интервале  (рис. 7.6).
(рис. 7.6).





