
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача линейного программирования в общем виде.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Симплекс-метод. Симплекс-метод является основным в линейном программировании. Решение задачи начинается с рассмотрений одной из вершин многогранника условий. Если исследуемая вершина не соответствует максимуму (минимуму), то переходят к соседней, увеличивая значение функции цели при решении задачи на максимум и уменьшая при решении задачи на минимум. Таким образом, переход от одной вершины к другой улучшает значение функции цели. Так как число вершин многогранника ограничено, то за конечное число шагов гарантируется нахождение оптимального значения или установление того факта, что задача неразрешима. Этот метод является универсальным, применимым к любой задаче линейного программирования в канонической форме. Система ограничений здесь - система линейных уравнений, в которой количество неизвестных больше количества уравнений. Если ранг системы равен r, то мы можем выбрать r неизвестных, которые выразим через остальные неизвестные. Для определенности предположим, что выбраны первые, идущие подряд, неизвестные x1, x2,..., xr. Тогда наша система уравнений может быть записана как
К такому виду можно привести любую совместную систему, например, методом Гаусса. Правда, не всегда можно выражать через остальные первые r неизвестных (мы это сделали для определенности записи). Однако такие r неизвестных обязательно найдутся. Эти неизвестные (переменные) называются базисными, остальные свободными. Придавая определенные значения свободным переменным и вычисляя значения базисных (выраженных через свободные), мы будем получать различные решения нашей системы ограничений. Таким образом, можно получить любое ее решение. Нас будут интересовать особые решения, получаемые в случае, когда свободные переменные равны нулю. Такие решения называются базисными, их столько же, сколько различных базисных видов у данной системы ограничений. Базисное решение называется допустимым базисным решением или опорным решением, если в нем значения переменных неотрицательны. Если в качестве базисных взяты переменные x1, x2,..., xr, то решение (b1, b 2 ,..., b r, 0,..., 0) будет опорным при условии, что b1, b 2 ,..., b r ≥ 0. Симплекс-метод основан на теореме, которая называется фундаментальной теоремой симплекс-метода: среди оптимальных планов задачи линейного программирования в канонической форме обязательно есть опорное решение ее системы ограничений. Если оптимальный план задачи единственен, то он совпадает с некоторым опорным решением. Различных опорных решений системы ограничений конечное число. Поэтому решение задачи в канонической форме можно было бы искать перебором опорных решений и выбором среди них того, для которого значение Итак, симплексный метод вносит определенный порядок как при нахождении первого (исходного) базисного решения, так и при переходе к другим базисным решениям. Его идея состоит в следующем. Имея систему ограничений, приведенную к общему виду, то есть к системе m линейных уравнений с n переменными (m < n), находят любое базисное решение этой системы, заботясь только о том, чтобы найти его как можно проще. Если первое же найденное базисное решение оказалось допустимым, то проверяют его на оптимальность. Если оно не оптимально, то, осуществляется переход к другому, обязательно допустимому базисному решению. Симплексный метод гарантирует, что при этом новом решении линейная форма, если и не достигнет оптимума, то приблизится к нему. С новым допустимым базисным решением поступают так же, пока не найдут решение, которое является оптимальным. Если первое найденное базисное решение окажется недопустимым, то с помощью симплексного метода осуществляется переход к другим базисным решениям, которые приближают нас к области допустимых решений, пока на каком-то шаге решения либо базисное решение окажется допустимым и к нему применяют алгоритм симплексного метода, либо мы убеждаемся в противоречивости системы ограничений. Таким образом, применение симплексного метода распадается на два этапа: нахождение допустимого базисного решения системы ограничений или установление факта ее несовместности; нахождение оптимального решения. При этом каждый этап может включать несколько шагов, соответствующих тому или иному базисному решению. Но так как число базисных решений всегда ограниченно, то ограниченно и число шагов симплексного метода. Вычисления по симплекс-методу организуются в виде симплекс-таблиц, которые являются сокращенной записью задачи линейного программирования в канонической форме. Перед составлением симплекс-таблицы задача должна быть преобразована, система ограничений приведена к допустимому базисному виду, c помощью которого из целевой функции должны быть исключены базисные переменные. Вопрос об этих предварительных преобразованиях мы рассмотрим ниже. Сейчас же будем считать, что они уже выполнены и задача имеет вид:
Здесь для определенности записи считается, что в качестве базисных переменных можно взять переменные x1, x2,..., xr и что при этом b1, b 2 ,..., b r ≥ 0 (соответствующее базисное решение является опорным). Для составления симплекс-таблицы во всех равенствах в условии задачи члены, содержащие переменные, переносятся в левую часть, свободные оставляются справа, т.е. задача записывается в виде системы равенств:
Далее эта система оформляется в виде симплекс-таблиц: Таблица 34.1
Примечание: Названия базисных переменных здесь взяты лишь для определенности записи и в реальной таблице могут оказаться другими. Шаг 1. Приводим задачу ЛП к каноническому виду с неотрицательными правыми частями
Шаг 2: Строим вспомогательную задачу ЛП
Переменные вспомогательной задачи Вспомогательная задача ЛП всегда имеет решение, причем оптимальное значение целевой функции Приводим вспомогательной задачи ЛП к специальному виду. Для этого целевую функцию выражаем через небазисные переменные.
Шаг 3: Решаем вспомогательную задачу ЛП симплекс-методом. Шаг 4: Если Шаг 5: Если Задача 35.1. Решить задачу линейного программирования
Заметим, что у нас уже есть одна базисная переменная
Итак, у нас получилась вспомогательная задача ЛП:
Исходная симплекс-таблица примет тогда вид:
Дальнейшие итерации приводятся без особых пояснений. Первая итерация Так как из базиса выводится вектор
Вторая итерация На этой итерации из базиса выводится вектор
Третья итерация Мы вернулись к исходной задаче и продолжаем решать ее по стандартной схеме.
Строка целевой функции не содержит положительных значений. Значит, задача решена и оптимальный план имеет вид: (0, 15/7, 25/7, 15/7) Двойственность задач линейного программирования. Таблица соответствий. Определение: двойственная задача – это вспомогательная задача линейного программирования, формулируемая с помощью определенных правил непосредственно из условий исходной задачи, которая в этом случае называется прямой задачей линейного программирования. Таблица 36.1
Трудности в решении задач линейного программирования зависят не от количества переменных n, а от количества ограничений m, определяющих число итераций симплекс-метода. Поэтому, если прямая задача линейного программирования, еще не приведенная к стандартной форме, содержит большое количество ограничений (m>n), то в этом случае целесообразно перейти к двойственной задаче. Сформированная двойственная задача линейного программирования будет иметь m переменных и n ограничений, т.е. количество итераций при этом уменьшится. Рассмотрим пару задач ЛП вида: Таблица 36.2
Задачу (I) называют прямой задачей ЛП, а (II) - двойственной. Ограничения задач (I) и (II), соответствующие друг другу, называются сопряженными. Заметим, что задача двойственная к (II), есть исходная прямая задача, т.е. соотношение двойственности взаимное. Поэтому можно любую из такой пары задач считать прямой, а другую - двойственной. Грубо говоря, двойственная задача - это на 900 повернутая исходная прямая задача. В этой связи полезно усвоить следующую схему соответствия. Задача 36.1: построить двойственную задачу к следующей задаче ЛП:
Прежде чем приступать к построению двойственной задачи, необходимо упорядочить запись исходной: согласовать знаки неравенств в ограничениях задачи с целевой функцией. Так как целевая функция минимизируется, то неравенства должны быть записаны с помощью знака Теперь, вводя двойственные переменные
Таблица 36.3
Итак, задача слева - исходная прямая задача, задача справа - двойственная к исходной задаче.
Теоремы двойственности. Рассмотрим стандартную задачу ЛП и двойственную к ней: Таблица 37.1
Пара двойственных задач (I) и (II) называется парой симметрических двойственных задач. Не ограничивая общности, теорию двойственности можно рассматривать для пары симметрических задач, поскольку для любой задачи ЛП существует эквивалентная ей стандартная задача ЛП и поэтому теоремы, справедливые для пары симметрических двойственных задач, будут справедливы для пары общих двойственных задач. Рассмотрим пару симметрических двойственных задач в матричной форме записи. Таблица 37.2.
Здесь
Основное неравенство двойственности: для любых допустимых решений прямой задачи Следствие (достаточное условие оптимальности): если для некоторых допустимых решений Первая теорема двойственности: е сли одна из пары двойственных задач (I) и (II) разрешима, то разрешима и другая задача, причем оптимальные значения целевых функций прямой и двойственной задач совпадают.
где Вторая теорема двойственности: чтобы допустимые решения 1) 2)
Критерии оптимальности. Первый критерий оптимальности: Решение
Второй критерий оптимальности: чтобы допустимые решения 1) если 2) если 3) если 4) если Пример: используя теоремы двойственности, решить двойственную задачу, если известно решение прямой задачи.
Пусть решение задачи найдено одним из стандартных методов: Построим двойственную задачу:
По первой теореме двойственности задача разрешима, причем
Найдем оптимальный план задачи Получим
Следовательно, неравенство Далее, так как
Получаем систему линейных уравнений:
Планы Рис. 41.1 OABC — область допустимых решений (ОДР). Оптимальное решение задача имеет в точке B (9/5,41/15) при этом максимальное значение целевой функции составляет 218/15 ед. Полученное оптимальное решение не целочисленное. Условию целочисленности переменных удовлетворяют координаты 12 точек, принадлежащих ОДР. Чтобы найти точку, координаты которой определяют решение исходной задачи, заменим многоугольник OABC многоугольником OKEMNF, содержащим все допустимые точки с целочисленными координатами. Строим вектор получим в точке E (1, 3) максимальное значение целевой функции
Ответ: Фирме следует приобрести один комплект оборудования 1-го вида и три комплекта оборудования 2-го вида, что обеспечит ей при имеющихся ограничениях на производственные площади и денежные средства максимальное увеличение выпуска продукции, равное 14 ед. в смену. Метод ветвей и границ.
Пусть
Первоначально находим симплексным методом или методом искусственного базиса оптимальный план задачи без учета целочисленности переменных. Если среди компонент этого плана нет дробных чисел, то тем самым найдено искомое решение данной задачи. Если среди компонент плана имеются дробные числа, то необходимо осуществить переход к новым планам, пока не будет найдено решение задачи. Метод ветвей и границ основан на предположении, что наш оптимальный нецелочисленный план дает значение функции, большее, чем всякий последующий план перехода. Пусть переменная 1. либо меньше или равно ближайшему меньшему целому числу 2. либо больше или равно ближайшему большему целому числу Определяя эти числа, находим симплексным методом решение двух задач:линейного программирования:
и
Возможны четыре случая при решении этой пары задач: 1. Одна из задач неразрешима, а другая имеет целочисленный оптимальный план. Тогда этот план и значение целевой функции дают решение исходной задачи. 2. Одна из задач неразрешима, а другая имеет нецелочисленный оптимальный план. Тогда рассматриваем вторую задачу и в ее оптимальном плане выбираем одну из компонент, значение которой равно дробному числу и строим две задачи, аналогичные предыдущим. 3. Обе задачи разрешимы. Одна из задач имеет оптимальный целочисленный план, а в оптимальном плане другой задачи есть дробные числа. Тогда вычисляем значения целевой функции от планов и сравниваем их между собой. Если на целочисленном оптимальном плане значение целевой функции больше или равно ее значению на плане, среди компонент которого есть дробные числа, то данный целочисленный план является оптимальным для исходной задачи и дает искомое решение. 4. Обе задачи разрешимы, и среди оптимальных планов обеих задач есть дробные числа. Тогда рассматриваем ту из задач, для которой значение целевой функции является наибольшим. И строим две задачи. Алгоритм метода ветвей и границ: 1. Находим решение задачи линейного программирования без учета целочисленности. 2. Составляет дополнительные ограничения на дробную компоненту плана. 3. Находим решение двух задач с ограничениями на компоненту. 4. Строим в случае необходимости дополнительные ограничения, согласно возможным четырем случаям получаем оптимальный целочисленный план либо устанавливаем неразрешимость задачи.
Задача линейного программирования в общем виде. Линейное программирование – это направление математического программирования, изучающее методы решения экстремальных задач, которые характеризуются линейной зависимостью между переменными и линейным критерием. Необходимым условием постановки задачи линейного программирования являются ограничения на наличие ресурсов, величину спроса, производственную мощность предприятия и другие производственные факторы. Сущность линейного программирования состоит в нахождении точек наибольшего или наименьшего значения некоторой функции при определенном наборе ограничений, налагаемых на аргументы и образующих систему ограничений, которая имеет, как правило, бесконечное множество решений. Каждая совокупность значений переменных (аргументов функции F), которые удовлетворяют системе ограничений, называется допустимым планом задачи линейного программирования. Функция F, максимум или минимум которой определяется, называется целевой функцией задачи. Допустимый план, на котором достигается максимум или минимум функции F, называется оптимальным планом задачи. Систе
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 1952; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.36.215 (0.009 с.) |

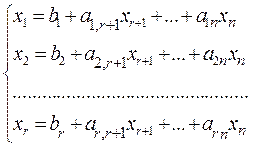 (34.1)
(34.1) самое большое (или самое маленькое). Но, во-первых, все опорные решения неизвестны, и их нужно находить, a, во-вторых, в реальных задачах этих решений очень много и прямой перебор вряд ли возможен. Симплекс-метод представляет собой некоторую процедуру направленного перебора опорных решений. Исходя из некоторого, найденного заранее опорного решения по определенному алгоритму симплекс-метода мы подсчитываем новое опорное решение, на котором значение целевой функции
самое большое (или самое маленькое). Но, во-первых, все опорные решения неизвестны, и их нужно находить, a, во-вторых, в реальных задачах этих решений очень много и прямой перебор вряд ли возможен. Симплекс-метод представляет собой некоторую процедуру направленного перебора опорных решений. Исходя из некоторого, найденного заранее опорного решения по определенному алгоритму симплекс-метода мы подсчитываем новое опорное решение, на котором значение целевой функции 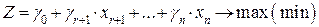
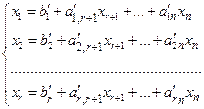 (34.2)
(34.2)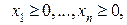
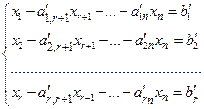 (34.3)
(34.3)
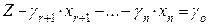


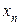
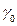

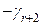
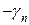



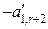
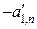

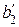
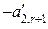
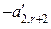

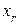
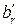
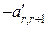
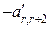
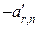
 ,
,  .
.
 (35.1)
(35.1)
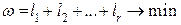
 (35.2)
(35.2) .
. образуют базис вспомогательной задачи ЛП и называются искусственными.
образуют базис вспомогательной задачи ЛП и называются искусственными.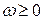
 (35.3)
(35.3) , то допустимого решения в исходной задаче не существует. Задача не разрешима и процесс решения исходной задачи завершается.
, то допустимого решения в исходной задаче не существует. Задача не разрешима и процесс решения исходной задачи завершается. , то приводим исходную задачу к виду (35.1) на основе оптимальной симплек-таблицы вспомогательной задачи ЛП. Подготовительный этап симплекс-метода исходной задачи на этом завершается.
, то приводим исходную задачу к виду (35.1) на основе оптимальной симплек-таблицы вспомогательной задачи ЛП. Подготовительный этап симплекс-метода исходной задачи на этом завершается.


 . Поэтому вводим лишь две искусственные переменные
. Поэтому вводим лишь две искусственные переменные  и
и  , заменяя исходную задачу следующей:
, заменяя исходную задачу следующей:






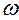





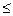 (этот знак неравенства согласован с целевой функцией на максимум)
(этот знак неравенства согласован с целевой функцией на максимум)

 , не имеющая ограничения в знаке
, не имеющая ограничения в знаке

 (этот знак неравенства согласован с целевой функцией на минимум)
(этот знак неравенства согласован с целевой функцией на минимум)
 , не имеющая ограничения в знаке
, не имеющая ограничения в знаке
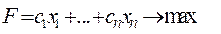
 ………………………
………………………
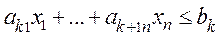



 ………
………

 - любое
……..
- любое
……..
 - любое
- любое

 ………
………
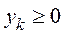
 - любое
……..
- любое
……..
 - любое
- любое
 ……………………………..
……………………………..
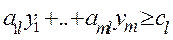





 Для этого второе неравенство умножим на -1:
Для этого второе неравенство умножим на -1: 
 ,
,  ,
,  , запишем в соответствии с указанным правилом пару двойственных задач:
, запишем в соответствии с указанным правилом пару двойственных задач:




 - любое
- любое
 - любое
- любое

 - любое
- любое







 ………………………
………………………




 ……………………………..
……………………………..







 ,
, 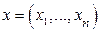 ,
, 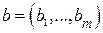 ,
,  ,
, - матрица из
- матрица из  строк и
строк и  столбцов,
столбцов,  - транспонированная матрица. Введем обозначения для допустимых областей задачи (I) и (II).
- транспонированная матрица. Введем обозначения для допустимых областей задачи (I) и (II). ,
, 
 и для любых допустимых решений двойственной задачи
и для любых допустимых решений двойственной задачи 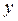 выполняется неравенство
выполняется неравенство  .
.  и
и  выполняется равенство значений целевых функций
выполняется равенство значений целевых функций  , то
, то  ,
,  - оптимальные решения задачи (I) и (II) соответственно.
- оптимальные решения задачи (I) и (II) соответственно. , (37.1)
, (37.1) ,
,  оптимальные планы задач (I) и (II) соответственно.
оптимальные планы задач (I) и (II) соответственно. ,
,  пары двойственных задач (I) и (II) были оптимальными необходимо и достаточно, чтобы выполнялись условия:
пары двойственных задач (I) и (II) были оптимальными необходимо и достаточно, чтобы выполнялись условия: , (37.2)
, (37.2) . (37.3)
. (37.3)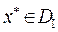 оптимально тогда и только тогда, когда существует решение
оптимально тогда и только тогда, когда существует решение  такое, что
такое, что . (38.1)
. (38.1) , то
, то 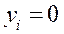 ; (38.2)
; (38.2) , то
, то  ; (38.3)
; (38.3) , то
, то  ; (38.4)
; (38.4)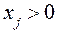 , то
, то  . (38.5)
. (38.5)
 , (38.6)
, (38.6) ,
,  ,
,  .
. ,
,  .
.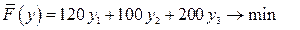
 , (38.7)
, (38.7) ,
,  ,
,  .
. .
. , используя вторую теорему двойственности. Подставим координаты вектора
, используя вторую теорему двойственности. Подставим координаты вектора  в ограничения задачи (38.6).
в ограничения задачи (38.6).


 должно выполняться как равенство, то есть
должно выполняться как равенство, то есть  .
. ,
,  , то
, то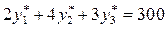 ,
,  .
. ,
,  ,
, 
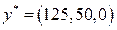 , в силу второй теоремы двойственности, являются оптимальными в задачах (38.6) и (38.7) соответственно.
, в силу второй теоремы двойственности, являются оптимальными в задачах (38.6) и (38.7) соответственно. . Линию уровня перемещаем по направлению
. Линию уровня перемещаем по направлению  ,
, (ед.)
(ед.) (43.1)
(43.1) ,
,  , (43.2)
, (43.2) ,
,  - целые,
- целые,  . (43.3)
. (43.3) в плане – дробное число. Тогда в оптимальном плане ее значение будет, по крайней мере:
в плане – дробное число. Тогда в оптимальном плане ее значение будет, по крайней мере: ;
; .
. (43.4)
(43.4) (43.6)
(43.6) ,
,  - целые,
- целые,  . (43.7)
. (43.7) , (43.9)
, (43.9) (43.10)
(43.10) - целые,
- целые, 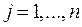 . (43.11)
. (43.11)


