
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основная задача линейного программированияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Любую задачу линейного программирования можно свести к стандартной форме, так называемой «основной задаче линейного программирования» (ОЗЛП), которая формулируется так: найти неотрицательные значения переменных х1, х2,..., xn, которые удовлетворяли бы условиям-равенствам
и обращали бы в максимум линейную функцию этих переменных:
L = c1x1 + c2x2 +... + cnxn =>max. (8.2)
Убедимся в этом. Uo-нерпых, случай, когда L надо обратить не в максимум, а и минимум, легко сводится к предыдущему, если попросту изменить знак L на обратный (максимизировать не L, а L' = — L). Кроме того, от любых условий-неравенств можно перейти к условиям-равенствам ценой введения некоторых новых «дополнительных» переменных. Покажем, как это делается, на конкретном примере. Пусть требуется найти неотрицательные значения переменных х1, х2, х3, удовлетворяющие ограничениям-неравенствам
и обращающие в максимум линейную функцию от этих переменных:
L = 4х1 – х2 + 2х3 => max. (8.4)
Начнем с того, что приведем условия (8.3) к стандартной форме, так, чтобы знак неравенства был
А теперь обозначим левые части неравенств (8.5) соответственно через у1 и у2:
Из условий (8.5) и (8.6) видно, что новые переменные у1, у2 также должны быть неотрицательными. Какая же теперь перед нами стоит задача? Найти неотрицательные значения переменных х1, х2, х3, y1, у2 такие, чтобы они удовлетворяли условиям-равенствам (8.6) и обращали в максимум линейную функцию этих переменных (то, что в L не входят дополнительные переменные у1, у2, неважно: можно считать, что они входят, но с нулевыми коэффициентами). Перед нами — основная задача линейного программирования (ОЗЛП). Переход к ней от первоначальной задачи с ограничениями-неравенствами (8.3) «куплен» ценой увеличения числа переменных на два (число неравенств). Возможен и обратный переход: от ОЗЛП к задаче с ограничениями-неравенствами. Пусть перед нами основная задача линейного программирования с ограничениями-равенствами (8.1). Предположим, что среди этих т равенств линейно независимыми являются r
Итак, всякая задача линейного программирования может быть сведена к стандартной форме ОЗЛП. Мы не будем подробно останавливаться на способах решения этой задачи. Им посвящены специальные руководства (например, [4, 5]), они описаны во многих книгах по исследованию операций (например, [6, 7]). В следующем параграфе мы изложим только некоторые соображения общего характера относительно существования решения ОЗЛП и способов его нахождения. Никакими расчетными алгоритмами мы заниматься не будем, а отошлем интересующегося читателя к вышеупомянутым руководствам.
1) Равенства называются линейно независимыми, если никакое из них нельзя получить из других путем умножения на какие-то коэффициенты и суммирования, т. е. никакое из них не является следствием остальных.)
|
|||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 787; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.239.215 (0.008 с.) |

 (8.1)
(8.1) (8.3)
(8.3)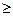 , а справа стоял нуль. Получим:
, а справа стоял нуль. Получим: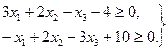 (8.5)
(8.5) (8.6)
(8.6) т 1). В линейной алгебре доказывается (см., например, [4]), что максимальное число линейно независимых равенств, связывающих п переменных x1, x2,..., xn, равно п, так что вообще r
т 1). В линейной алгебре доказывается (см., например, [4]), что максимальное число линейно независимых равенств, связывающих п переменных x1, x2,..., xn, равно п, так что вообще r 


