
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сведение матричных игр к задаче линейного программирования.Содержание книги
Поиск на нашем сайте
Рассмотрим сведение матричной игры к задаче линейного программирования. Пусть игра задана платежной матрицей
Цель игрока А: На практике задачу еще упрощают. Все неравенства можно разделить на n > 0 и ввести новые переменные Найти значения переменных
и обращают в минимум целевую функцию: Как было отмечено, решается задача симплексным методом. Аналогично, составляется задача линейного программирования для игрока В (двойственная по отношению к задаче для игрока А): Найти значения переменных
и обращают в минимум целевую функцию: По найденным значениям переменных находят цену игры и компоненты смешанных стратегий игроков. Если матрицу предварительно преобразовывали, то в конце цену игры необходимо уменьшить на значение g. Значение цены игры является общим для обоих игроков. В некоторых случаях используют приближенные методы решения матричных игр, например, метод фиктивного разыгрывания (метод Брауна-Робинсон).
Понятие о динамическом программировании. Динамическое программирование в математике и теории вычислительных систем — способ решения сложных задач путём разбиения их на более простые подзадачи. Он применим к задачам с оптимальной подструктурой, выглядящим как набор перекрывающихся подзадач, сложность которых чуть меньше исходной. В этом случае время вычислений, по сравнению с «наивными» методами, можно значительно сократить. Ключевая идея в динамическом программировании достаточно проста. Как правило, чтобы решить поставленную задачу, требуется решить отдельные части задачи (подзадачи), после чего объединить решения подзадач в одно общее решение. Часто многие из этих подзадач одинаковы. Подход динамического программирования состоит в том, чтобы решить каждую подзадачу только один раз, сократив тем самым количество вычислений. Это особенно полезно в случаях, когда число повторяющихся подзадач экспоненциально велико.
Метод динамического программирования сверху — это простое запоминание результатов решения тех подзадач, которые могут повторно встретиться в дальнейшем. Динамическое программирование снизу включает в себя переформулирование сложной задачи в виде рекурсивной последовательности более простых подзадач. Динамическое программирование обычно применяется к задачам, в которых искомый ответ состоит из частей, каждая из которых в свою очередь дает оптимальное решение некоторой подзадачи. Динамическое программирование полезно, если на разных путях многократно встречаются одни и те же подзадачи; основной технический приём — запоминать решения встречающихся подзадач на случай, если та же подзадача встретится вновь. В типичном случае динамическое программирование применяется к задачам оптимизации. У такой задачи может быть много возможных решений, но требуется выбрать оптимальное решение, при котором значение некоторого параметра будет минимальным или максимальным. Типовой алгоритм решения задач методом динамического программирования: 1. Описать строение оптимальных решений. 2. Выписать рекуррентное соотношение, связывающие оптимальные значения параметра для подзадач. 3. Двигаясь снизу вверх, вычислить оптимальное значение параметра для подзадач. 4. Пользуясь полученной информацией, построить оптимальное решение.
Принцип Беллмана. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ — раздел математического программирования, совокупность приемов, позволяющих находить оптимальные решения, основанные на вычислении последствий каждого решения и выработке оптимальной стратегии для последующих решений. Процессы принятия решений, которые строятся по такому принципу, называются многошаговыми процессами. БЕЛЛМАНА ПРИНЦИП ОПТИМАЛЬНОСТИ — важнейшее положение динамического программирования, которое гласит: оптимальное поведение в задачах динамического программирования обладает тем свойством, что каковы бы ни были первоначальное состояние и решение (т. е. “управление”), последующие решения должны составлять оптимальное поведение относительно состояния, получающегося в результате первого решения. Этот принцип можно выразить и рассуждая от противного: если не использовать наилучшим образом то, чем мы располагаем сейчас, то и в дальнейшем не удастся наилучшим образом распорядиться тем, что мы могли бы иметь.
Принцип Беллмана дает достаточные условия оптимальности процесса в задаче оптимального управления. Он базируется на следующем ключевом факте: Если кривая x*(t) является оптимальной траекторией в задаче управления динамической системой на отрезке времени [t0, T], с некоторым начальным условием x(t0) = x0, то для любого момента времени t Î [t0, T] оптимальным решением задачи управления системой на отрезке времени [t, T] с начальным условием x(t) = x*(t) будет являться участок той же самой траектории x*(t) Следовательно, если имеется оптимальная траектория, то и любой ее участок представляет собой оптимальную траекторию. Этот принцип позволяет сформулировать эффективный метод решения широкого класса многошаговых задач. Принцип назван по имени крупного американского математика Р. Беллмана, одного из основоположников динамического программирования.
|
||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 335; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.249.240 (0.009 с.) |

 . Игроку А необходимо найти такую смешанную стратегию
. Игроку А необходимо найти такую смешанную стратегию  , что при любом поведении игрока В он получит выигрыш не меньше некоторого числа n. Этому утверждению соответствует следующая система неравенств:
, что при любом поведении игрока В он получит выигрыш не меньше некоторого числа n. Этому утверждению соответствует следующая система неравенств:
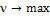 . В такой постановке получили задачу линейного программирования с переменными
. В такой постановке получили задачу линейного программирования с переменными  , причем все переменные неотрицательны (
, причем все переменные неотрицательны ( как вероятность, считаем n > 0). Значит, эту задачу можно решить симплексным методом.
как вероятность, считаем n > 0). Значит, эту задачу можно решить симплексным методом. . С учетом равенства
. С учетом равенства  рассматривают функцию
рассматривают функцию  . Т.к.
. Т.к.  . Получаем задачу линейного программирования (для игрока А):
. Получаем задачу линейного программирования (для игрока А): , которые удовлетворяют системе ограничений:
, которые удовлетворяют системе ограничений:

 , которые удовлетворяют системе ограничений:
, которые удовлетворяют системе ограничений:




