Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Игры с полной/неполной информациейСодержание книги
Поиск на нашем сайте В играх с полной информацией описание игры известно всем игрокам (все игроки знают чистые стратегии и функции полезности всех остальных игроков). В играх с неполной информацией некоторые игроки могут не знать функции полезности других игроков (то есть не знать некоторые конкретные значения для ячеек таблицы из нашего примера). Любая игра в экстенсивной форме может быть представлена игрой в нормальной форме (не обязательно эквивалентной). Представление игры в нормальной форме может быть использовано для нахождения доминируемых стратегий. Формальное представление
У каждого игрока
Исход игры — это комбинация чистых стратегий каждого игрока:
где
Функция полезности i -го игрока (функция платежа):
Def.: В нормальной форме игра представляется как множество:
где:
Решение матричных игр: доминирование строк и столбцов. Матричную игру можно упростить, выявив доминирование одних стратегий над другими. Рассмотрим такую ситуацию. Для игры с платёжной матрицей Стратегия Если для той же матричной игры рассмотреть две стратегии игрока В - то стратегия Если в платёжной матрице есть одинаковые строки (столбцы), то соответствующие стратегии игрока А (игрока В) называются дублирующими. В матричной игре доминируемые и дублирующие стратегии называются излишними, поэтому их можно опускать, упрощая тем самым матричную игру. Для этого в платёжной матрице вычёркивают строки или столбцы, соответствующие излишним стратегиям игроков. 45. Решение матричных игр: аффинные преобразования. Определение. Преобразование плоскости называется аффинным, если · оно взаимно однозначно; · образом любой прямой является прямая. Преобразование называется взаимно однозначным, если · разные точки переходят в разные; · в каждую точку переходит какая-то точка. Однородные координаты Определение. Однородные координаты — координаты, обладающие тем свойством, что определяемый ими объект не меняется при умножении всех координат на одно и то же число. Однородными координатами вектора (х, у) является тройка чисел (x', y', h), где х = х' / h, у = y'/h, а h — некоторое вещественное число (случай, когда h = 0 является особым). Прим. Данные координаты не позволяют однозначно задать точку плоскости. Например, (1, 1, 1) и (2, 2, 2) задают одну и ту же точку (1, 1). Предлагается взять набор (x, y, 1), который будет описывать все точки плоскости. Матрица преобразования для однородных координат имеет размер 3х3. Рассмотрим некоторые преобразования в однородных координатах. Сжатие/растяжение
Это преобразование умножает соответствующие координаты точек на коэффициенты масштабирования по осям: (x, y) -> (ax * x, ay * y). Матрица преобразования запишется следующим образом: [ ax 0 0 ] [ 0 ay 0 ] [ 0 0 1 ] Где ax – растяжение по оси x, ay – растяжение по оси y. Прим. Можно заметить, что при отрицательных значениях коэффициентов сжатия/растяжения происходит отражение относительно соответствующих осей. Этот случай можно включить в данное преобразование, а можно вынести в отдельное, сказав, что коэффициенты масштабирования принимают только положительные значения. Поворот
Матрица поворота 2x2 была подробно разобрана ранее. Теперь она дополняется строкой и столбцом: [ cos(phi) sin(phi) 0 ] [ -sin(phi) cos(phi) 0 ] [ 0 0 1 ] Прим. При угле phi = п эта матрица задает центральную симметрию относительно начала координат, которая является частным случаем поворота. Можно заметить, что такую симметрию можно задать с помощью преобразования сжатия/растяжения (допуская отрицательные коэффициенты масштабирования). Параллельный перенос
Исходный вектор (x, y) переходит в (x + tx, y + ty). Матрица преобразования запишется следующим образом: [ 1 0 0 ] [ 0 1 0 ] [ tx ty 1 ] Отражение
Как говорилось в примечании к преобразованию сжатия/растяжения, отражения получаются следующим образом: [ -1 0 0 ] [ 0 1 0 ] [ 0 0 1 ] [ 1 0 0 ] [ 0 -1 0 ] [ 0 0 1 ] Общий вид аффинного преобразования Матрица 3x3, последний столбец которой равен (0 0 1)T, задает аффинное преобразование плоскости: [ * * 0 ] [ * * 0 ] [ * * 1 ] По одному из свойств, аффинное преобразование можно записать в виде: f(x) = x * R + t, где R – обратимая матрица 2x2, а t – произвольный вектор. В однородных координатах это запишется следующим образом: [ R1,1 R1,2 0 ] [ R2,1 R2,2 0 ] [ tx ty 1 ] Если умножить вектор-строку на эту матрицу получаем результат преобразования: [ x y 1 ] * [ R1,1 R1,2 0 ] [ R2,1 R2,2 0 ] [ tx ty 1 ] = [ x’ y’ 1 ] + [ tx ty 1 ] При этом [ x’ y’ ] = R * [ x y ] Прим. При аффинном преобразовании площади всех фигур изменяются в |R|. Т.о. аффинное преобразование представляется в виде композиции некоторого преобразования, задаваемого матрицей R, и параллельного переноса. Матрица R определяет новый базис плоскости. Т.е. вектор (1, 0) переходит в (R1,1, R1,2), вектор (0, 1) переходит в (R2,1, R2,2). Новый базис это строки матрицы R. Пример.
При отражении относительно оси y, базисный вектор по оси ординат сохраняется, а по оси абсцисс переходит в (-1, 0). Т.о. матрица R будет выглядеть следующим образом: [ -1 0 ] [ 0 1 ] Теперь становится ясно, что кроме вышеперечисленных преобразований, с помощью аффинного преобразования можно получить скос:
|
||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 438; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.170 (0.009 с.) |

 — множество игроков
— множество игроков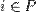 имеется конечный набор чистых стратегий Si
имеется конечный набор чистых стратегий Si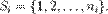



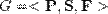
 — множество множеств чистых стратегий каждого игрока,
— множество множеств чистых стратегий каждого игрока, — множество функций платежей для каждого игрока
— множество функций платежей для каждого игрока рассмотрим две стратегии игрока А –
рассмотрим две стратегии игрока А –  и
и  такие, что
такие, что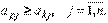
 называется доминирующей, а стратегия
называется доминирующей, а стратегия  − доминируемой.
− доминируемой. и
и  такие, что
такие, что
 называется доминирующей, а стратегия
называется доминирующей, а стратегия  − доминиру-емой.
− доминиру-емой.