
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общая и типовая задача в линейном программировании.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Оптимизационная задача - это экономико-математическая задача, которая состоит в нахождении оптимального (максимального или минимального) значения целевой функции, причем значения переменных должны принадлежать некоторой области допустимых значений. В самом общем виде задача математически записывается так: U = f(X) max; X W, Где X = (Х1, Х2,…, Хn); W - область допустимых значений переменных Х1, Х2,…, Хn; f(X) - целевая функция. Для того, чтобы решить задачу оптимизации, достаточно найти ее оптимальное решение, т.е. указать X() W такое, что f(X()) f(X), при любом X W, или для случая минимизации - что f(X())? f(X), при любом X W. Оптимизационная задача является неразрешимой, если она не имеет оптимального решения. В частности, задача максимизации будет неразрешима, если целевая функция f(X) не ограничена сверху на допустимом множестве W. Методы решения оптимизационных задач зависят как от вида целевой функции f(X), так и от строения допустимого множества W. Если целевая функция в задаче является функцией n переменных, то методы решения называют методами математического программирования. В математическом программировании принято выделять следующие основные задачи в зависимости от вида целевой функции f(X) и от области W: · задачи линейного программирования, если f(X) и W линейны; · задачи целочисленного программирования, если ставится условие целочисленности переменных Х1, Х2,…, Хn; · задачи нелинейного программирования, если форма f(X) носит нелинейный характер. Задачи линейного программирования. Задачей линейного программирования называется задача исследования операций, математическая модель которой имеет вид: f(X) = СjXj max(min); aij xj = bi, iI, IM = 1, 2,…m; aij xj bi, iM; Xj0, jJ, JN = 1, 2,…n. При этом система линейных уравнений и неравенств, определяющая допустимое множество решений задачи W, называется системой ограничений задачи линейного программирования, а линейная функция f(X) называется целевой функцией или критерием оптимальности. Любую задачу линейного программирования можно свести к задаче линейного программирования в канонической форме. Для этого в общем случае нужно уметь сводить задачу максимизации к задаче минимизации; переходить от ограничений неравенств к ограничениям равенств и заменять переменные, которые не подчиняются условию неотрицательности. Максимизация некоторой функции эквивалентна минимизации той же функции, взятой с противоположным знаком, и наоборот. Правило приведения задачи линейного программирования к каноническому виду состоит в следующем: 1) если в исходной задаче требуется определить максимум линейной функции, то следует изменить знак и искать минимум этой функции; 2) если в ограничениях правая часть отрицательна, то следует умножить это ограничение на -1; 3) если среди ограничений имеются неравенства, то путем введения дополнительных неотрицательных переменных они преобразуются в равенства; 4) если некоторая переменная Хk не имеет ограничений по знаку, то она заменяется (в целевой функции и во всех ограничениях) разностью между двумя новыми неотрицательными переменными:: Xk = X`k - Xl, где l - свободный индекс, X`k 0, Xk 0.
8, 1. Каждому опорному/базисному решению ЗЛП соответствует крайняя угловая точка выпуклого многогранника D, представляющего собой область допустимых решений задачи (*),и наоборот. 2. Целевая функция z ЗЛП (*) достигает своего оптимума в крайней точке выпуклого многогранника D, порожденного условиями задачи (*). Если целевая функция z ЗЛП (*) достигает своего оптимума более чем в одной крайней точке выпуклого многогранника D, порожденного условиями задачи (*), то она достигает своего оптимума в любой точке, являющейся выпуклой комбинацией данных крайних точек. Линейное программирование — раздел математического программирования, применяемый при разработке методов отыскания экстремума линейных функций нескольких переменных при линейных дополнительных ограничениях, налагаемых на переменные. По типу решаемых задач его методы разделяются на универсальные и специальные. С помощью универсальных методов могут решаться любые задачи линейного программирования (ЗЛП). Специальные методы учитывают особенности модели задачи, ее целевой функции и системы ограничений. Теорема. Если система векторов 9, Для более полного представления о задаче линейного программирования сделаем её геометрическую интерпретацию. Совокупность любого числа линейных ограничений выделяет в пространстве x1, x1,..., xn некоторый выпуклый многогранник, ограничивающий область допустимых значений переменных (ОДЗП). Геометрическую интерпретацию и решение задачи линейного программированиянетрудно получить лишь в простейших случаях при n = 2 или n = 3. Рассмотрим задачу: max{F(x)= c1x1+ c2x2|(aj1x1+ aj2x2)≥(≤)bj,j=1,m; x1≥0, x2≥0}. Каждое из ограничивающих неравенств определяет полуплоскость, лежащую по одну сторону прямой a aj1x1+ aj2x2)=bj, j = 1,m. ОДЗП получится в результате пересечения m полуплоскостей. Условия неотрицательности позволяют ограничиться рассмотрением положительного квадранта.На рис. 1 показан один из возможных вариантов ОДЗП в виде замкнутого многоугольника для случая m = 3. Рисунок 1 - Графическая интерпретация задачи линейного программирования Координаты x1 и x2 любой точки, принадлежащей области, удовлетворяют системе ограничений задачи линейного программирования. Чтобы найти оптимальное решение, зададим функции цели некоторое постоянное значение F1 = c1x1 + c2x2 = const и построим прямую F1, которая будет отсекать на оси ординат (x1 = 0) отрезок, x2=F1/c2 а на оси абсцисс (x2=0) – отрезок x1=F1/c1. Если задать другие значения функции цели F2, F3,... и изобразить соответствующие линии, то получим семейство параллельных прямых, которые называются линиями уровня функции цели. Направление стрелки показывает направление увеличения целевой функции F1 < F2 < F3 <.... Величину функции цели можно характеризовать расстоянием d от начала координат до линии уровня в соответствии с выражением d=(F1/F2)cosα. В теории линейного программирования доказано, что если оптимальное решение задачи линейного программирования существует и единственно, то оно достигается в некоторой вершине многоугольника решений. Очевидно, что целевая функция достигает максимального значения тогда, когда её линия будет проходить через точку M. Координаты этой точки будут оптимальным решением задачи. Минимальное значение рассматриваемой функции будет достигаться в начале координат. Таким образом, если требуется определить такие x1 и x2, которые обеспечивают максимум функции цели, то геометрически это означает, что необходимо провести прямую F = const, проходящую хотя бы через одну вершину области и имеющую максимальное расстояние d от начала координат. В случае минимизации это расстояние должно быть минимальным. В зависимости от вида ОДЗП и расположения линий уровня могут встретиться случаи, изображенные на рис. 2.
Рис. 2 - Различные варианты решения задач линейного программирования На рис.2, а функция F достигает минимума в начале координат. При максимизации функции ее линия совпадает со стороной ВС, ограничивающей ОДЗП. Координаты любой точки отрезка ВС будут доставлять максимум функции F, что соответствует бесчисленному множеству оптимальных решений задачи линейного программирования. На рис. 2, б ОДЗП не замкнута, целевая функция сверху не ограничена, т.е. максимального значения не имеет. Минимальное значение функция принимает в точке A. На рис. 2, в приведен случай несовместных ограничений, в этом случае функция цели не имеет ни максимума, ни минимума, так как ОДЗП представляет собой пустое множество.
10.Графический метод основан на геометрической интерпретации задачи линейного программирования и применяется в основном при решении задач двумерного пространства и только некоторых задач трёхмерного пространства, так как довольно трудно построить многогранник решений, который образуется в результате пересечения полупространств. Задачу пространства размерности больше трёх изобразить графически вообще невозможно. Пусть задача линейного программирования задана в двумерном пространстве, то есть ограничения содержат две переменные. Найти минимальное значение функции
При (2): a11x1+a22x2<= b1, a21x1+a22x2<=b2 X1,x2>0 Допустим, что система (2) при условии (3) совместна и её многоугольник решений ограничен. Каждое из неравенств (2) и (3), как отмечалось выше, определяет полуплоскость с граничными прямыми: Значения
Случай 1. Прямая Случай 2. Прямая, передвигаясь, всё же становится опорной относительно многоугольника решений. Тогда в зависимости от вида области линейная функция может быть ограниченной сверху и неограниченной снизу, ограниченной снизу и неограниченной сверху, либо ограниченной как снизу, так и сверху.
11. Построение опорных планов в симплексном методе решения ЗДП. Симплексный метод – это метод целенаправленного перебора опорных решений задачи. Этот метод позволяет за конечное число шагов расчёта найти оптимальное решение либо установить, что решения не существует. Содержание метода: 1)указать способ нахождения начального опорного решения; 2)указать способ перехода то одного опорного решения к другому, на котором значение целевой функции ближе к оптимальному; 3)задать критерий, который позволяет прекратить перебор решений на оптималном решении или сделать заключение об отсутствии решения. Пусть имеется задача в канонической форме: Z(x)=C1x1+C2x2+…+Cnxn → max (min) a11x1+a12x2+…+a1nxn=b1 a21x1+a22x2+…+a2nxn=b2 ... am1x1+am2x2+…+amnxn=bm xj≥0; j=1…n bi≥0; i=1…m Замечание. Если какая-либо правая часть отрицательная, то это уравнение нужно умножить на -1. Любую задачу можно представить в векторной форме. АХ=В, где Решение, удовлетворяющее всем ограничениям и условиям неотрицательности, называется допустимым. Множество всех допустимых решений образуют область допустимых решений (ОДР). Допустимое решение, доставляющее мин. или макс. целевой функции называется оптимальным решением. Матрица А, составленная из коэффициентов при неизвестных называется матрицей условий. Вектор столбец А0=
Замечание. Нахождение оптимального решения может вызвать затруднение с перебором всех опорных решений когда задача имеет бесконечное множество решений или решение отсутствует. По этому вводят специальный параметр θ. Построение начального опорного решения. Необходимо в каждом уравнении системы найти базисную переменную (которая входит только в одно уравнение с коэффициентом +1). Обозначаю базисную переменную хiб. х1б – базисная переменная первого уравнения и т.д. Составляется первая симплекс-таблица следующим образом.
Где Сiб коэффициент из целевой функции при соответствующей базисной переменной. xjб – базисная переменная из соответствующего уравнения. bi – свободные члены системы. В верхнюю строчку над х выписывают все коэффициенты из целевой функции. Последнюю строчку называют проверочной. Элементы, входящие в эту строку называются оценками переменных. Столбец А0 в результате показывает значение целевой функции начального опорного решения.
Критерий оптимальности Проверка на оптимальность опорного плана проходит с помощью критерия оптимальности, переход к другому опорному плану — с помощью преобразований Жордана-Гаусса и с использованием критерия оптимальности. Полученный опорный план снова проверяется на оптимальность и т.д. Процесс заканчивается за конечное число шагов, причем на последнем шаге либо выявляется неразрешимость задачи (конечного оптимума нет), либо получаются оптимальный опорный план и соответствующее ему оптимальное значение целевой функции. Признак оптимальности заключается в следующих двух теоремах. Теорема 1. Если для некоторого вектора, не входящего в базис, выполняется условие:
то можно получить новый опорный план, для которого значение целевой функции будет больше исходного; при этом могут быть два случая: если все координаты вектора, подлежащего вводу в базис, неположительны, то задача линейного программирования не имеет решения; если имеется хотя бы одна положительная координата у вектора, подлежащего вводу в базис, то можно получить новый опорный план. Теорема 2. Если для всех векторов выполняется условие
13. алгоритм стандартного симплекс методоа
14. Рассматривая симплекс-метод, мы предполагали, что задача линейного программирования является невырожденной, т.е. каждый опорный план содержит ровно m положительных компонент, где m - число ограничений в задаче. В вырожденном опорном плане число положительных компонент оказывается меньше числа ограничений: некоторые базисные переменные, соответствующие данному опорному плану, принимают нулевые значения. Используя геометрическую интерпретацию для простейшего случая, когда n - m = 2 (число небазисных переменных равно 2), легко отличить вырожденную задачу от невырожденной. В вырожденной задаче в одной вершине многогранника условий пересекается более двух прямых, описываемых уравнениями вида xi = 0. Это значит, что одна или несколько сторон многоугольника условий стягиваются в точку. Опорный план называется невырожденным, если он содержит ровно т положительных компонент, в противном случае он называется вырожденным. Если при соблюдении условия допустимости для исключения из базиса можно выбрать более чем 1 вариант, то следующая итерация симплекс метода приведёт к вырожденному решению, когда одна из базисных переменных равна нулю. Последующие итерации могут не привести к улучшению значений целевой функции и становится возможным бесконечное повторение одной и той же последовательности итераций, не улучшающих решение. Такая ситуация называется зацикливанием. Чтобы обеспечивать единственность выбора выводимого вектора, исходя из условий допустимости, разработано несколько специальных приёмов.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 967; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.009 с.) |

 содержит m линейно независимых векторов
содержит m линейно независимых векторов  , то допустимый план
, то допустимый план  (2. 10)
(2. 10)

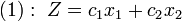
 . Линейная функция (1) при фиксированных значениях
. Линейная функция (1) при фиксированных значениях  является уравнением прямой линии:
является уравнением прямой линии:  . Построим многоугольник решений системы ограничений (2) и график линейной функции (1) при
. Построим многоугольник решений системы ограничений (2) и график линейной функции (1) при  . Тогда поставленной задаче линейного программирования можно дать следующую интерпретацию. Найти точку многоугольника решений, в которой прямая
. Тогда поставленной задаче линейного программирования можно дать следующую интерпретацию. Найти точку многоугольника решений, в которой прямая  возрастают в направлении вектора
возрастают в направлении вектора  , поэтому прямую
, поэтому прямую  . Прямая дважды становится опорной по отношению к многоугольнику решений (в точках
. Прямая дважды становится опорной по отношению к многоугольнику решений (в точках  и
и  ), причем минимальное значение принимает в точке
), причем минимальное значение принимает в точке  находим, решая систему уравнений прямых
находим, решая систему уравнений прямых  и
и  .
. называют решением или планом задачи.
называют решением или планом задачи. из свободных членов называется вектором правых частей.
из свободных членов называется вектором правых частей.


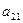



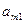



 , где
, где  ,
, 
 , то полученный план является оптимальным.
, то полученный план является оптимальным.


