
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закон всемирного тяготения и задача двух телСодержание книги
Поиск на нашем сайте
В частном случае задачи двух тел рассматривается движение тела меньшей массы т относительно тела большей массы М, принимаемого за неподвижное и называемого центральным телом. Линейная скорость v движущегося тела относительно центрального определяется интегралом энергии
где μ=G(Μ+m), а — большая полуось орбиты тела меньшей массы, r — радиус-вектор того же тела, G — гравитационная постоянная. Если масса т движущегося тела пренебрежимо мала в сравнении с массой Μ центрального тела, то задача двух тел называется ограниченной и тогда μ = GΜ. Согласно интегралу энергии, чтобы тело меньшей массы обращалось вокруг центрального тела по круговой орбите (эксцентриситет е=0) радиусом r=а, оно должно на этом расстоянии иметь скорость
называемую круговой скоростью. Как средняя скорость движения тела она может быть также подсчитана по периоду обращения Τ и большой полуоси а орбиты тела:
Если движущееся тело на расстоянии r от центрального тела имеет скорость
то орбитой будет парабола (е=1, а=∞). Поэтому скорость vп называется параболической. Если v>vп, то движущееся тело пройдет мимо центрального тела по гиперболе (e>1). В каждой точке орбиты с радиус-вектором r скорость тела
Точка эллиптической орбиты, ближайшая к центральному телу, называется перицентром, а наиболее удаленная от него—апоцентром. Эти точки получают конкретные наименования но названию центрального тела, и некоторые из них приведены в нижеследующей таблице:
В перицентре, при r = q = а(1—е), тело-спутник обладает наибольшей скоростью
а в апоцентре, при r = Q = a (1 + e), — наименьшей скоростью
Скорость небесных тел всегда выражается в км/с, а расстояния могут быть заданы в астрономических единицах, километрах или радиусах центрального тела. Поэтому в формулы (64), (65) и (66) необходимо подставлять значения расстояний в одинаковых единицах измерения. В поле тяготения Солнца, на произвольном от него расстоянии r, выраженном в астрономических единицах (а. е.), круговая скорость
Если расстояния r заданы в километрах, а масса центрального тела выражена в массах Земли, то круговая скорость
Наконец, при измерении масс в массах Земли и расстояний в радиусах Земли круговая скорость
Средняя или круговая скорость va тела, обращающегося вокруг центрального тела по эллиптической орбите с большой полуосью а, также вычисляется по формулам (67), (68) и (69) подстановкой в них r=а. Подстановка в формулы (68) и (69) r = R (радиус небесного тела) дает значение круговой скорости wк у поверхности этого тела, называемой в космонавтике первой космической скоростью. Вторая космическая скорость Wп—Wк√2. Очевидно, что
где r отсчитывается от центра небесного тела и выражается в его радиусах. Третий обобщенный закон Кеплера
применим к любым системам тел с массами m1 и m2, обращающихся с периодами Т1 и Т2 вокруг своих центральных тел (с массами M1 и М2) по эллиптическим орбитам, большие полуоси которых соответственно равны а1 и а2. Массы планет и их спутников выражаются обычно в массах Земли (реже — в массах Солнца, в тоннах и килограммах), большие полуоси орбит — в астрономических единицах или в километрах, а периоды обращения— в годах и сутках, а иногда — в часах и минутах. При вычислениях по формуле (71) выбор системы единиц не имеет значения, лишь бы однородные величины были выражены в одинаковых единицах. Если же этот закон используется в виде
то решение задач проводится обязательно в определенной системе единиц, так как в разных системах численное значение гравитационной постоянной различно. Если периоды обращения заданы в земных средних сутках, расстояния — в километрах и массы тел — в массах Земли, то третий закон Кеплера имеет вид Т2 (М+m) = 132,7 · 10-16а3. (73) Пример 1. Комета Галлея прошла в 1910 г. свой перигелий на гелиоцентрическом расстоянии 0,587 а. е. со скоростью 54,52 км/с, а комета Икейи — Секи в 1965 г. — на перигельном расстоянии 0,0083 а.е. со скоростью 480 км/с. По каким орбитам двигались эти кометы и когда они возвратятся к Солнцу? Данные: комета Галлея, q = 0,587 а.е., vq = = 54,52 км/с; комета Икейи —Секи, q = 0,0083 а. е., vq = 480 км/с. Решение. Чтобы определить род орбиты, необходимо подсчитать круговую νк и параболическую vп скорость кометы относительно Солнца на заданных расстояниях q от него и сопоставить вычисленные скорости с действительными. Комета Галлея. Согласно формуле (67), на расстоянии q = 0,587 а.е. круговая скорость
а по формуле (63) параболическая скорость
Поскольку vк<vq<vп и в то же время uq близка к vп, то комета Галлея обращается вокруг Солнца по очень вытянутой эллиптической орбите, большая полуось которой вычисляется по формулам (64) и (67). Положив в формуле (64) r=q, найдем
По формуле (67) круговая скорость кометы равна
Подставив эту формулу в предыдущее выражение, получим:
Откуда
По формуле (35) эксцентриситет орбиты
По третьему закону Кеплера (39) период обращения кометы T = a√a=18√18≈76 лет. Следовательно, комета Галлея снова вернется к Солнцу и будет видна в 1986 г. Комета Икейи-Секи. На расстоянии r = q = 0,0083 а. е. круговая скорость
и параболическая скорость vп=vк√2=327·1.41 = 461 км/с <!--[endif]--> т. е. скорость кометы в перигелии vq>vп; комета прошла вблизи Солнца но гиперболической орбите и больше к нему не вернется. Пример 2. Для астероида Икара найти среднюю скорость, скорость в перигелии, в афелии и в точке орбиты с истинной аномалией 90°, а также круговую и параболическую скорость на тех же расстояниях от Солнца. Большая полуось и эксцентриситет орбиты Икара равны 1,078 а. е. и 0,826. Данные: Икар, а = 1,078 а.е., е = 0,826, θ=90°. Решение. По формулам (34), (35) и (36) находим гелиоцентрические расстояния: при θ=90°
q=1,078 (1—0,826) =0,188 а. е., Q= 1,078 (1+0,826) = 1,968 а. е. по (67), (65) и (66), круговая скорость планеты va=29,8 /√1,078=28,7 км/с скорость в перигелии vq=28,7 √(1,968/0,188) = 93,0 км/с и скорость в афелии
По формуле (64) скорость при θ=90°
На расстоянии q = 0,188 а.е., согласно формулам (67) и (63), круговая скорость vкq=29,8/√0,188 = 68,7 км/с и параболическая скорость vпq = 68,7 · 1,41 =96,9 км/с, Т. е. vкq<vq<vпq На расстоянии Q= 1,968 а. е. vкQ=29,8/√1,968=21,2 и vпQ = 21,2·1,41·29,9 км/с, т. е. VQ<VкQ<vпQ. На расстоянии r=0,342 а. е. vкr=29,8/√0,342=50,8 км/с и vпr = 50,8· 1,41 = 71,6 км/с, Т. е. vкr<vr<vпr Пример 3. Найти массу Юпитера по движению его спутника Ио, обращающегося вокруг планеты с периодом в 1д,769 по круговой орбите на расстоянии в 421,6 · 103 км. Данные: спутник, T=1д,769, α=421,6·103 км. Решeние. Формула (73) дает
Пример 4. Вычислить первую и вторую космическую скорость на Юпитере, круговую и параболическую скорость па расстояниях в 3 и 8 его радиусов от поверхности, а также скорость его первого спутника Ио, обращающегося по круговой орбите радиусом 421,6·103 км. Масса Юпитера равна 318 масс Земли, а средний радиус—10,9 радиуса Земли. Данные: Юпитер, М=318, R=10,9; расстояния: 3R и 8R от поверхности, или от центра планеты r1 = 4R и r2=9R; спутник Ио, T=1д,769, α=421,6·103 км. Решение. По формуле (69), первая космическая скорость
и вторая космическая скорость, по (63), wп = wк √2 = 42,7 · 1,41 = 60,2 км/с. По формулам (70), круговая скорость на различных расстояниях vк1 = wк/√r1=42,7/√4 = 21,4 км/с И vк2 = wк/√r2 = 42,7/√9 = 14,2 км/с, а параболическая скорость vп1 = wп/√r1 = 60,2/√4 = 30,1 км/с и vп2 = wп/√r2=60,2/√9 = 20,1 км/с. Согласно формуле (68), скорость спутника Ио
Задача 170. Чему равна круговая и параболическая скорость относительно Солнца на средних расстояниях Венеры (0,723 а. е.), Земли (1,00 а. е.), Юпитера (5,20 а. е.) и Плутона (39,5 а. е.)? По общим результатам найти и объяснить найденную закономерность. Расстояния планет от Солнца указаны в скобках. Задача 171. Вычислить скорость малых планет Ахиллеса и Гектора в перигелии и афелии, если их круговая скорость близка к 13,1 км/с, а эксцентриситеты орбит соответственно равны 0,148 и 0,024. Примерно на каком среднем гелиоцентрическом расстоянии находятся эти планеты? Задача 172. Большая полуось и эксцентриситет op-биты Меркурия равны 0,387 а. е. и 0,206, а орбиты Марса — 1,524 а. е. и 0,093. Найти среднюю скорость этих планет, их скорость в перигелии и в афелии. Задача 173. Считая орбиты планет круговыми и лежащими в плоскости эклиптики, найти лучевую скорость Меркурия, Венеры и Марса во время их основных конфигураций. Необходимые для решения данные заимствовать из задач 170 и 172. (Лучевой скоростью называется проекция пространственной скорости на луч зрения наблюдателя, т. е. в данном случае на направление от Земли к планете.) Задача 174. Вычислить скорость астероидов Лидии и Адониса на их среднем, перигелыюм и афелийном расстояниях, а также круговую и параболическую скорость на этих расстояниях. Большая полуось и эксцентриситет орбиты первого астероида равны 2,73 а. е. и 0,078, а второго— 1,97 а. е. и 0,778. Задача 175. На каких гелиоцентрических расстояниях скорость Меркурия равна 56,1 км/с и 41,7 км/с? Большая полуось орбиты планеты 0,387 а. е. Задача 176. С какой скоростью относительно Солнца проходил Марс в эпоху великого противостояния при геоцентрическом расстоянии в 57,15·106 км? Сопоставить эту скорость с круговой и параболической скоростью на том же расстоянии от Солнца. Большая полуось орбиты Марса равна 1,524 а. е. Задача 177. Решить предыдущую задачу для астероида Эрота, если он в эпоху великого противостояния проходил свой перигелий 23 января 1975 г. на расстоянии 22,59·106 км от Земли. Период обращения Эрота вокруг Солнца равен 1,760 года. Задача 178. На каком расстоянии от Солнца прошла комета, если ее скорость на этом расстоянии равнялась 65 км/с и комета двигалась по параболической орбите? Задача 179. Комета 1931 IV прошла свой перигелий на расстоянии 0,07 а. е. от Солнца со скоростью 160 км/с, а комета 1945 II —на расстоянии 1,24 а. е. со скоростью 36,5 км/с. Определить род орбит, по которым двигались эти кометы и установить, вернутся ли они к Солнцу и когда именно. Задача 180. Синодический период обращения астероида Колхиды равен 1,298 года, а его скорость в перигелии — 20,48 км/с. Чему равны сидерический период обращения астероида, большая полуось и эксцентриситет его орбиты, перйгельное и афелийное расстояния, а также скорость на среднем гелиоцентрическом расстоянии и в афелии? Задача 181. Эксцентриситет орбиты астероида Узбекистании равен 0,092, а его скорость в афелии— 15,21 км/с. Найти большую полуось орбиты астероида, его звездный и синодический периоды обращения, скорость в перигелии и при истинной аномалии в 30, 90 и 120°. Задача 182. Определить массу Марса в массах Земли по движению его спутника Деймоса, находящегося от планеты на среднем расстоянии в 23,5·103 км и обращающегося вокруг Марса за 1,26 сут. Период обращения Луны вокруг Земли равен 27,32 сут и большая полуось лунной орбиты —384,4·103 км. Задача 183. Узнать массу Урана по движению его четвертого спутника Оберона, обращающегося вокруг планеты за 13,46 сут на среднем расстоянии в 587 тыс. км. Задача 184. По параметрам обращения Земли вычислить массу Солнца в земных массах. Задача 185. Определить сидерические периоды и среднюю скорость спутников Сатурна, Мимада и Фебы, обращающихся вокруг планеты на средних расстояниях, соответственно 185,4·103 км и 12960·103 км. Масса Сатурна в 95,2 раза превышает массу Земли. Задача 186. По данным предыдущей задачи вычислить скорость тех же спутников Сатурна в перикронии и апокро-нии, а также круговую и параболическую скорость на указанных расстояниях от Сатурна. Эксцентриситеты орбит спутников в той же последовательности равны 0,020 и 0,166. Задача 187. Найти большую полуось орбит и среднюю скорость спутников Юпитера Ио и Каллисто, обращающихся вокруг планеты с периодами соответственно в 1д,769 и 16д,689. Масса Юпитера в 318 раз больше массы Земли. Задача 188. Как должна измениться масса центрального тела, чтобы у его спутника среднее расстояние увеличилось в k раз, а период обращения в n раз и, в частности, при k=n? Задача 189. Какой должна быть масса Солнца, чтобы Земля обращалась вокруг него с современным периодом, но на вдвое большем расстоянии? Как изменятся при этом периоды обращения Марса и Сатурна, если их расстояния останутся неизменными? Современные периоды обращения этих планет— 1,881 года и 29,46 года. Задача 190. Определить гипотетический период обращения Луны вокруг Земли при условии, что масса Земли возросла бы в четыре раза, а Луна оказалась на вдвое большем расстоянии. Современный период обращения Луны равен 27д,32. Задача 191. Вычислить круговую и параболическую скорость на поверхности Земли и на расстояниях в 1, 8 и 59,3 ее радиуса от поверхности. Задача 192. Среднее геоцентрическое расстояние Лупы — 384 400 км, а средний эксцентриситет ее орбиты — 0,0549. Найти среднюю, перигейиую и апогейную скорости Луны и сопоставить их с результатами предыдущей задачи. Задача 193. Чему равна круговая и параболическая скорость на поверхности Солнца и на расстоянии трех и восьми радиусов от его поверхности? Масса Солнца в 333 000 раз превышает массу Земли, а его радиус равен 109,1 земного. Задача 194. Определить круговую и параболическую скорость на поверхности Луны, Венеры и Марса. Массы и радиусы этих тел в земных параметрах: Луны 0,0123 и 0,272, Венеры 0,815 и 0,950 и Марса 0,107 и 0,533. Ответы - Закон всемирного тяготения и задача двух тел
Искусственные небесные тела При запуске искусственных небесных тел им сообщается начальная скорость (скорость запуска) vн зависящая от рассчитанной орбиты. Начальная скорость сообщается космическим двигателем на некоторой высоте hн над поверхностью центрального тела (вокруг которого запускается спутник), г. е. от его центра на расстоянии r=R+hн, (74) где R — средний радиус этого тела. В частности, при запуске вокруг Земли R = 6371 км ~ 6370 км, что следует иметь в виду при решении задач этого раздела. Форма и размеры эллиптической орбиты искусственного спутника определяются целями запуска (рис. 8).
Рис. 8. Эллиптическая орбита искусственного спутника Центр центрального тела является одним из фокусов орбиты, а ее большая полуось
причем перицентрическое расстояние q = R+hq (76) и апоцентрическое расстояние Q = R+hQ, (77) где hq — наименьшая высота (высота перицентра) и hQ — наибольшая высота (высота апоцентра) искусственного спутника над поверхностью тела. Для искусственных спутников и орбитальных кораблей Земли hq — высота перигея, hQ — высота апогея, q — перигейное расстояние и Q — апогейное расстояние. Эксцентриситет орбиты определяется формулой (35). Скорость искусственных небесных тел обычно выражается в км/с и вычисляется по формулам (40), (64) — (66) и (68) — (70). Периоды обращения искусственных спутников принято измерять в минутах, а их расстояния—в километрах, и поэтому третий закон Кеплера имеет вид
или
и
где M — масса центрального тела, выраженная в массах Земли. По параметрам обращения искусственного спутника можно вычислить массу центрального тела. Продолжительность полета искусственных спутников над полушарием центрального тела, расположенным под перицентром орбиты (перицентрийное полушарие),
где Τ — период обращения спутника и е — эксцентриситет его орбиты. Над противоположным (апоцентрийным) полушарием спутник пролетает за интервал времени τ=T—t. (82) Формулы (75) — (82) вполне применимы и к движению естественных спутников планет. В полете с одной планеты к другой межпланетная станция (межпланетный корабль) становится спутником Солнца и движется в его поле тяготения по законам движения планет. Простейшей траекторией полета является полуэллиптическая, вершины (апсиды) которой касаются орбит планеты запуска (с нее производится запуск) и планеты сближения (к ней направляется станция). Пренебрегая в первом приближении наклонением и эллиптичностью планетных орбит, можно проводить расчеты по значениям их больших полуосей a1 (планеты запуска) и a2 (планеты сближения), заданных в астрономических единицах (а. е.). При полете к верхней планете (рис. 9) запуск станции осуществляется на ее перигельном расстоянии q=a1 (83) в прямом направлении; афелийное же расстояние станции Q=a2. (84)
Рис. 9. Простейшая орбита межпланетного корабля При направлении станции к нижней планете q = a2 и Большая полуось а гелиоцентрической орбиты межпланетной станции вычисляется по формуле (37), эксцентриситет орбиты — по формуле (35), а продолжительность полета, выраженная в годах,
где а — в астрономических единицах. При необходимости Δt переводится в сутки. Гелиоцентрическая скорость полета станции дается формулами (41), (64), (65) и (66). При запуске к верхней планете начальная гелиоцентрическая скорость Vн = Vq а при запуске к нижней планете Vн = VQ причем в эту скорость Vн входит орбитальная (в рассматриваемом здесь простейшем случае—круговая) скорость V1 планеты запуска. Следовательно, чтобы межпланетная станция вышла на расчетную гелиоцентрическую орбиту, необходимо сообщить ей дополнительную скорость Vд = Vн - V1 (86) Но, чтобы покинуть планету запуска, станция должна еще преодолеть ее притяжение, на что требуется кинетическая энергия где т — масса станции и wп — вторая космическая (критическая) скорость на поверхности этой планеты. Поэтому скорость запуска vн станции с планеты, называемая также начальной планетоцентрической скоростью, найдется из равенства
откуда
День запуска t1 межпланетной станции не может быть произвольным и выбирается по подходящей конфигурации Δλ2 планеты сближения Ρ (см. рис. 9), иначе станция придет в намеченный район встречи либо раньше, либо позже планеты. У планеты сближения с сидерическим периодом обращения Т2 среднее суточное движение.
и за найденную по формуле (85) продолжительность полета станции Δt (выраженную в сутках) планета должна прийти в район встречи A, пройдя по своей орбите путь
Следовательно, в день t1 старта межпланетной станции разность гелиоцентрической долготы планеты сближения (l2) и планеты запуска (l1) должна быть l2- l1 = 180°—L2 = 180° — ω2Δt (88) и по этой разности нетрудно найти в астрономическом календаре-ежегоднике на текущий год подходящий день l1. В этот день расстояние между планетами
а конфигурация Δλ2 планеты сближения вычисляется либо из равенства
либо по формуле
Легко видеть, что при L2 < 180° найденная элонгация будет западной, а при L2 > 180° — восточной. Очевидно, межпланетная станция подойдет к планете сближения в день t2 = t1 + Δt. Пример 1. Запущенный 19 апреля 1973 г. в Советском Союзе искусственный спутник «Интеркосмос— Коперник-500» предназначен для исследования рентгеновского излучения Солнца и верхних слоев земной атмосферы в пределах от 200 до 1550 км над земной поверхностью. Определить параметры движения спутника. Данные: спутник, hq=200 км, hQ=1550 км; Земля, R = 6370 км, M = 1. Решение. По формуле (75) большая полуось орбиты спутника
а по (76) и (77) его перигейное расстояние q =R+hq = 6370 + 200=6570 км и апогейное расстояние Q = R+hQ = 6370 + 1550 = 7920 км. Эксцентриситет орбиты, согласно (35),
а по формуле (79) период обращения
так как масса Земли M=1. Формула (68) дает круговую скорость спутника
а формулы (65) и (66) —его скорость в перигее
и в апогее Согласно формулам (81) и (82), спутник пролетает над перигейным полушарием Земли за промежуток времени
а в течение т = Т — t = 102 — 45 = 57м движется над апогейным полушарием. Пример 2. Какую ареоцентрическую скорость и на каком максимальном расстоянии от поверхности Марса нужно сообщить космическому аппарату, чтобы он стал искусственным спутником планеты и обращался вокруг нее с периодом в 2ч40м по эллиптической орбите с эксцентриситетом 0,250? Масса Марса равна 0,107, а его радиус — 3400 км. Данные: Марс, M = 0,107, R = 3400 км; аппарат, T = 2ч40м = 160м, е=0,250. Решение. Согласно формуле (80), у орбиты искусственного спутника большая полуось
и расстояние апоария Q = a(l+e) =4650· 1,250=5810 км, откуда, по (77), максимальное расстояние от поверхности планеты hQ = Q—R = 5810—3400 = 2410 км. По (68), круговая скорость спутника
и тогда, согласно (66), искомая скорость в апоарии
Пример 3. Выяснить обстоятельства полета межпланетного корабля с Венеры к Юпитеру. Среднее гелиоцентрическое расстояние Юпитера — 5,203 а. е., а Венеры — 0,723 а. е. Критическая (вторая космическая) скорость на поверхности Венеры 10,36 км/с; среднее суточное движение Юпитера 0°,0831. Данные: планета запуска, Венера, а1 = 0,723, а.е., wп = 10,36 км/с; планета сближения,, Юпитер, а2 = 5,203 а. е., ω2 = 0°,831 ~ 5' (в сутки). Решение. Изображаем орбиты обеих планет и гелиоцентрическую орбиту межпланетного корабля (см. рис. 9). Поскольку корабль стартует с нижней планеты к верхней, то запуск происходит в перигелии, и, согласно формулам (83), (84), (75), (35) и (85), перигельное расстояние корабля q = a1 = 0,723 а. е., афелийное расстояние Q = a2 = 5,203 а. е., большая, полуось орбиты
эксцентриситет орбиты
и продолжительность полета к Юпитеру
По формуле (41) гелиоцентрическая круговая скорость корабля
а по (65) —скорость в перигелии, она же начальная гелиоцентрическая скорость корабля,
Так как орбитальная скорость Венеры
то, согласно (86), дополнительная скорость vд = Vн—V1 = 46,4—35,0 = 11,4 км/с, откуда, по (87), скорость запуска корабля с Венеры
За промежуток времени Δt = 2,55 года = 2,55·365 сут Юпитер пройдет по своей орбите путь L2 = ω2Δt = 0°,0831·2,55·365 = 77°,4, и поэтому, по (88), в день старта корабля разность гелиоцентрической долготы Юпитера и Венеры l2—l1 = 180°—L2= 180°—77°,4 = 102°,6, а конфигурация Δλ2 Юпитера, видимая с Венеры, находится по формуле (91):
откуда Δλ2 = 69°,9. Поскольку L2 = 77°,4 < 180°, то найденная конфигурация представляет собой западную элонгацию. Этот же результат получается и по формулам (89) и (90). Задача 195. Определить скорость запуска и периоды обращения искусственных спутников Земли, движущихся вокруг нее по круговым орбитам на расстояниях половины и двух ее радиусов от поверхности. Задача 196. Решить предыдущую задачу для искусственных спутников Марса и Юпитера. Массы и радиусы в сравнении с земными: Марса — 0,107 и 0,533, а Юпитера — 318 и 10,9. Задача 197. Как изменятся периоды и скорость обращения спутников предыдущих задач, если масса центрального тела возрастет в n раз, а его радиус — в m раз и в частном случае при m = n? Задача 198. На какой высоте над земной поверхностью и с какой скоростью движутся по круговым орбитам искусственные спутники с периодами обращения в 90м, 150м, и 3ч? Радиус Земли принять равным 6370 км. Задача 199. Вычислить высоту над земной поверхностью и скорость стационарного искусственного спутника, т. е. спутника, неподвижно висящего над одной и той же точкой земного экватора. Задача 200. Решить предыдущую задачу для стационарных искусственных спутников планет, указанных в задаче 196. Период вращения Марса — 24ч37м,4, а Юпитера — 9ч50м,5. Задача 201. Найти скорость и периоды обращения искусственных спутников при одинаковой высоте в 200 и 1000 км над поверхностью Земли, Луны, Марса и Юпитера. Массы этих небесных тел в той же последовательности равны 1, 0,0123, 0,107 и 318, а радиусы — 6370, 1738, 3400 и 71400 км. Задача 202. На сколько градусов и в каком направлении должна смещаться трасса полета полярных искусственных спутников * за один оборот при их движении по круговым орбитам со скоростью 7 км/с и 2 км/с вокруг Земли, Меркурия и Венеры? Период вращения Меркурия — 58д,65, а Венеры — 243д,2 (вращение планеты обратное). Необходимые сведения см. в задаче 204. * Трассой полета называется проекция орбиты спутника на поверхность небесного тела. Полярный спутник проходит над обоими полюсами планеты. Задача 203. По каким орбитам будут двигаться искусственные небесные тела, запущенные с горизонтальной скоростью 9,5 км/с на высоте 200 км над поверхностью Земли, Марса и Юпитера? Необходимые сведения заимствовать из задачи 201. Задача 204. На какой минимальной высоте и с какой скоростью должны быть выведены на эллиптические орбиты с эксцентриситетом 0,100 и 0,600 искусственные спутники, чтобы они обращались с периодами в 2ч и 8ч вокруг Меркурия и Венеры, массы которых, в сравнении с земной, соответственно 0,055 и 0,815, а радиусы — 2440 км и 6050 км? Задача 205. Какую долю своего периода обращения пролетают над перицентрийным и апоцентрийным полушариями планет искусственные спутники при эксцентриситетах их орбит 0,100 и 0,400? Задача 206. Сколько времени пролетали над перигейным и апогейным полушариями орбитальная станция «Салют-5» (выведена на орбиту 22 июня 1976 г.) и спутник связи «Молния-2» (выведен на орбиту 25 декабря 1973 г.), если «Салют-5» обращался в пределах высоты от 258 км до 283 км, а «Молния-2» —по орбите с большой полуосью 27 030 км и высотой апогея 40 860 км? Задача 207. Найти массу Луны (в массах Земли) по движению ее искусственных спутников, обращавшихся над лунной поверхностью в пределах высоты: «Луна-19» (28 ноября 1971 г.) от 77 км до 385 км, с периодом в 2ч11м; «Луна-20» (19 февраля 1972 г.) от 21 км до 100 км, с периодом в 1ч54м. В скобках указана дата выведения спутника на селеноцентрическую орбиту. Диаметр Луны — 3476 км. Задача 208. По данным и результату предыдущей задачи рассчитать круговую и предельные селеноцентрические скорости спутников Луны. Задача 209. Определить массу Марса по движению его естественного спутника Деймоса и советского искусственного спутника «Марс-5» (12 февраля 1974 г.). Деймос обращается вокруг планеты с периодом 1д,262 на среднем расстоянии 23 500 км, а «Марс-5» — с периодом 25ч,0, в пределах высоты над поверхностью планеты от 1760 км до 32 500 км. Радиус Марса — 3400 км. Задача 210. Советская автоматическая межпланетная станция «Венера-10», ставшая 25 октября 1975 г. вторым искусственным спутником Венеры, обращалась в те дни вокруг планеты с периодом 49ч23м в пределах от 1400 км до 114 000 км над ее поверхностью. Определить массу Венеры, приняв ее радиус равным 6050 км. Задача 211. Первый в истории человечества облет Земли был осуществлен Героем Советского Союза Ю. А, Гагариным на космическом корабле «Восток» 12 апреля 1961 г. в пределах высоты от 181 км до 327 км над земной поверхностью. Определить большую полуось и эксцентриситет орбиты корабля, период его обращения вокруг Земли, его среднюю и предельные скорости, а также продолжительность полета над перигейным и апогейным полушариями Земли. Задача 212. Решить предыдущую задачу для спутника связи «Молния-2», выведенного 5 апреля 1973 г. на орбиту вокруг Земли в пределах высоты от 500 до 39 100 км. Задача 213. Как изменились бы параметры полета спутника связи предыдущей задачи, если бы он в пределах той же высоты обращался вокруг Меркурия и Юпитера? Необходимые данные заимствовать из задач 201 и 204. Задача 214. Спутник связи «Молния-3», выведенный 14 апреля 1975 г. на орбиту с высотой перигея 636 км над южным полушарием Земли, обращается вокруг планеты с периодом 12ч16м. Найти большую полуось и эксцентриситет орбиты спутника, его апогейную высоту, скорость в перигее и апогее и продолжительность полета над противоположными полушариями Земли. Задача 215. Вычислить все основные параметры полета искусственного спутника Луны «Луна-22», выведенного на орбиту 9 июня 1974 г., если он обращался с периодом в 2ч02м и поднимался в апоселении на высоту в 244 км над лунной поверхностью. Сведения о Луне заимствовать из задачи 201. Задача 216. Определить большую полуось и эксцентриситет простейшей эллиптической орбиты космического корабля, продолжительность его полета от Земли до Марса и скорость запуска с Земли, если среднее гелиоцентрическое расстояние Марса равно 1,524 а. е. Среднюю орбитальную скорость Земли принять 29,8 км/с. Задача 217. По данным и результатам предыдущей задачи найти конфигурацию Марса, наиболее благоприятную для запуска к нему с Земли космического корабля. Период обращения Марса вокруг Солнца равен 687 сут. Задача 218. Вычислить скорость запуска космического корабля с Марса для полета к Земле по простейшей орбите и благоприятствующую этому конфигурацию Земли. Среднее гелиоцентрическое расстояние Марса — 1,524 а. е., его масса —0,107 и радиус — 0,533 в сравнении с земными. Задача 219. По данным и результатам задач 216, 217 и 218 найти наименьшую продолжительность путеществия с Земли на Марс и обратно (подходящие даты для старта кораблей установить по астрономическим календарям-ежегодникам). Задача 220. Определить параметры, указанные в задачах 216, 217 и 218 для полета космического корабля с Земли к Венере и обратно к Земле. Среднее гелиоцентрическое расстояние Венеры равно 0,723 а. е., ее масса — 0,815 и радиус — 0,950 в сравнении с земными. Задача 221. Через какие промежутки времени целесообразно запускать с Земли к планетам космические станции? Ответы - Искусственные небесные тела
Тяжесть и тяготение Согласно закону всемирного тяготения, на поверхности сфероидального небесного тела с массой M и радиусом R гравитационное ускорение*
а на поверхности Земли то же ускорение
откуда, поделив первое равенство (92) на второе, получим:
где обязательно Μ выражается в массах Земли и R — в радиусах Земли, а В поле тяготения небесного тела на произвольном расстоянии от него гравитационное ускорение
или, учитывая равенство (92),
В этой формуле r и R могут быть выражены в любых, но обязательно одинаковых единицах длины. * Ослабление g вращением тела здесь не рассматривается. Пример 1. Найти гравитационное ускорение, сообщаемое Юпитером своему второму спутнику Европе, находящемуся от планеты на среднем
|
||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 2414; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.232.108 (0.017 с.) |

 (61)
(61) (62)
(62) (40)
(40)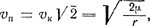 (63)
(63) (64)
(64) (65)
(65) (66)
(66)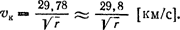 (67)
(67) (68)
(68) (69)
(69) (70)
(70) (71)
(71) (72)
(72)

















 (78)
(78) (79)
(79) (80)
(80) (81)
(81)
 (85)
(85) ,
,
 (87)
(87)

 (89)
(89) (90)
(90) (91)
(91)














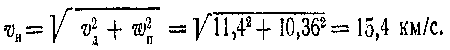



 (92)
(92)
 (93)
(93) — относительное гравитационное ускорение в сравнении с земным.
— относительное гравитационное ускорение в сравнении с земным.
 (94)
(94)


