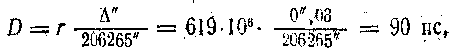Движение звезд и галактик в пространстве

Пространственная скорость V звезд всегда определяется относительно Солнца (рис. 10) и вычисляется по лучевой скорости V_r направленной вдоль луча r, соединяющего звезду с Солнцем, и по тангенциальной скорости V_t.

(141)

 

Рис. 10, Движение звезды относительно Солнца

Направление пространственной скорости V звезды характеризуется углом θ между нею и лучом зрения наблюдателя; очевидно,

cos θ = V_r / V

и sin θ =V_t/V (142)

причем 0° ≤ θ ≤ 180°.

Из наблюдений определяется лучевая скорость v_r звезды относительно Земли. Если в спектре звезды линия с длиной волны λ сдвинута от своего нормального (лабораторного) положения на величину Δх мм, а дисперсия спектрограммы на данном ее участке равна D Å/мм, то смещение линии, выраженное в Å,

Δλ = λ' - λ = Δх · D (143)

и, по (138), лучевая скорость

v_r = c (Δλ / λ)

где с = 3·10⁵ км/с — скорость света.

Тогда лучевая скорость в километрах в секунду относительно Солнца

V_r = v_r — 29,8·sin (λ_* — λ ) cos β_*, (144)

где λ_* — эклиптическая долгота и β_*— эклиптическая широта звезды, λ — эклиптическая долгота Солнца в день получения спектрограммы звезды (заимствуется из астрономического ежегодника), а число 29,8 выражает круговую скорость Земли в километрах в секунду.

Скорость V_r (или v_r) положительна при направлении от Солнца (или от Земли) и отрицательна при обратном направлении.

Тангенциальная скорость V_t звезды в километрах в секунду определяется по ее годичному параллаксу π и собственному движению μ, т. е. по дуге, на которую смещается звезда на небе за 1 год:

(145)

причем μ и π выражены в секундах дуги ("), а расстояние r до звезды — в парсеках.

В свою очередь, μ определяется по изменению экваториальных координат α и δ звезды за год (с учетюм прецессии):

(146)

причем компонент собственного движения звезды по прямому восхождению μ_a выражен в секундах времени (с), а компонент по склонению μ_δ —в секундах дуги (").

Направление собственного движения μ определяется позиционным углом ψ, отсчитываемым от направления к северному полюсу мира:

(147)

причём ψ в пределах от 0° до 360°.

По рисунку 10 нетрудно подсчитать интервал времени Δt, отделяющий нас от эпохи, в которую звезда проходила (или пройдет) на минимальном расстоянии rm от Солнца.

У галактик и квазаров собственное движение μ = 0, и поэтому у них определяется только лучевая скорость V_r, а так как эта скорость велика, то скоростью Земли пренебрегают и тогда V_r = v_r. Обозначая Δλ/λ = z, получим для сравнительно близких галактик, у которых z ≤ 0,1,

V_r = cz, (148)

и, согласно закону Хабба, их расстояние в мегапарсеках (Мпс) *

r = V_r / H = V_r / 50 (149)

где современное значение постоянной Хаббла H = 50 км/с·Мпс.

Для далеких галактик и квазаров, у которых z > 0,1, следует пользоваться релятивистской формулой

(150)

а оценка их расстояний зависит от принятой космологической модели Вселенной. Так, в закрытой пульсирующей

модели

(151),

а в открытой модели Эйнштейна — де Ситтера

(152)

Пример 1. В спектре звезды линия гелия с длиной волны 5016 Å сдвинута на 0,017 мм к красному концу, при дисперсии спектрограммы на этом участке в 20 Å/мм. Эклиптическая долгота звезды равна 47°55' и ее эклиптическая широта — 26°45', а во время фотографирования спектра эклиптическая долгота Солнца была близкой к 223° 14'. Определить лучевую скорость звезды.

Данные: спектр, λ = 5016 Å, Δx = +0,017 мм,.

D=20 Å/мм; звезда, λ* = 47°55', β* = —26°45'; Солнце, λ = 223° 14'.

Решение. По формулам (143) и (138) находим смещение спектральной линии:

Δλ = ΔxD = +0,017·20 = +0,34Å

и лучевую скорость звезды относительно Земли:

Чтобы использовать формулу (144) для вычисления лучевой скорости Vr звезды относительно Солнца, необходимо по таблицам найти

sin (λ*—λ ) = sin (47°55'—223° 14') = —0,0816
и cosβ* = cos (—26°45') = + 0,8930,

и тогда

V_r—v_r—29,8·sin(λ_*—λ )cosβ_* = +20,5+29,8·0,0816·0,8930 = +22,7; V_r = +22,7 км/с.

Пример 2. В спектре квазара, фотографический блеск которого 15m,5 и угловой диаметр 0",03, эмиссионная линия водорода Η_β с длиной волны 4861 Å занимает положение, соответствующее длине волны 5421 Å. Найти лучевую скорость, расстояние, линейные размеры и светимость этого квазара.

Данные: m_pg = 15m,5, Δ = 0",03;

Η_β , λ' = 5421 Å, λ = 4861 Å.

Решение. По формуле (143), смещение спектральной линии водорода

Δλ = λ" — λ = 5421 - 4861 = + 560Å

и

и так как z > 0,1 то, согласно (150), лучевая скорость

или V_r = 0,108·3·10⁵ км/с = +32400 км/с.

По формуле (151), в закрытой пульсирующей модели Вселенной расстояние до квазара

r = 619 Μпс =619· 10⁶ пс.

или r = 619·10⁶·3,26 cв, лет = 2,02· 10⁹ cв, лет

Тогда, по (55), линейный диаметр квазара

или D = 90 · 3,26 = 293 св. года.

Согласно (117), его абсолютная фотографическая звездная величина

M_pg = m_pg + 5 — 5 lgr = 15^m, 5 + 5 — lg619·10⁶ = — 23^m,5

и, по формуле (120), логарифм светимости

lgL_pg = 0,4(M _pg - M_pg) = 0,4·(5^m,36 + 23^m,5) = 11,54,

откуда светимость L_pg = 347·10⁹, т. е. равна светимости 347 миллиардов звезд типа Солнца.

Те же величины в модели Эйнштейна — де Ситтера получаются по формуле (152):

r = 636 Мпс;

или r = 636·10⁶·3,26 св. лет. = 2,07·10⁹ св. лет, D = 92,5 пс = 302 св. года и с той же степенью точности M_pg = — 23^m,5 и L_pg = 347·10⁹

Задача 345. Линии поглощения водорода Η_β, и Н_δ, длина волны которых 4861 Å и 4102 Å, смещены в спектре звезды к красному концу соответственно на 0,66 и 0,56 Å. Определить лучевую скорость звезды относительно Земли в ночь наблюдений.

Задача 346. Решить предыдущую задачу для звезды Регула (а Льва), если те же линии в ее спектре смещены к фиолетовому концу соответственно на 0,32 Å и 0,27 Å.

Задача 347. В какую сторону спектра и на сколько миллиметров сдвинуты линии поглощения железа с длиной волны 5270 Å и 4308 Å в спектрограмме, звезды с лучевой скоростью — 60 км/с, если дисперсия спектрограммы на первом ее участке равна 25 Å/мм, а на втором 20 Å/мм?

Задача 348. Вычислить положение водородных линий поглощения Η_β, Η_δ и Н_x в спектрах звезд, лучевая скорость одной из которых относительно Земли равна —50 км/с, а другой +30 км/с. Нормальная длина волны этих линий соответственно 4861, 4102 и 3750 Å.

Задача 349. Звезды β Дракона и γ Дракона находятся вблизи северного полюса эклиптики. Линии железа с λ=5168 Å и λ=4384 Å в спектре первой звезды смещены к фиолетовому концу на 0,34Å и 0,29Å, а в спектре второй звезды — на 0,47 Å и 0,40 Å. Определить лучевую скорость этих звезд.

Задача 350. Найти лучевую скорость звезды Канопуса (а Киля), если в ночь наблюдений эклиптическая долгота Солнца была близкой к эклиптической долготе звезды, а линии поглощения железа Ε (5270 Å) и G (4326 Å) в спектрограмме звезды сдвинуты к красному концу соответственно на 0,018 мм и 0,020 мм, при дисперсии 20 Å/мм на первом участке спектрограммы и 15 Å/мм на втором ее участке.

Задача 351. В ночь фотографирования спектра звезды Беги (а Лиры) ее эклиптическая долгота отличалась от эклиптической долготы Солнца на 180°, и линии поглощения водорода Н_β (4861 Å) и Н_γ (4102 Å) оказались сдвинутыми к фиолетовому концу спектрограммы соответственно на 0,0225 мм и 0,0380 мм при дисперсии на участках расположения этих линий равной 10 Å/мм й 5 Å/мм. Найти лучевую скорость Веги.

Задача 352. При каких условиях поправка приведения лучевой скорости звезд к Солнцу равна нулю и при каких её абсолютное значение становится наибольшим?

Звезда	Склонение	Годичный параллакс	Компоненты собственного движения
			по α	по δ
α Близнецов	+32° 00'	0",072	-0^с,0130	—0",110
γ Близнецов	+ 16 27	0,031	+0,0033	-0,046
ρ Близнецов	+31 53	0,059	+0,0121	+0,154
β Гончих Псов	+41 38	0,108	-0,0629	+0,284

Задача 353. По приведенным в таблице сведениям вычислить величину и позиционный угол тангенциальной скорости звезд.

Задача 354. Вычислить тангенциальную скорость звезд, параллакс и собственное движение которых указаны после их названий: Альтаир (а Орла) 0",198 и 0",658; Спика (а Девы) 0",021 и 0",054; ε Индейца 0",285 и 4",69.

Задача 355. Для звезд предыдущей задачи найти компоненты собственного движения по экваториальным координатам. Позиционный угол собственного движения и склонение каждой звезды указаны после ее названия: Альтаир 54°,4 и +8°44'; Спика 229°,5 и —10°54'; ε Индейца 123°,0 и —57°00'.

Задача 356. За какой интервал времени и в каком направлении звезды предыдущей задачи сместятся на диаметр лунного диска (30') и какими будут тогда их экваториальные координаты в координатной сетке 1950.0, если в настоящее время в этой же сетке их координаты: у Альтаира 19ч48м20с,6 и +8°44'05", у Спики 13ч22м33с,3 и —10°54'04" и у ε Индейца 21ч59м33с,0 и — 56°59'34"?

Задача 357. Какими будут экваториальные координаты звезд предыдущей задачи в 2000 г. в координатной сетке этого года, если в местах их положения годовая прецессия по прямому восхождению и по склонению (в последовательности перечисления звезд) равна +2с,88 и +9",1; +3с,16 и —18",7; +4с,10 и +17",4?

Задача 358. Лучевая скорость звезды Ахернара (а Эридана) равна +19 км/с, годичный параллакс 0",032 и собственное движение 0",098, а у звезды Денеба (а Лебедя) аналогичные величины равны соответственно — 5 км/с, 0"",004 и 0",003. Найти величину и направление пространственной скорости этих звезд.

Задача 359. В спектре звезды Проциона (а Малого Пса) линии поглощения железа с длиной волны 5168 Å и 4326 Å смещены (с учетом скорости Земли) к фиолетовому концу соответственно на 0,052 Å и 0,043 Å. Компоненты собственного движения звезды равны— 0c,0473 по прямому восхождению и —1",032 по склонению, а ее параллакс 0",288, Найти величину и направление пространственной скорости Проциона, склонение которого +5°29'.

Задача 360. На спектрограмме звезды Капеллы (а Возничего) линии поглощения железа с длиной волны 4958 Å и 4308 Å сдвинуты к красному концу на 0,015 мм при дисперсии на этих участках соответственно 50 Å/мм и 44 Å/мм. Склонение звезды +45°58', эклиптическая долгота 8l°10', эклиптическая широта +22°52', параллакс 0",073, а компоненты собственного движения + 0^с,0083 и —0",427. В ночь наблюдений эклиптическая долгота Солнца была 46°18/. Узнать величину и направление пространственной скорости звезды.

Задача 361. В настоящую эпоху визуальный блеск звезды Беги (а Лиры) + 0m,14, ее собственное движение 0",345, параллакс 0",123 и лучевая скорость—14 км/с. Найти эпоху наибольшего сближения Веги с Солнцем и вычислить для нее расстояние, параллакс, собственное движение, лучевую и тангенциальную скорость и блеск этой звезды.

Задача 362. Решить предыдущую задачу для звезды Толима-на (а Центавра), визуальный блеск которой в современную эпоху равен +0m,06, собственное движение 3",674, параллакс 0",751 и лучевая скорость — 25 км/с. Какими были искомые величины 10 тыс. лет назад и какими они будут через 10 тыс. лет после эпохи наибольшего сближения?

Задача 363. В спектрах далеких галактик и квазаров наблюдается смещение линий к красному концу (красное смещение). Если это явление интерпретировать как эффект Допплера, то какой лучевой скоростью обладают названные объекты при красном смещении, составляющем соответственно 0,1, 0,5 и 2 длины волны спектральных линий?

Задача 364. По данным предыдущей задачи вычислить расстояния тех же объектов в двух космологических моделях, приняв постоянную Хаббла равной 50 км/с Мпс.

Задача 365. Найти красное смещение в спектрах внегалактических объектов, соответствующее лучевой скорости, равной 0,25 и 0,75 скорости света.

Задача 366. Какое получится различие в лучевых скоростях объектов предыдущей задачи, если вместо релятивистской формулы эффекта Допплера использовать обычную формулу этого эффекта?

Задача 367. В таблице приведены сведения о трех галактиках:

Обозначение галактики	Созвездие	Видимые размеры	Видимая звездная величина	Смещение спектральных линий Η и К
М101 М96 М83	Б.Медведица Лев Волосы Вероники	28'х28' 11 Χ 8 9X6	8m,2 10,0 10,1	6.9Å 10,3 15,8

Зная, что у линий Η и К ионизованного кальция длина волны 3968 Å (Н) и 3934 Å (К), вычислить лучевую скорость, расстояние, линейные размеры, абсолютную звездную величину и светимость этих галактик.

Задача 368. В спектре квазара СТА102, имеющего блеск 17m,3, смещение эмиссионных линий превышает соответствующую длину волны в 1,037 раза, а в спектре квазара PKS 0237—23 (блеск 16m,6) —в 2,223 раза. На каких расстояниях находятся эти квазары и чему равна их светимость? Задачу решить по двум космологическим моделям.

Задача 369. Вычислить расстояние, линейные размеры и светимость квазара ЗС 48, если его угловой диаметр равен 0",56, блеск 16m,0, а линия λ 2798 ионизованного магния смещена в его спектре до положения λ 3832.

Задача 370. Решить предыдущую задачу для квазара ЗС 273 с угловым диаметром 0",24 и блеском 12m,8, если эмиссионные линии водорода в его спектре сдвинуты:

Ηβ (λ 4861) до λ =5640 Å; Н_γ (λ 4340) до

λ = 5030 Å и Η_δ (λ 4102) до λ = 4760 Å.

Задача 371. У одного из наиболее удаленных квазаров красное смещение составляет 3,53 нормальной длины спектральных линий. Найти лучевую скорость квазара и оценить расстояние до него.

Ответы - Движение звезд и галактик в пространстве