
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основы теоретической астрономии и небесной механикиСодержание книги
Поиск на нашем сайте
Эмпирические законы Кеплера и конфигурации планет Планеты обращаются вокруг Солнца по эллиптическим орбитам, в одном, общем фокусе которых находится Солнце. В первом приближении можно считать, что орбиты больших планет (кроме Плутона) лежат в одной плоскости. Большая полуось α орбиты (рис. 4) определяет размеры, а эксцентриситет е — степень вытянутости орбиты.
Рис. 4. Эллиптическая орбита Радиус-вектор r планеты определяется уравнением эллипса
и меняется в пределах от перигельного расстояния q= СП = α (1—е), (35) когда истинная аномалия θ=0°, до афелийного расстояния Q = CA = α (l+e) (36) при θ =180°. Средним расстоянием планеты от Солнца является большая полуось ее орбиты
Расстояния между планетами и расстояния планет от Солнца обычно выражаются в астрономических единицах (а. е.), но иногда и в километрах из расчета, что 1 а. е. = 149,6·106 км. Звездные, или сидерические, периоды обращения Т1 и Т2 двух планет связаны с их средними расстояниями а1 и а2 от Солнца третьим законом Кеплера
Если Τ дается в годах и а — в астрономических единицах, то, принимая для Земли T0 = 1 год и а0 = 1 а. е., получим для любой планеты Т2 = а3 (39) Средняя орбитальная, или круговая, скорость планеты
всегда выражается в км/с. Так как обычно а задается в астрономических единицах (1 а. е.= 149,6·106 км) и T— в годах (1 год=31,56·106 с), то
Заменив Τ из формулы (39), получим:
средняя продолжительность синодического периода обращения S планеты связана с сидерическим периодом Τ уравнением синодического движения:
для верхних планет
для нижних планет где Т0 — сидерический период обращения Земли, равный 1 звездному году. Средний синодический период обращения позволяет вычислить примерную дату t2 очередного наступления определенной конфигурации планеты по известной дате t1 такой же конфигурации, так как t2 ~ t1 + S. (44) Любые планетные конфигурации и даты их наступления могут быть вычислены по гелиоцентрической долготе l планет, отсчитываемой в плоскости эклиптики от точки весеннего равноденствия γ в прямом направлении, т. е. против вращения часовой стрелки. Пусть в некоторый день года t1 гелиоцентрическая долгота верхней планеты l1 а гелиоцентрическая долгота Земли l01 (рис. 5). Планета за средние сутки проходит по орбите дугу ω = 360°/T (среднее суточное движение планеты), а Земля — дугу ω0=360°/T0 (среднее суточное движение Земли), где Τ и Т0 выражены в средних сутках, причем Т > Т0 и ω < ω0. В день t2 искомой конфигурации гелиоцентрическая долгота планеты
Рис. 5. Гелиоцентрическая долгота
а Земли l02 = l01 + ω0 (t2—t1) = l01+ω·Δt, (46) откуда, обозначив ω0—ω = Δω и (l02—l01) — (l2—l1) = L, получим: Δt=L/Δω (47) и t2 = t1+Δt. (48) При вычислении конфигураций нижних планет Δω = ω—ω0. Наибольшие сближения с Землей планет, обращающихся по заметно вытянутым орбитам, повторяются через целые числа m и n средних синодических S и сидерических Τ периодов обращения, поскольку mS = nT. (49) Эта же формула позволяет установить периодичность великих противостояний планет. Пример 1. Найти перигельное и афелийное расстояния, сидерический и синодический периоды обращения, а также круговую скорость малой планеты Поэзии, если большая полуось и эксцентриситет ее орбиты равны 3,12 а. е. и 0,144. Данные: а = 3,12 а.е., е=0,144. Решение. По формулам (35) и (36) перигельное расстояние q = а(1—е) =3,12(1—0,144) =2,67 а. е. и афелийное расстояние Q = a(1+e) =3,12(1+0,144) =3,57 а.е. Формула (39) дает сидерический период обращения T = а√а =3,12√3,12; T = 5,51 года, а так как α > α0 = 1 а. е., то планета верхняя и поэтому ее синодический период обращения S вычисляется по формуле (43) при T0=1 году: S =T/(T-1) = 5,51/(5,51-1); S = 1,22 года. Формула (41) дает круговую скорость va=29,8/√a=29,8/√3,12; va= 16.9 км/с. Пример 2. Определить гелиоцентрическую долготу Земли и планет 21 марта, если в этот день Меркурий находился в верхнем соединении с Солнцем, Венера — в наибольшей западной элонгации (Δλ = 47°) и Марс —в противостоянии. Данные: Меркурий, Δλ=0°; Венера, Δλ = 47°; Марс, Δλ = 180°.
Рис. 6. Конфигурации планет
Решение. На чертеже (рис. 6) изображаем орбиты планет концентрическими окружностями с центром в Солнце, из которого проводим луч, показывающий направление на точку весеннего равноденствия γ. Так как 21 марта Солнце с Земли видно в точке весеннего равноденствия γ, то Земля (з) находится в диаметрально противоположной точке своей орбиты, и ее гелиоцентрическая долгота lо = 180°. Меркурий (М) изображаем в верхнем соединении (за Солнцем), и его гелиоцентрическая долгота lм = 0°. Венера (В) находится в наибольшей западной элонгации и поэтому проводим с Земли касательную к орбите Венеры вправо (к западу) ог Солнца. Гелиоцентрическая долгота Венеры lв= 180°+ (90°—Δλ) =270°-47°=223°. У Марса (Мс), находящегося в противостоянии, гелиоцентрическая долгота lМс=180°.
Данные: Меркурий, t1=18.IV.1975 г., Δλ=22°, ω = 4°,09; Земля, ω0=0°,99. Решение. Меркурий движется быстрее Земли (ω>ω0). Изобразим на чертеже (рис. 7) Землю и расположения Меркурия относительно нее в день t1 верхнего соединения (M1) и в день t2 очередной наибольшей западной элонгации (M2). За промежуток времени Δt = t2—t1 Меркурий пройдет дугу L=M1M2 со средним суточным движением Δω = ω—ω0 = 4°,09—0°,99 = 3°,10. Из чертежа видно, что L = 180°+ (90°—Δλ) = 270°—22° = 248°. Тогда, согласно формуле (47), Δt=L/Δω=248°/3°,10=80 сут
Рис. 7. Относительный путь Меркурия и очередная наибольшая западная элонгация Меркурия наступит вблизи t2 = 18.IV.1975 г. + 80 сут = 98.IV.1975 г. или t2 = 7 июля 1975 г. Задача 115. Вычислить перигельное и афелийное расстояния планет Сатурна и Нептуна, если их средние расстояния от Солнца равны 9,54 а. е. и 30,07 а. е.,а эксцентриситеты орбит— 0,054 и 0,008. Задача 116. Какая из двух планет — Нептун (а = 30,07 а.е., e = 0,008) или Плутон (а = 39,52 а. е., е=0,253) — подходит ближе к Солнцу? В скобках даны большая полуось и эксцентриситет орбиты планеты. Задача 117. Найти значения истинной аномалии планеты, при которых ее радиус-вектор равен среднему гелиоцентрическому расстоянию. Задача 118. Найти эксцентриситет орбиты и перигельное расстояние планеты Марса и астероида Адониса, если у Марса большая полуось орбиты равна 1,52 а. е. и наибольшее расстояние от Солнца 1,66 а. е., а у Адониса соответственно 1,97 а. е. и 3,50 а. е. Указать, какая из этих двух планет подходит ближе к Солнцу. Задача 119. На каком среднем и наибольшем гелиоцентрическом расстоянии движутся малые планеты Икар и Симеиза, если у Икара перигельное расстояние и эксцентриситет орбиты равны 0,187 а. е. и 0,827, а у Симеизы — 3,219 а. е. и 0,181? У какой из этих планет радиус-вектор изменяется в больших пределах, абсолютно и относительно? Задача 120. Вычислить периоды обращения вокруг Солнца планеты Венеры и астероида Европы, у которых средние гелиоцентрические расстояния соответственно равны 0,723 а. е. и 3,10 а. е. Задача 121. Определить периоды обращения вокруг Солнца малой планеты Аполлона и кометы Икейи, если обе они проходят вблизи Солнца почти на одинаковых расстояниях, равных у Аполлона 0,645 а. е., а у кометы 0,633 а. е., но их орбиты имеют эксцентриситеты 0,566 и 0,9933 соответственно. Задача 122. Первый спутник планеты Юпитера — Ио обращается вокруг нее за 42ч28м на среднем расстоянии в 421 800 км. С какими периодами обращаются вокруг Юпитера его спутники Европа и Ганимед, большие полуоси орбит которых равны 671,1 тыс. км и 1070 тыс. км? Задача 123. Найти средние расстояние от Сатурна его спутников Мимаса и Реи, обращающихся вокруг планеты с периодами в 22ч37м и 4д,518. Самый крупный спутник планеты — Титан, обращается за 15д,945 по орбите с большой полуосью в 1221 тыс. км Задача 124. Видимое с Земли суточное смещение Солнца по эклиптике в начале января достигает наибольшего значения 61', а в начале июля — наименьшего значения 57'. Вычислить эксцентриситет земной орбиты и указать, какие ее точки Земля проходит в эти дни. Задача 125. Астероид Фортуна сближается с Землей до расстояния в 1,056 а. е., а астероид Офелия — до 1,716 а. е. Их средние гелиоцентрические расстояния соответственно равны 2,442 а. е. и 3,129 а. е. Найти эксцентриситеты орбит этих астероидов, их перигельиое и афелийное расстояния. Орбиту Земли считать окружностью, а наклонениями орбит астероидов (1°,5 и 2°,5) пренебречь. Задача 126. На каких предельных расстояниях от Земли могут находиться планеты Меркурий (а = 0,387 а.е., е = 0,206) и Марс (а =1,524 а. е., е = 0,093)? В скобках даны большая полуось и эксцентриситет орбиты планеты. Эксцентриситетом земной орбиты пренебречь. Задача 127. Найти пределы изменения диаметра солнечного диска с планеты Марс, если при среднем гелиоцентрическом расстоянии планеты он равен 21'03". Эксцентриситет орбиты планеты равен 0,093. Задача 128. Видимый с Земли диаметр солнечного диска в начале января равен 32'35", а в начале июля — 31'31". Вычислить эксцентриситет земной орбиты, перигельное и афелийное расстояния Земли и сравнить влияние эксцентриситета на смену сезонов года с воздействием наклона земной оси, равного 23°27' (расчеты провести для географической широты 0°, 30° и 60°). Задача 129. Чему равна круговая скорость планет Урана и Плутона, среднее расстояние которых от Солнца составляет соответственно 19,19 а, е. и 39,52 а. е.? Задача 130. Найти среднюю орбитальную скорость астероидов Икара (1,078 а. е.), Крымеи (2,774 а. е.) и Нестора (5,237 а. е.). В скобках указано среднее гелиоцентрическое расстояние астероида. Задача 131. При каких значениях истинной аномалии скорость небесного тела, обращающегося по эллиптической орбите, равна его круговой скорости? Задача 132. Астероид Лидия обычно бывает в противостоянии через каждые 469 сут, а астероид Инна — через 447 сут. Во сколько раз эти астероиды в среднем дальше от Солнца, чем Земля? Задача 133. Средний синодический период обращения Меркурия составляет 116 сут и перигельное расстояние 0,307 а. е., Сатурна —378 сут и 9,024 а. е. Вычислить для этих планет сидерический период обращения, большую полуось и эксцентриситет орбиты, афелийное расстояние, наибольшее и наименьшее геоцентрическое расстояние, круговую скорость, а также предельное изменение количества тепла, получаемого ими от Солнца, вследствие эллиптичности орбиты. Земную орбиту принять круговой. Задача 134. Найти примерные даты предыдущей и очередной наибольшей западной элонгации Венеры, если такая же ее конфигурация была 7 ноября 1975 г. Большая полуось орбиты Венеры равна 0,723 а. е. Задача 135. Вычислить весьма приближенные даты двух очередных верхнего и нижнего соединений Меркурия, если предыдущее нижнее соединение планеты произошло 9 октября 1975 г. Звездный период обращения Меркурия равен 88 сут. Задача 136. Определить гелиоцентрическую долготу планет Меркурия и Юпитера 25 сентября 1975 г., если 9 марта этого же года гелиоцентрическая долгота Меркурия была 243°, а Юпитера 359°. Среднее суточное движение Меркурия 4°,09 и Юпитера 5',0. Задача 137. 17 февраля 1975 г. гелиоцентрическая долгота Венеры была равна 26°, а гелиоцентрическая долгота Сатурна 107°. Среднее суточное движение этих планет соответственно равно 1°,602 и 0°,034. Вычислить гелиоцентрическую долготу обеих планет на 17 июля 1975 г. и объяснить причину резкого различия в изменении гелиоцентрической долготы этих планет за один и тот же промежуток времени. Задача 138. 29 марта 1975 г. гелиоцентрическая долгота Земли была равна 187°, Юпитера 1° и Урана 210°. Когда произойдет ближайшее противостояние этих планет, если среднее суточное движение Земли равно 0°,986, Юпитера 4',98 и Урана 0',72? Задача 139. Найти день очередного верхнего соединения Венеры, если 23 апреля 1975 г. ее гелиоцентрическая долгота равнялась 131°, а гелиоцентрическая долгота Земли— 212°. Среднее суточное движение Венеры равно 1°,602, а Земли 0°,986. Задача 140. Определить день очередного нижнего соединения Венеры, если ее наибольшая западная элонгация (Δλ = 47°) произошла 7 ноября 1975 г. Сведения о среднем суточном движении см. в задаче 139. Задача 141. Вычислить день очередной наибольшей восточной элонгации (Δλ = 22°) Меркурия, если его наибольшая западная элонгация (Δλ = 27°) была 6 марта 1975 г. Среднее суточное движение Меркурия равно 4°,092, а Земли 0°,986. Задача 142. Противостояние астероида Ирмы произошло 23 сентября 1976 г., а Лины — 2 декабря 1976 г. Большая полуось орбиты Ирмы равна 2,772, а. е., а орбиты Лины — 3,139 а. е. Когда произойдет ближайшее соединение этих астероидов друг с другом? Задача 143. Чему была равна гелиоцентрическая долгота Земли и планет 23 сентября, когда Меркурий находился в наибольшей западной элонгации (Δλ=28°), Венера— в нижнем соединении, Марс — в соединении и Юпитер— в противостоянии? Задача 144. Определить гелиоцентрическую долготу Земли и планет 22 июня, если в этот день Меркурий находился в нижнем соединении, Венера — в наибольшей восточной элонгации (Δλ=45°), Марс — в противостоянии и Юпитер — в западной квадратуре. Гелиоцентрическое расстояние Юпитера принять равным 5,20 а. е. Задача 145. Сидерический период обращения Меркурия равен 88д, а синодический период—116д. Примерно через сколько времени повторяются наибольшие сближения Меркурия с Землей? Задача 146. У орбиты Марса большая полуось — около 1,52 а. е. и эксцентриситет 0,093, а у орбиты астероида Эрота—1,46 а. е. и 0,222. Через какие промежутки времени происходят великие противостояния этих планет, на какое примерно расстояние они в эти эпохи сближаются с Землей и насколько могут удаляться от нее вне этих эпох? Орбиту Земли принять круговой, наклонением орбит планет пренебречь. Ответы - Эмпирические законы Кеплера и конфигурации планет
|
||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 4309; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.224.105 (0.007 с.) |


 (34)
(34) (37)
(37)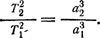 (38)
(38) (40)
(40)



 l2 = l1 + ω(t2- t1) = l1 + ω Δt (45)
l2 = l1 + ω(t2- t1) = l1 + ω Δt (45)
 Пример 3. Верхнее соединение Меркурия произошло 18 апреля 1975 г. Когда примерно наступит ближайшая наибольшая западная элонгация планеты (Δλ=22°), если среднее суточное движение Меркурия ω=4°,09, а Земли ω0=0°,99?
Пример 3. Верхнее соединение Меркурия произошло 18 апреля 1975 г. Когда примерно наступит ближайшая наибольшая западная элонгация планеты (Δλ=22°), если среднее суточное движение Меркурия ω=4°,09, а Земли ω0=0°,99?




