
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основы сферической и практической астрономииСодержание книги
Поиск на нашем сайте
СБОРНИК ЗАДАЧ ПО АСТРОНОМИИ Мы представляем вашему вниманию «Сборник задач по астрономии». На нашем сайте вы найдете теоретическую часть, примеры, упражнения и ответы к ним, подразделенные на 4 основные категории, для удобства пользования сайтом. Данные разделы охватывают: основы сферической и практической астрономии, основы теоретической астрономии и небесной механики, основы астрофизики и характеристики телескопов. Щелкнув курсором мыши в правой части нашего сайта на любом из подразделов в 4 категориях вы обнаружите в каждой из них теоретическую часть, которую мы советуем вам изучить до преступления к непосредственному решению задач, далее вы найдете пункт «Примеры», который мы добавили для лучшего понимания теоретической части, непосредственно сами упражнения для закрепления и расширения ваших знаний в данных областях и также пункт «Ответы» для проверки полученных знаний и коррекции ошибок. Возможно, на первый взгляд, некоторые задачи покажутся устаревшими, так как географические названия стран, районов и городов, упомянутых на сайте, изменились со временем, законы астрономии же не претерпевали никаких изменений. Поэтому по нашему мнению, сборник содержит много полезной информации в теоретических частях, которые содержат неустаревающую информацию, доступную в виде таблиц, графиков, диаграмм и текста. Наш сайт предоставляет вам возможность начать изучение астрономии с азов и продолжить обучение с помощью решения задач. Сборник поможет вам заложить основы увлечения астрономией и может быть, в один день вы откроете новую звезду или полетите к ближайшей планете. ОСНОВЫ СФЕРИЧЕСКОЙ И ПРАКТИЧЕСКОЙ АСТРОНОМИИ Ответы - Кульминация светил. Вид звездного неба
Задача 27 По результатам предыдущей задачи обнаружить закономерность в вычисленных величинах и указать, в каких из трех городов бывают вблизи летнего солнцестояния белые, светлые и темные ночи. Задача 28. Определить отношение количества тепла, получаемого от Солнца в полдень дней равноденствий и солнцестояний городами, указанными в задаче 26. Сравнение провести для каждого города в отдельности (по датам) и по городам в каждую дату. Задача 29. Найти полуденную и полуночную высоту Солнца в дни равноденствий и солнцестояний на земном экваторе, на тропиках, на полярных кругах и географических полюсах. Задача 30. Определить отношение количества тепла, получаемого в полдень дней равноденствий и солнцестояний местами земной поверхности, указанными в предыдущей задаче. Сравнение провести для каждого места (в различные даты) и по местностям (в каждую дату). Задача 31. На каких географических параллелях Солнце не восходит, проходит в зените и не заходит в дни, когда его склонение равно +21°19' и —16°43'? Задача 32. В какие дни года Солнце проходит в зените и надире экватора, тропиков и земных параллелей с географической широтой +7°48' и —18°35'? (Некоторые даты следует установить по астрономическому календарю-ежегоднику.) Задача 33. На какой географической широте Солнце кульминирует в день летнего солнцестояния на зенитном расстоянии в 10°41' к северу от зенита? Чему равна полуденная и полуночная высота Солнца на той же широте в дни равноденствий и солнцестояний? Задача 34. Решить предыдущую задачу при том же полуденном зенитном расстоянии Солнца, но к югу от зенита. Задача 35. Найти планетографическую широту* тропиков и полярных кругов на планетах Марсе, Юпитере и Уране, если наклон оси Марса равен 24°48', оси Юпитера 3°07', а оси Урана 98° (наклон больший 90° означает обратное вращение планеты). * Угловое расстояние от экватора планеты, аналогичное географической широте на Земле. Задача 36. По результатам предыдущей задачи отметить особенности расположения тропиков и полярных кругов в сравнении с земными и определить пределы изменения склонения Солнца в небе этих планет. Задача 37. Вычислить отношение количества тепла, получаемого от Солнца в полдень дней равноденствий и летнего солнцестояния экватором, северным тропиком и северным полярным кругом Урана и выяснить условия освещения различных зон этой планеты на протяжении периода ее обращения вокруг Солнца, близкого к 84 годам. Наклон оси планеты равен 98°. Задача 38. При каком склонении Солнца наступают белые ночи в Ленинграде (ср = +59°57') и Архангельске (φ= +64°34')? Возможны ли в этих городах полярные дни и полярные ночи? Задача 39. По результатам предыдущей задачи и астрономическому календарю-ежегоднику определить длительность периода белых ночей в тех же городах. Задача 40. Воспользовавшись астрономическим календарем-ежегодником, найти длительность периода белых ночей и продолжительность полярного дня и полярной ночи в Мурманске (φ = +68°59') и Хатанге (φ = +71°58') и определить наибольшую полуденную и полуночную высоту Солнца в этих городах. Задача 41. До каких географических параллелей распространяются границы полярного дня, полярной ночи, белых и темных ночей в дни равноденствий и солнцестояний? Задача 42. На каких географических параллелях начинаются и оканчиваются периоды белых ночей, полярный день и полярная ночь при склонениях Солнца δ = +10° и δ = = +21°? Примерно в какие дни года это происходит? Ответы - Видимое годовое движение Солнца
Системы счета времени Звездное время S измеряется часовым углом tγ точки весеннего равноденствия и поэтому всегда S = tγ У небесного светила с прямым восхождением α часовой угол t = S—α. (13) Звездное время S в пункте с географической долготой λ связано со звездным гринвичским временем S0 равенством S = S0+λ, (14) причем λ отсчитывается к востоку от Гринвича и выражается в часах, минутах и секундах времени. Для перевода градусных единиц в единицы времени существуют таблицы. В один и тот же физический момент звездное время S1 и S2 в двух пунктах различается на разность географической долготы λ1 и λ2 этих пунктов, т. е. S2—S1=λ2—λ1. (15) Используемые в практической жизни средние солнечные сутки продолжительнее звездных суток на 3м56с,6 ~ Зм56с. Местное среднее время Tλ =T где η — уравнение времени, a T Τ Местное среднее время Tλ1 и Tλ2 двух пунктов связано между собой равенством: Tλ1 - Tλ2 = λ2—λ1, (18) а со средним гринвичским временем T0 (называемым всемирным временем)—равенством Тλ = T0+λ. (19) В практической жизни используется либо поясное время Tn = T0+n, (20) либо декретное время Tд = Tn + 1ч=T0+n+1ч, (21) где n — номер часового пояса, равный целому числу часов. Для двух пунктов, расположенных в разных часовых поясах n1 и n2, Tд2 —Tд1 = Τn2 -Тn1 =n2-n1 (22) Если система счета времени не указана, то всегда подразумевается время, действующее на данной территории. Показание часов Тч (или Sч) не всегда соответствует моменту точного времени Τ или S. Разность u = Т—Тч или us=S — Sч (23) называется поправкой часов, зная которую можно определять точное время по неверно идущим часам. Пример 1. Определить звездное время в пунктах с географической долготой 2ч23м37с и 7ч46м20с в момент, когда в пункте с географической долготой 80°05',5 у звезды Веги (α Лиры) часовой угол равен 4ч29м48с. Прямое восхождение Веги α=18ч35м15с. Данные: λ1 = 2ч23м37c; λ2=7ч46м20с; λ3 = 80°05',5; Вега, α=18ч35м15с, t = 4ч29м48c. Решение. Пользуясь таблицей 2, выражаем географическую долготу третьего пункта в единицах времени: λ3=80°05',5 = 5ч20м22с. Согласно формуле (13), звездное время в третьем пункте (с λ3) S3=α+t = 18ч35м15c+4ч29м48c=23ч05м03c. Из формулы (15) следует, что в первом пункте (с λ1) звездное время S1=S3+(λ1-λ3) - 23ч05м03с + (2ч23м37с—5ч20м22с) = 20ч08м18с; во втором пункте (с λ2) звездное время S2 = S3+ (λ2—λ3) =23ч05м03с+ (7ч46м20с—5ч20м22с) = 25ч31м01с, т. е. в этом пункте начались уже новые звездные сутки (но не календарные сутки), и там S2=1ч31м01c. При другом ходе решения используется формула (14). Пример 2. Некоторый пункт с географической долготой 5ч34м находится в пятом часовом поясе. Найти местное среднее, поясное и декретное время этого пункта в истинный полдень 27 октября, если в этот день уравнение времени равно —16м. Данные: λ=5ч34м, n=5; 27 октября η = —16м. Решение. В истинный полдень истинное солнечное время T Τλ =T Tn = Tλ + (n—λ) = 11ч44м—34м=11ч10м и декретное время Tд=Tn+1ч=12ч10м Задача 43. Определить звездное время в моменты верхней и нижней кульминации звезды Фомальгаута (α Южной Рыбы), прямое восхождение которой 22ч54м53с. Задача 44. Найти звездное время в моменты, в которые часовой угол звезды Ригеля (β Ориона) соответственно равен —3ч17м43с и 1ч42м29с. Прямое восхождение этой звезды 5ч12м08с Задача 45. Определить звездное время в пунктах с географической долготой 2ч13м23с и 84°58' в момент, когда в пункте с долготой 4ч37м11с звезда Кастор (α Близнецов) находится в верхней кульминации. Прямое восхождение Кастора 7ч31м25с. Задача 46. Решить предыдущую задачу для тех же пунктов, но для момента времени, в который звезда Капелла (а Возничего) находится в нижней кульминации в Иркутске (λ=6ч57м05с). Прямое восхождение Капеллы 5ч13м00с. Задача 47. Вычислить часовые углы звезд Алголя (β Персея) и Альтаира (а Орла) в 8ч20м30с по звездному времени. Прямое восхождение этих звезд соответственно равно 3ч04м54с и 19ч48м21с. Часовые углы выразить в градусных единицах. Задача 48. Прямое восхождение звезды Миры (о Кита) 2ч16м49с, Сириуса (а Большого Пса) 6ч42м57с и Проциона (а Малого Пса) 7ч36м41с. Чему равны часовые углы этих звезд в моменты верхней и нижней кульминации Сириуса? Задача 49. Найти часовые углы звезд Кастора (а Близнецов) и Шеата (β Пегаса) в момент, когда часовой угол звезды Беги (а Лиры) равен 4ч15м10с. Прямое восхождение Кастора 7ч31м25с, Беги 18ч35м15с и Шеата 23ч01м21с. Задача 50. Часовой угол звезды Миры (о Кита) в Гринвиче равен 2ч16м47с. Определить в этот момент звездное время в пунктах с географической долготой 2ч03м02с и 54°44',5. Прямое восхождение Миры 2ч16м49с. Задача 51. Найти звездное время и часовой угол звезды Мицара (ζ Большой Медведицы) в Гринвиче и в пункте с географической долготой 6ч34м09с в тот момент, когда в Якутске (λ=8ч38м58с) часовой угол звезды Альдебарана (а Тельца) 329°44'. Прямое восхождение Мицара 13ч21м55с, а Альдебарана 4ч33м03с. Задача 52. Какое прямое восхождение у звезд, находящихся в верхней и нижней кульминации в двух различных пунктах наблюдения, если в одном из них, расположенном восточнее другого на 36°42', часовой угол звезды Проциона (а Малого Пса) равен —2ч16м41с? Прямое восхождение Проциона 7ч36м41с. Задача 53. На каких географических меридианах звездное время соответственно равно 22ч48м30с и 7ч36м34с, если в местности с географической долготой 5ч31м40с звезда Задача 54. Через какие интервалы звездного времени после верхней кульминации звезды β Льва с прямым восхождением 11ч46м31с звезда α Гидры будет находиться в верхней кульминации, в нижней кульминации и занимать положение при часовом угле 4ч25м16с? Прямое восхождение α Гидры 9ч25м08с. Задача 55. В момент верхней кульминации звезды Геммы (а Северной Короны), прямое восхождение которой 15ч32м34с, часы, идущие по звездному времени (звездные часы), показывали 15ч29м42с. Найти поправку часов и их показание при часовом угле той же звезды, равном 1ч20м50с. Задача 56. В момент верхней кульминации звезды Альдебарана (а Тельца) с прямым восхождением 4ч33м03с звездные часы показывали 4ч52м16с, а в такой же момент следующей ночи их показание было 4ч51м04с. Вычислить поправки звездных часов в моменты наблюдений, а также их суточный и часовой ход (т. е. изменение поправки за сутки и за один час). Задача 57. В момент верхней кульминации звезды ε Большой Медведицы с прямым восхождением 12ч51м50с звездные часы показывай 12ч41м28с, а в момент последующей нижней кульминации той же звезды их показание было 0ч41м04с. При каких показаниях тех же часов звезда β Малой Медведицы проходила обе кульминации, если, ее прямое восхождение равно 14ч50м50с? Задача 58. Найти среднее, поясное и декретное время в пунктах с географической долготой 4ч43м28с и 9ч18м37с в момент 6ч52м06с по среднему гринвичскому времени. Первый пункт находится в пятом, а второй — в десятом часовом поясе. Задача 59. Определить среднее, поясное и декретное время в пунктах с географической долготой 5ч12м56с и 7ч51м22c если в этот момент в третьем пункте часы показывали 17ч31м44с по среднему времени, а географическая долгота третьего пункта равна 6ч27м36с. Первый пункт находится в пятом, а второй — в восьмом часовом поясе. Задача 60. Найти разность между поясным и средним, а также между декретным и средним временем в пункте с географической долготой 7ч18м58с, расположенном в седьмом часовом поясе. Задача 61. Определить последовательность наступления одноименных моментов по среднему, поясному и декретному времени в Баку (λ=3ч19м, n=3) и Новосибирске (λ=5ч32м, n=6). Задача 62. В какие моменты времени по различным системам счета наступают истинный полдень и истинная полночь в Ростове-на-Дону (λ=2ч39м, n=3) и Оренбурге (λ=3ч41м, n=4) в дни, когда уравнение времени соответственно равно +12м и —15м? Задача 63. Точные городские часы Красноярска (n = 6) показывают 7ч32м вечера. Какое в этот момент среднее, поясное и декретное время в Киеве (λ=2ч02м, n=2) и Хабаровске (λ=9ч00м, n=9)? Задача 64. После месячного полета на научной космической станции «Салют-4» космонавты А. А. Губарев и Г. М. Гречко 9 февраля 1975 г. в 14ч03м по московскому времени приземлились северо-восточнее Целинограда. Сколько времени было в этот момент в Целинограде (n = 5) и Казани (n=3)? Москва находится во втором часовом поясе. Задача 65. Лунное затмение 18 ноября 1975 г. началось в 20ч38м,5 и окончилось 19 ноября 1975 г, в 0ч08м,2 по всемирному времени. В какие даты и моменты времени оно началось и окончилось в Краснодаре (n=3), Ташкенте (n = 5) и Иркутске (n = 7)? Задача 66. В 1974 г. летнее солнцестояние наступило 21 июня в 18ч38м по всемирному времени. Когда оно наступило по времени городов, указанных в предыдущей задаче? Задача 67. В момент передачи из Москвы (n = 2) 12-часового радиосигнала точного времени часы в одном из учреждений Томска (λ=5ч40м, n = 6) показывали 16ч12м. Вычислить поправку этих часов к местному среднему и принятому времени Томска и Красноводска (λ=3ч32м, n=4) и найти показания тех же часов в 19ч0м по времени каждого города. Задача 68. Самолет вылетел из Свердловска (n = 4) в 11ч20м и прибыл без опоздания в Иркутск (n = 7) в 17ч45м. Сколько времени летел самолет и какие моменты вылета и прибытия указаны в расписании Аэрофлота? Задача 69. Телеграмма отправлена из Нерчинска (n = 8) в 7ч40м вечера по городским часам и доставлена адресату в Смоленске (n=2) в тот же день в 16ч20м по времени этого города. Сколько времени шла телеграмма и какие моменты времени отправки и доставки отмечены на ней? Ответы - Системы счета времени
Ответы - Практическое определение географических и небесных экваториальных координат
Преобразование небесных координат и систем счета времени. Восход и заход светил Связь между горизонтальными и экваториальными небесными координатами осуществляется через параллактический треугольник PZM (рис. 3), вершинами которого служат полюс мира Р, зенит Ζ и светило M, а сторонами — дуга ΡΖ небесного меридиана, дуга ΖΜ круга высоты светила и дуга РМ его круга склонения. Оче видно, что ΡΖ=90°—φ, ZM = z = 90°—h и PM=90°—δ, где φ — географическая широта места наблюдения, z — зенитное расстояние, h — высота и δ — склонение светила. В параллактическом треугольнике угол при зените равен 180°—A, где A — азимут светила, а угол при полюсе мира — часовому углу t того же светила. Тогда горизонтальные координаты вычисляются по формулам
sin z · cos A = - sin δ · cos φ+cos δ · sin φ · cos t, (29) sin z · sin A = cos δ · sin t, (30) а экваториальные координаты — по формулам sin δ = cos z · sin φ — sin z · cos φ · cos A, (31) cos δ · cos t = cos z · cos φ+sin z · sin φ · cos A, (32) cos δ · sin t=sin z · sin A, (30) причем t = S — α, где α — прямое восхождение светила и S — звездное время.
Рис. 3. Параллактический треугольник
При расчетах необходимо по таблице 3 переводить интервалы звездного времени ΔS в интервалы среднего времени ΔT (или наоборот), а звездное время s0 — в среднюю гринвичскую полночь заданной даты заимствовать из астрономических календарей-ежегодников (в задачах этого раздела значения s0 приводятся). Пусть некоторое явление в каком-то пункте земной поверхности произошло в момент Τ по принятому там времени. В зависимости от принятой системы счета времени по формулам (19), (20) или (21) находится среднее гринвичское время T0, представляющее собой интервал среднего времени ΔT, протекший с гринвичской полночи (ΔT=T0). Этот интервал по таблице 3 переводится в интервал звездного времени ΔS (т. е. ΔT→ΔS), и тогда в заданный момент T соответствующий среднему гринвичскому времени T0, звездное время в Гринвиче S0=s0+ΔS, (33) а в данном пункте S = S0+λ, (14) где λ — географическая долгота места, Перевод интервалов звездного времени ΔS в интервалы среднего времени ΔΤ = Τ0 (т. е. ΔS→ΔT) осуществляется по таблице 3 вычитанием поправки. Моменты времени и азимуты точек восхода и захода светил вычисляются по формулам (28), (29), (30) и (13), в которых принимается z=90°35' (с учетом рефракции ρ = 35'). Найденные значения часового угла и азимута в пределах от 180 до 360° соответствуют восходу светила, а в пределах от 0 до 180° — его заходу. При вычислениях восхода и захода Солнца учитывается еще его угловой радиус r=16'. Найденные часовые углы t Моменты восхода и захода всех светил вычисляются с точностью, не превышающей 1м. Преобразование небесных координат и систем счета времени – Пример 1 В каком направлении был заранее установлен телескоп с фотокамерой для фотографирования солнечного затмения 29 апреля 1976 г., если в пункте с географическими координатами λ=2ч58м,0 и φ = +40°14' середина затмения наступила в 15ч29м,8 по времени, отличающемуся от московского на +1ч? В этот момент экваториальные координаты Солнца: прямое восхождение α=2ч27м,5 и склонение δ= + 14°35'. В среднюю гринвичскую полночь 29 апреля 1976 г. звездное время s0=14ч28м19c. Данные: пункт наблюдения, λ = 2ч58м,0, φ = +40°14', T=15ч29м,8, Τ—Tм=1ч; s0 = 14ч28м19c = 14ч28м,3; Солнце, α=2ч27м,5, δ = +14°35'. Решение. В середине затмения московское время Тм = Т—1ч=14ч29м,8, и поэтому среднее гринвичское время T0 = Tм—3ч = 11ч29м,8. С гринвичской полночи прошел интервал времени ΔТ = Т0 = 11ч29м,8, который переводим по таблице 3 в интервал звездного времени ΔS=11ч31м,7, и тогда в момент T0, по формуле (33), звездное время в Гринвиче S0=s0+ΔS = 14ч28м,3 + 11ч31м,7 = 25ч60м = = 2ч0м,0 а в заданном пункте, по формуле (14), звездное время S = S0+λ=2ч0м,0 + 2ч58м,0 = 4ч58м,0 и, по формуле (13), часовой угол Солнца t = S—α = 4ч58м, 0—2ч27м, 5 = 2ч30м, 5, или, переводя по таблице 1, t = 37°37',5 ~ 37°38'. По таблицам тригонометрических функций находим: sin φ = sin 40°14' = +0,6459, cos φ = cos 40°14' = +0,7634; sin δ = sin 14°35' = +0,2518, cos δ = cos 14°35' = +0,9678; sin t = sin 37°38' = +0,6106, cos t = cos 37°38' = +0,7919. По формуле (28) вычисляем cos z = 0,6459 · 0,2518 + 0,7634 · 0,9678 · 0,7919 = = +0,7477 и по таблицам находим z = 41°36' и sin z = +0,6640. Для вычисления азимута используем формулу (30):
откуда получаем два значения: A = 62°52' и A = 180° — 62°52' = 117°08'. При δ<φ значения A и t не слишком резко отличаются друг от друга и поэтому A=62°52'. Следовательно, телескоп был направлен в точку неба с горизонтальными координатами A=62°52' и z = 41°36' (или h = + 48°24'). Преобразование небесных координат и систем счета времени - Пример 2 Вычислить азимуты точек и моменты восхода и захода Солнца, а также продолжительность дня и ночи 21 июня 1975 г. в местности с географическими координатами λ=4ч28м,4 и φ = +59°30', находящейся в пятом часовом поясе, если в полдень этого дня склонение Солнца δ = +23°27', а уравнение времени η = + 1м35с. Данные: Солнце, δ = +23°27'; η = +1м35с = +1м,6; место, λ=4ч28м,4, φ = 59°30', n = 5. Решение. Учитывая среднюю рефракцию в горизонте ρ = 35' и угловой радиус солнечного диска r =16', находим, что в момент восхода и захода Солнца центр солнечного диска находится под горизонтом, на зенитном расстоянии z = 90° + ρ + r = 90°51', Тогда sin z = +0,9999, cos z = -0,0148, sin δ = + 0,3979, cos δ = +0,9174, sin φ = +0,8616, cos φ = +0,5075. По формуле (28) находим:
и по таблицам t = ± (180°—39°49',3) = ±140°10',7 и sin t = ±0,6404. По таблице 2 получим, что при восходе Солнца его часовой угол t1 = -140°10',7 = -9ч20м,7, а при заходе t2 = +140°10',7 = +9ч20м,7, т. е. по истинному солнечному времени, согласно формуле (17), Солнце восходит в T и заходит в T что, по формуле (16), соответствует моментам по сред нему времени Tλ1 = T Τλ2 = T По формулам (19), (20) и (21) те же моменты по поясному времени: восход Tn1 = Tλ1— λ+n = 2ч41м — 4ч28м + 5ч = 3ч13м и заход Tn2 = Tλ2 — λ+n = 21ч22м — 4ч28м + 5ч = 21ч54м, а по декретному времени: восход Tд1=4ч13м и заход Tд2 = 22ч54м. Продолжительность дня τ = Тд2—Тд1 = 22ч54м—4ч13м = 18ч41м. В момент нижней кульминации высота Солнца hн = δ— (90°—φ) = +23°27' - (90°—59°30') = -7°03', т. е. вместо обычной длится белая ночь. Азимуты точек восхода и захода Солнца вычисляются по формуле (30):
что дает A = ±(180°—36°,0) = ±144°,0, так как азимуты и часовые углы Солнца находятся в одном квадранте. Следовательно, Солнце восходит в точке истинного горизонта с азимутом A1 = -144°,0 = 216°,0 и заходит в точке с азимутом A2 = +144°,0, расположенных в 36° по обе стороны от точки севера. Задача 90. Через какие интервалы среднего времени чередуются одноименные и разноименные кульминации звезд? Задача 91. Через сколько времени после верхней кульминации Денеба наступит верхняя кульминация звезды γ Ориона, а затем — снова верхняя кульминация Денеба? Прямое восхождение Денеба 20ч39м44с, а γ Ориона 5ч22м27с. Искомые интервалы выразить в системах звездного и среднего времени. Задача 92. В 14ч15м10с по среднему времени звезда Сириус (α Большого Пса) с прямым восхождением 6ч42м57с находилась в нижней кульминации. В какие ближайшие моменты времени после этого звезда Гемма (α Северной Короны) будет находиться в верхней кульминации и когда ее часовой угол будет равен 3ч16м0с? Прямое восхождение Геммы 15ч32м34с. Задача 93. В 4ч25м0с часовой угол звезды с прямым восхождением 2ч12м30с был равен —34°26',0. Найти прямое восхождение звезд, которые в 21ч50м0с будут находиться в верхней кульминации и в нижней кульминации, а также тех звезд, часовые углы которых станут равными — 1ч13м20с и 5ч42м50с. Задача 94. Чему равно приближенное значение звездного времени в среднюю, поясную и декретную полночь Ижевска (λ = 3ч33м, n = 3) 8 февраля и 1 сентября? Задача 95. Примерно в какие дни года звезды Сириус (α = 6ч43м) и Антарес (α = 16ч26м) находятся в верхней и нижней кульминации в среднюю полночь? Задача 96. Определить звездное время в Гринвиче в 7ч28м16с 9 января (s0 = 7ч11м39c)* и в 20ч53м47с 25 июля (s0 = 20ч08м20с). * Здесь и далее в скобках после дат указано звездное время в среднюю гринвичскую полночь. Задача 97. Найти звездное время в средний, поясной и декретный полдень, а также в среднюю, поясную и декретную полночь в Москве (λ = 2ч30м17с, n=2) 15 января (s0=7ч35м18c).* * Здесь и далее в скобках после дат указано звездное время в среднюю гринвичскую полночь. Задача 98. Решить предыдущую задачу для Красноярска (λ = 6ч11м26с, n = 6) и Охотска (λ = 9ч33м10с, n=10) в день 8 августа (s0=21ч03м32c). Задача 99. Вычислить часовые углы звезды Деиеба (α Лебедя) (α = 20ч39м44с) в Гринвиче в 19ч42м10с 16 июня (S0=17ч34м34с) и 16 декабря (S0=5ч36м04c). Задача 100. Вычислить часовые углы звезд α Андромеды (α = 0ч05м48с) и β Льва (α= 11ч46м31с) в 20ч32м50с 3 августа (s0=20ч43M40c) и 5 декабря (s0=4ч52M42c) во Владивостоке (λ=8ч47м31с, n = 9). Задача 101. Найти часовые углы звезд Бетельгейзе (α = 5ч52м28с) и Спики (α =13ч22м33с) в 1ч52м36с 25 июня (s0=18ч06м07c) и 7 ноября (s0=2ч58м22c) в Ташкенте (λ=4ч37м11с, n=5). Задача 102. В какие моменты времени в Гринвиче находятся в верхней кульминации звезда Поллукс (α = 7ч42м16с), а в нижней кульминации звезда Арктур (α =14ч13м23с) 10 февраля (s0=9ч17м48c) и 9 мая (s0=15ч04м45c)? Задача 103. Найти моменты верхней и нижней кульминации 22 марта (s0 = 11ч55м31c) и 22 июня (s0 = 17ч58м14c) звезд Капеллы (α = 5ч13м00с) и Беги (α = 18ч35м15с) на географическом меридиане λ = 3ч10м0с (n = 3). Моменты указать по звездному, среднему, поясному и декретному времени. Задача 104. В какие моменты времени 5 февраля (s0 = 8ч58м06с) и 15 августа (s0 = 21ч31м08c) часовые углы звезд Сириуса (α = 6ч42м57с) и Альтаира (α = 19ч48м21с) в Самарканде (λ = 4ч27м53с, n = 4) равны 3ч28м47с? Задача 105. В какие моменты времени 10 декабря (s0 =5ч12м24с) часовые углы звезд Альдебарана (α = 4ч33м03с) и β Лебедя (α = 19ч28м42с) в Тбилиси (λ = 2ч59м11с, n = 3) и в Охотске (λ = 9ч33м10с, n=10) соответственно равны +67°48' и —24°32'? Задача 106. На каких географических меридианах звезды α Близнецов и γ Большой Медведицы находятся в верхней кульминации 20 сентября (s0=23ч53м04c) в 8ч40м26с по времени Иркутска (n=7)? Прямое восхождение этих звезд соответственно равно 7ч31м25с и 11ч51м13с. Задача 107. Определить горизонтальные координаты звезд ε Большой Медведицы (а = 12ч51м50с, δ = +56°14') и Антареса (α = 16ч26м20с, δ = -26°19') в 14ч10м0с по звездному времени в Евпатории (φ = +45°12'). Задача 108. Чему равны горизонтальные координаты звезд Геммы (α = 15ч32м34с, δ = +26°53') и Спики (α = 13ч22м33с, δ = —10°54') 15 апреля (s0 = 13ч30м08c) и 20 августа (s0 = 21ч50м50c) в 21ч30м по декретному времени в пункте с географическими координатами λ = 6ч50м0с (n = 7) и φ = +71°58'? Задача 109. В какие точки неба, определяемые горизонтальными координатами, необходимо направить телескоп, установленный в пункте с географическими координатами λ = 2ч59м,2 (n = 3) и φ = +41°42', чтобы 4 мая 1975 г. (s0=14ч45м02с) в 22ч40м по поясному времени увидеть Уран (α = 13ч52м,1, δ = —10°55') и Нептун (α = 16ч39м,3, δ = -20с32')? Задача 110. В какие моменты времени восходит, кульминирует и заходит и сколько времени находится над горизонтом точка летнего солнцестояния 22 марта (s0 = 11ч55м31с) и 22 июня (s0=17ч58м14c) на центральном меридиане второго часового пояса в местах с географической широтой φ = +37°45' и φ = +68°20'? Моменты выразить по звездному и декретному времени. Задача 111. Вычислить азимуты и моменты восхода, верхней кульминации, захода и нижней кульминации звезд Кастора (α = 7ч31м25с, δ = +32°00') и Антареса (α = 16ч26м20с, δ = —26°19') 15 апреля (s0=13ч30м08c) и 15 октября (s0=1ч31м37c) в местах земной поверхности с географическими координатами λ =3ч53м33с (n = 4), φ = +37°45' и λ = 2ч12м15с (n = 2), φ = +68°59'. Задача 112. Вычислить азимуты и моменты восхода, верхней кульминации и захода Солнца, его полуденную и полуночную высоту, а также продолжительность дня в даты весеннего равноденствия и обоих солнцестояний в пунктах с географическими координатами λ = 2ч36м,3 (n=2), φ = +59°57', и λ = 5ч53м,9 (n = 6), φ = +69°18'. В последовательные даты уравнение времени соответственно равно +7м23с, +1м35с и —2м08с. Задача 113. В какие моменты времени 30 июля (s0 = 20ч28м03с) в пункте с λ = 2ч58м0с (n=3) и φ = +40°14' нижеперечисленные звезды имеют горизонтальные координаты A и z:
Задача 114. В пункте с географическими координатами λ= 4ч37м11c (n = 5) и φ = + 41°18' 5 августа 1975 г. (s0= 20ч51м42с) были измерены горизонтальные координаты двух звезд: в 21ч10м у первой звезды A = —8°33' и z =49°51', а в 22ч50м у второй звезды A = 46°07' и z = 38°24'. Вычислить экваториальные координаты этих звезд. Ответы - Преобразование небесных координат и систем счета времени
Ответы - Расстояния, размеры и вращение тел Солнечной системы
Ответы - Закон всемирного тяготения и задача двух тел
Искусственные небесные тела При запуске искусственных небесных тел им сообщается начальная скорость (скорость запуска) vн зависящая от рассчитанной орбиты. Начальная скорость сообщается космическим двигателем на некоторой высоте hн над поверхностью центрального тела (вокруг которого запускается спутник), г. е. от его центра на расстоянии r=R+hн, (74) где R — средний радиус этого тела. В частности, при запуске вокруг Земли R = 6371 км ~ 6370 км, что следует иметь в виду при решении задач этого раздела. Форма и размеры эллиптической орбиты искусственного спутника определяются целями запуска (рис. 8).
Рис. 8. Эллиптическая орбита искусственного спутника Центр центрального тела является одним из фокусов орбиты, а ее большая полуось
причем перицентрическое расстояние q = R+hq (76) и апоцентрическое расстояние Q = R+hQ, (77) где hq — наименьшая высота (высота перицентра) и hQ — наибольшая высота (высота апоцентра) искусственного спутника над поверхностью тела. Для искусственных спутников и орбитальных кораблей Земли hq — высота перигея, hQ — высота апогея, q — перигейное расстояние и Q — апогейное расстояние. Эксцентриситет орбиты определяется формулой (35). Скорость искусственных небесных тел обычно выражается в км/с и вычисляется по формулам (40), (64) — (66) и (68) — (70). Периоды обращения искусственных спутников принято измерять в минутах, а их расстояния—в километрах, и поэтому третий закон Кеплера имеет вид
или
и
где M — масса центрального тела, выраженная в массах Земли. По параметрам обращения искусственного спутника можно вычислить массу центрального тела. Продолжительность полета искусственных спутников над полушарием центрального тела, расположенным под перицентром орбиты (перицентрийное полушарие),
где Τ — период обращения спутника и е — эксцентриситет его орбиты. Над противоположным (апоцентрийным) полушарием спутник пролетает за интервал времени τ=T—t. (82) Формулы (75) — (82) вполне применимы и к движению естественных спутников планет. В полете с одной планеты к другой межпланетная станция (межпланетный корабль) становится спутником Солнца и движется в его поле тяготения по законам движения планет. Простейшей траекторией полета является полуэллиптическая, вершины (апсиды) которой касаются орбит планеты запуска (с нее производится запуск) и планеты сближения (к ней направляется станция). Пренебрегая в первом приближении наклонением и эллиптичностью планетных орбит, можно проводить расчеты по значениям их больших полуосей a1 (планеты запуска) и a2 (планеты сближения), заданных в астрономических единицах (а. е.). При полете к верхней планете (рис. 9) запуск станции осуществляется на ее перигельном расстоянии q=a1 (83) в прямом направлении; афелийное же расстояние станции Q=a2. (84)
Рис. 9. Простейшая орбита межпланетного корабля При направлении станции к нижней планете q = a2 и Большая полуось а гелиоцентрической орбиты межпланетной станции вычисляется по формуле (37), эксцентриситет орбиты — по формуле (35), а продолжительность полета, выраженная в годах,
где а — в астрономических единицах. При необходимости Δt переводится в сутки. Гелиоцентрическая скорость полета станции дается формулами (41), (64), (65) и (66). При запуске к верхней планете начальная гелиоцентрическая скорость Vн = Vq а при запуске к нижней планете Vн = VQ причем в эту скорость Vн входит орбитальная (в рассматриваемом здесь простейшем случае—круговая) скорость V1 планеты запуска. Следовательно, чтобы межпланетная станция вышла на расчетную гелиоцентрическую орбиту, необходимо сообщить ей дополнительную скорость Vд = Vн - V1 (86) Но, чтобы покинуть планету запуска, станция должна еще преодолеть ее притяжение, на что требуется кинетическая энергия где т — масса станции и wп — вторая космическая (критическая) скорость на поверхности этой планеты. Поэтому скорость запуска vн станции с планеты, называемая также начальной планетоцентрической скоростью, найдется из равенства
откуда
День запуска t1 межпланетной станции не может быть произвольным и выбирается по подходящей конфигурации Δλ2 планеты сближения Ρ (см. рис. 9), иначе станция придет в намеченный район встречи либо раньше, либо позже планеты. У планеты сближения с сидерическим периодом обращения Т2 среднее суточное движение.
и за найденную по формуле (85) продолжительность полета станции Δt (выраженную в сутках) планета должна прийти в район встречи A, пройдя по своей орбите путь
Следовательно, в день t1 старта межпланетной станции разность гелиоцентрической долг
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 2630; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.012 с.) |





 +η, (16)
+η, (16)


 cos z = sin φ · sin δ + cos φ · cos δ · cos t, (28)
cos z = sin φ · sin δ + cos φ · cos δ · cos t, (28)
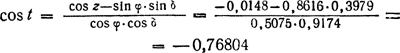
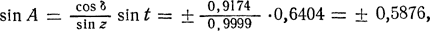







 (78)
(78) (79)
(79) (80)
(80) (81)
(81)
 (85)
(85) ,
,
 (87)
(87)




