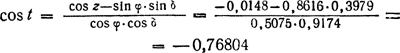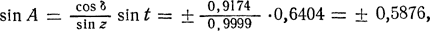Практическое определение географических и небесных экваториальных координат

В долгие зимние ночи астрономы измеряют зенитные расстояния одних и тех же звезд в обеих кульминациях и по формулам (4), (6), (9) независимо находят их склонение (δ) и географическую широту (φ) обсерватории. Зная φ, определяют склонение светил, у которых наблюдается только верхняя кульминация. При высокоточных измерениях учитывается рефракция, которая здесь не рассматривается, кроме случаев расположения светил вблизи горизонта.

В истинный полдень регулярно измеряют зенитное расстояние z Солнца и отмечают показание Sч звезд ных часов, затем по формуле (4) вычисляют его склонение δ , а по нему — прямое восхождение αsun, поскольку

sin α =tg δ -ctg ε, (24)

где ε = 23°27' — уже известное наклонение эклиптики.

Одновременно определяется и поправка звездных часов

us = S—Sч = α —Sч, (25)

так как в истинный полдень часовой угол Солнца t =0 и поэтому, согласно формуле (13), звездное время S = α .

Отмечая показания S'ч тех же часов в моменты верхней кульминации ярких звезд (они видны в телескопы и днем), находят их прямое восхождение

α=α + (S'ч—Sч) (26)

и по нему аналогичным образом определяют прямое восхождение остальных светил, которое также может быть найдено как

α=S'ч +us. (27)

По публикуемым в астрономических справочниках экваториальным координатам (α и δ) звезд определяют географические координаты мест земной поверхности.

Пример 1. В истинный полдень 22 мая 1975 г. зенитное расстояние Солнца в Пулкове было 39°33' S (над точкой юга), а звездные часы показывали 3ч57м41с. Вычислить для этого момента экваториальные координаты Солнца и поправку звездных часов. Географическая широта Пулкова φ = +59°46'.

Данные: z =39°33' S; Sч = 3ч57м41c; φ= + 59°46'.

Решение. Согласно формуле (4), склонение Солнца

δ =φ—z = 59°46'—39°33' = +20°13'. По формуле (24)

sinα = tgδ -ctgε = tg 20°13' - ctg 23°27' = +0,3683-2,3053=+0,8490,

откуда прямое восхождение Солнца α = 58°06',2, или, переведя в единицы времени, α = 3ч52м25c.

Так как в истинный полдень, согласно формуле (13), звездное время S = α =3ч52м25с, а звездные часы показывали Sч=3ч57м41c, то, по формуле (25), поправка часов

us=S—Sч=α —Sч = 3ч52м25с—3ч57м41с= —5м16с.

Пример 2. В момент верхней кульминации звезды α Дракона на зенитном расстоянии 9°17' к северу звездные часы показывали 7ч20м38с, причем их поправка к звездному гринвичскому времени равнялась +22м16с. Экваториальные координаты α Дракона: прямое восхождение 14ч03м02с и склонение + 64°37'. Определить географические координаты места наблюдения.

Данные: звезда, α = 14ч03м02с, δ=+64°37', zв = 9°17' N; звездные часы Sч = 7ч20м38с, us = 22м16с.

Решение. По формуле (6), географическая широта

φ = δ—zв = + 64°37'—9° 17'= + 55°20'.

Согласно формуле (13), звездное время в месте наблюдения

S =α=14ч03м02c, а звездное время в Гринвиче S0 = Sч+us=7ч20м38c+22м16c = 7ч42м54c.

Следовательно, по формуле (14), географическая долгота

λ = S—S0 = 14ч03м02с—7ч42м54с = 6ч20м08с,

или, переведя в угловые единицы, λ=95°02'.

Задача 70. Определить географическую широту места наблюдения и склонение звезды по измерениям ее зенитного расстояния z или высоты h в обеих кульминациях—верхней (в) и нижней (н):

а) zв=15°06'W, zн = 68°14' N;

б) zв=15°06' S, zн=68°14' N;

в) hв=+80°40' ю, zн=72°24' c;

г) hв=+78°08'ю, hн= + 17°40' ю.

Задача 71. В местности с географической широтой φ = = +49°34' звезда α Гидры проходит верхнюю кульминацию на высоте +32°00' над точкой юга, а звезда β малой медведицы — к северу от зенита на расстоянии в 24°48'. Чему равно склонение этих звезд?

Задача 72. Какое склонение имеют звезды, которые в верхней кульминации в Канберре (φ = —35°20') находятся на зенитном расстоянии 63°39' к северу от зенита и на высоте +58°42' над точкой юга?

Задача 73. В Душанбе звезда Капелла (α Возничего) проходит верхнюю кульминацию на высоте +82°35' при азимуте 180°, а звезда Альдебаран (α Тельца), склонение которой +16°25', — на зенитном расстоянии 22°08' к югу от зенита. Чему равно склонение Капеллы?

Задача 74. Вычислить склонение звезд δ Большой медведицы и Фомальгаута (α Южной Рыбы), если разность зенитных расстояний этих звезд и Альтаира (α Орла) в верхней кульминации в Ташкенте (φ=+41°18') составляет соответственно —48°35' и +38°38'. Альтаир кульминирует в Ташкенте на высоте +57°26' над точкой юга.

Задача 75. Какое склонение у звезд, кульминирующих на горизонте и в зените Тбилиси, географическая широта которого + 41°42'? Рефракцию в горизонте принять 35'.

Задача 76. Найти прямое восхождение звезд, в моменты верхней кульминации которых звездные часы показывали 18ч25м32с и 19ч50м40с, если при их показании 19ч20м16с звезда Альтаир (α Орла) с прямым восхождением 19ч48м21с пересекла небесный меридиан к югу от зенита.

Задача 77. В момент верхней кульминации Солнца его прямое восхождение было 23ч48м09с, а звездные часы показывали 23ч50м01с. За 46м48с до этого небесный меридиан пересекла звезда β Пегаса, а при показаниях тех же часов 0ч07м40с наступила верхняя кульминация звезды α Андромеды. Какое прямое восхождение у этих двух звезд?

Задача 78. 27 октября 1975 г. в Одессе Марс прокульминиро-вал через 15м50с по звездным часам после звезды Бе-тельгейзе (α Ориона) на высоте, превышающей высоту этой звезды в кульминации на 16°33', Прямое восхождение Бетельгейзе 5ч52м28с и склонение +7°24'. Какие экваториальные координаты были у Марса и вблизи какой точки эклиптики он находился?

Задача 79. 24 августа 1975 г. в Москве (φ = +55°45'), когда звездные часы показывали 1ч52м22с, Юпитер пересек небесный меридиан на зенитном расстоянии 47°38'. В 2ч23м31с по тем же часам прокульминировала звезда α Овна, прямое восхождение которой 2ч04м21с Чему были равны экваториальные координаты Юпитера?

Задача 80. В пункте с географической широтой +50°32' полуденная высота Солнца 1 мая и 11 августа равнялась + 54°38', а 21 ноября и 21 января +19°29'. Определить экваториальные координаты Солнца в эти дни.

Задача 81. В истинный полдень 4 июня 1975 г. Солнце прошло в Одессе (φ = +46°29') на высоте +65°54', а за 13м44с до этого звезда Альдебаран (α Тельца) пересекла небесный меридиан на зенитном расстоянии, превышающем полуденное зенитное расстояние Солнца на 5°58'. Определить экваториальные координаты Солнца и звезды.

Задача 82. 28 октября 1975 г. в 13ч06м41с по декретному времени в пункте с λ = 4ч37м11с (n=5) и φ=+41°18' зенитное расстояние Солнца было 54°18'. За 45м45с (по звездному времени) до этого в верхней кульминации находилась звезда Спика (α Девы), а через 51м39с после нее — звезда Арктур (α Волопаса) на высоте +68°01'ю. Определить экваториальные координаты Солнца и Арктура. Уравнение времени в этот день было — 16м08с.

Задача 83. Найти географическую широту местности, в которой звезды β Персея (δ = +40°46') и ε Большой Медведицы (δ = +56°14') в моменты верхней кульминации находятся на одинаковом зенитном расстоянии, но первая — к югу, а вторая — к северу от зенита.

Задача 84. В моменты верхней кульминации звезда α Гончих Псов со склонением +38°35' проходит в зените, звезда β Ориона — на 46°50' южнее, а звезда α Персея — на 11°06' севернее. На какой географической параллели проведены измерения и чему равно склонение указанных звезд?

Задача 85. В момент верхней кульминации Солнца средний хронометр показал 10ч28м30с, а при его показании 14ч48м52с был принят из Гринвича 12-часовой радиосигнал точного времени. Найти географическую долготу места наблюдения, если уравнение времени в этот день было +6м08с.

Задача 86. В момент верхней кульминации звезды ι Геркулеса на зенитном расстоянии в 2°14' к северу от зенита звездное гринвичское время было 23ч02м39с. Экваториальные координаты ι Геркулеса α=17ч38м03- и δ = +46°02', Определить географические координаты места наблюдения.

Задача 87. В момент показания звездного хронометра 18ч07м27с экспедиция приняла радиосигнал точного времени, переданный из Гринвича в 18ч0м0с по звездному гринвичскому времени. В момент верхней кульминации звезды γ Кассиопеи на зенитном расстоянии в 9°08' к югу от зенита показание того же хронометра было 19ч17м02с. Экваториальные координаты γ Кассиопеи α = 0ч53м40с и δ = +60°27'. Найти географические координаты экспедиции.

Задача 88. В истинный полдень показание среднего хронометра экспедиции было 11ч41м37с, а в момент приема 12-часового радиосигнала точного времени из Москвы тот же хронометр показал 19ч14м36с. Измеренное зенитное расстояние звезды α Лебедя (δ = +45°06') в верхней кульминации оказалось равным 3°26' к северу от зенита. Определить географические координаты экспедиции, если в день проведения наблюдений уравнение времени равнялось —5м 17с.

Задача 89. В истинный полдень штурман океанского лайнера измерил высоту Солнца, оказавшуюся равной +75°41' при азимуте 0°. В этот момент средний хронометр с поправкой — 16м,2 показывал 14ч12м,9 гринвичского времени. Склонение Солнца, указанное в морском астрономическом ежегоднике, было +23°19', а уравнение времени +2м55с. Какие географические координаты имел лайнер, где и в какие примерно дни года он в это время находился?

Ответы - Практическое определение географических и небесных экваториальных координат

 

Преобразование небесных координат и систем счета времени. Восход и заход светил

Связь между горизонтальными и экваториальными небесными координатами осуществляется через параллактический треугольник PZM (рис. 3), вершинами которого служат полюс мира Р, зенит Ζ и светило M, а сторонами — дуга ΡΖ небесного меридиана, дуга ΖΜ круга высоты светила и дуга РМ его круга склонения. Оче видно, что ΡΖ=90°—φ, ZM = z = 90°—h и PM=90°—δ, где φ — географическая широта места наблюдения, z — зенитное расстояние, h — высота и δ — склонение светила.

В параллактическом треугольнике угол при зените равен 180°—A, где A — азимут светила, а угол при полюсе мира — часовому углу t того же светила. Тогда горизонтальные координаты вычисляются по формулам

cos z = sin φ · sin δ + cos φ · cos δ · cos t, (28)

sin z · cos A = - sin δ · cos φ+cos δ · sin φ · cos t, (29)

sin z · sin A = cos δ · sin t, (30)

а экваториальные координаты — по формулам

sin δ = cos z · sin φ — sin z · cos φ · cos A, (31)

cos δ · cos t = cos z · cos φ+sin z · sin φ · cos A, (32)

cos δ · sin t=sin z · sin A, (30)

причем t = S — α, где α — прямое восхождение светила и S — звездное время.

 

Рис. 3. Параллактический треугольник

 

При расчетах необходимо по таблице 3 переводить интервалы звездного времени ΔS в интервалы среднего времени ΔT (или наоборот), а звездное время s0 — в среднюю гринвичскую полночь заданной даты заимствовать из астрономических календарей-ежегодников (в задачах этого раздела значения s0 приводятся).

Пусть некоторое явление в каком-то пункте земной поверхности произошло в момент Τ по принятому там времени. В зависимости от принятой системы счета времени по формулам (19), (20) или (21) находится среднее гринвичское время T0, представляющее собой интервал среднего времени ΔT, протекший с гринвичской полночи (ΔT=T0). Этот интервал по таблице 3 переводится в интервал звездного времени ΔS (т. е. ΔT→ΔS), и тогда в заданный момент T соответствующий среднему гринвичскому времени T0, звездное время в Гринвиче

S0=s0+ΔS, (33)

а в данном пункте

S = S0+λ, (14)

где λ — географическая долгота места,

Перевод интервалов звездного времени ΔS в интервалы среднего времени ΔΤ = Τ0 (т. е. ΔS→ΔT) осуществляется по таблице 3 вычитанием поправки.

Моменты времени и азимуты точек восхода и захода светил вычисляются по формулам (28), (29), (30) и (13), в которых принимается z=90°35' (с учетом рефракции ρ = 35').

Найденные значения часового угла и азимута в пределах от 180 до 360° соответствуют восходу светила, а в пределах от 0 до 180° — его заходу.

При вычислениях восхода и захода Солнца учитывается еще его угловой радиус r=16'. Найденные часовые углы t дают моменты по истинному солнечному времени (см. формулу (17), которые но формуле (16) переводятся в моменты среднего времени, а затем — в принятую систему счета.

Моменты восхода и захода всех светил вычисляются с точностью, не превышающей 1м.

Преобразование небесных координат и систем счета времени – Пример 1

В каком направлении был заранее установлен телескоп с фотокамерой для фотографирования солнечного затмения 29 апреля 1976 г., если в пункте с географическими координатами λ=2ч58м,0 и φ = +40°14' середина затмения наступила в 15ч29м,8 по времени, отличающемуся от московского на +1ч? В этот момент экваториальные координаты Солнца: прямое восхождение α=2ч27м,5 и склонение δ= + 14°35'. В среднюю гринвичскую полночь 29 апреля 1976 г. звездное время s0=14ч28м19c.

Данные: пункт наблюдения, λ = 2ч58м,0, φ = +40°14', T=15ч29м,8, Τ—Tм=1ч; s0 = 14ч28м19c = 14ч28м,3; Солнце, α=2ч27м,5, δ = +14°35'.

Решение. В середине затмения московское время Тм = Т—1ч=14ч29м,8, и поэтому среднее гринвичское время T0 = Tм—3ч = 11ч29м,8. С гринвичской полночи прошел интервал времени ΔТ = Т0 = 11ч29м,8, который переводим по таблице 3 в интервал звездного времени ΔS=11ч31м,7, и тогда в момент T0, по формуле (33), звездное время в Гринвиче

S0=s0+ΔS = 14ч28м,3 + 11ч31м,7 = 25ч60м = = 2ч0м,0

а в заданном пункте, по формуле (14), звездное время S = S0+λ=2ч0м,0 + 2ч58м,0 = 4ч58м,0

и, по формуле (13), часовой угол Солнца

t = S—α = 4ч58м, 0—2ч27м, 5 = 2ч30м, 5,

или, переводя по таблице 1, t = 37°37',5 ~ 37°38'. По таблицам тригонометрических функций находим:

sin φ = sin 40°14' = +0,6459,

cos φ = cos 40°14' = +0,7634;

sin δ = sin 14°35' = +0,2518,

cos δ = cos 14°35' = +0,9678;

sin t = sin 37°38' = +0,6106,

cos t = cos 37°38' = +0,7919.

По формуле (28) вычисляем

cos z = 0,6459 · 0,2518 + 0,7634 · 0,9678 · 0,7919 = = +0,7477

и по таблицам находим z = 41°36' и sin z = +0,6640. Для вычисления азимута используем формулу (30):

откуда получаем два значения: A = 62°52' и A = 180° — 62°52' = 117°08'. При δ<φ значения A и t не слишком резко отличаются друг от друга и поэтому A=62°52'.

Следовательно, телескоп был направлен в точку неба с горизонтальными координатами A=62°52' и z = 41°36' (или h = + 48°24').

Преобразование небесных координат и систем счета времени - Пример 2

Вычислить азимуты точек и моменты восхода и захода Солнца, а также продолжительность дня и ночи 21 июня 1975 г. в местности с географическими координатами λ=4ч28м,4 и φ = +59°30', находящейся в пятом часовом поясе, если в полдень этого дня склонение Солнца δ = +23°27', а уравнение времени η = + 1м35с.

Данные: Солнце, δ = +23°27'; η = +1м35с = +1м,6; место, λ=4ч28м,4, φ = 59°30', n = 5.

Решение. Учитывая среднюю рефракцию в горизонте ρ = 35' и угловой радиус солнечного диска r =16', находим, что в момент восхода и захода Солнца центр солнечного диска находится под горизонтом, на зенитном расстоянии

z = 90° + ρ + r = 90°51',

Тогда

sin z = +0,9999, cos z = -0,0148, sin δ = + 0,3979,

cos δ = +0,9174, sin φ = +0,8616, cos φ = +0,5075.

По формуле (28) находим:

и по таблицам

t = ± (180°—39°49',3) = ±140°10',7 и

sin t = ±0,6404.

По таблице 2 получим, что при восходе Солнца его часовой угол t1 = -140°10',7 = -9ч20м,7, а при заходе t2 = +140°10',7 = +9ч20м,7, т. е. по истинному солнечному времени, согласно формуле (17), Солнце восходит в

T 1 = 12ч + t1 = 12ч—9ч20м,7 = 2ч39м,3

и заходит в

T 2 =12ч + t2 = 12ч+9ч20м,7 = 21ч20м,7,

что, по формуле (16), соответствует моментам по сред нему времени

Tλ1 = T 1 + η = 2ч39м,3 + 1м,6=2ч41м и

Τλ2 = T 2 + η = 21ч20м,7+1м,6 = 21ч22м.

По формулам (19), (20) и (21) те же моменты по поясному времени: восход

Tn1 = Tλ1— λ+n = 2ч41м — 4ч28м + 5ч = 3ч13м

и заход Tn2 = Tλ2 — λ+n = 21ч22м — 4ч28м + 5ч = 21ч54м,

а по декретному времени:

восход Tд1=4ч13м и заход Tд2 = 22ч54м.

Продолжительность дня τ = Тд2—Тд1 = 22ч54м—4ч13м = 18ч41м.

В момент нижней кульминации высота Солнца

hн = δ— (90°—φ) = +23°27' - (90°—59°30') = -7°03', т. е. вместо обычной длится белая ночь.

Азимуты точек восхода и захода Солнца вычисляются по формуле (30):

что дает A = ±(180°—36°,0) = ±144°,0, так как азимуты и часовые углы Солнца находятся в одном квадранте. Следовательно, Солнце восходит в точке истинного горизонта с азимутом A1 = -144°,0 = 216°,0 и заходит в точке с азимутом A2 = +144°,0, расположенных в 36° по обе стороны от точки севера.

Задача 90. Через какие интервалы среднего времени чередуются одноименные и разноименные кульминации звезд?

Задача 91. Через сколько времени после верхней кульминации Денеба наступит верхняя кульминация звезды γ Ориона, а затем — снова верхняя кульминация Денеба? Прямое восхождение Денеба 20ч39м44с, а γ Ориона 5ч22м27с. Искомые интервалы выразить в системах звездного и среднего времени.

Задача 92. В 14ч15м10с по среднему времени звезда Сириус (α Большого Пса) с прямым восхождением 6ч42м57с находилась в нижней кульминации. В какие ближайшие моменты времени после этого звезда Гемма (α Северной Короны) будет находиться в верхней кульминации и когда ее часовой угол будет равен 3ч16м0с? Прямое восхождение Геммы 15ч32м34с.

Задача 93. В 4ч25м0с часовой угол звезды с прямым восхождением 2ч12м30с был равен —34°26',0. Найти прямое восхождение звезд, которые в 21ч50м0с будут находиться в верхней кульминации и в нижней кульминации, а также тех звезд, часовые углы которых станут равными — 1ч13м20с и 5ч42м50с.

Задача 94. Чему равно приближенное значение звездного времени в среднюю, поясную и декретную полночь Ижевска (λ = 3ч33м, n = 3) 8 февраля и 1 сентября?

Задача 95. Примерно в какие дни года звезды Сириус (α = 6ч43м) и Антарес (α = 16ч26м) находятся в верхней и нижней кульминации в среднюю полночь?

Задача 96. Определить звездное время в Гринвиче в 7ч28м16с 9 января (s0 = 7ч11м39c)* и в 20ч53м47с 25 июля (s0 = 20ч08м20с).

* Здесь и далее в скобках после дат указано звездное время в среднюю гринвичскую полночь.

Задача 97. Найти звездное время в средний, поясной и декретный полдень, а также в среднюю, поясную и декретную полночь в Москве (λ = 2ч30м17с, n=2) 15 января (s0=7ч35м18c).*

* Здесь и далее в скобках после дат указано звездное время в среднюю гринвичскую полночь.

Задача 98. Решить предыдущую задачу для Красноярска (λ = 6ч11м26с, n = 6) и Охотска (λ = 9ч33м10с, n=10) в день 8 августа (s0=21ч03м32c).

Задача 99. Вычислить часовые углы звезды Деиеба (α Лебедя) (α = 20ч39м44с) в Гринвиче в 19ч42м10с 16 июня (S0=17ч34м34с) и 16 декабря (S0=5ч36м04c).

Задача 100. Вычислить часовые углы звезд α Андромеды (α = 0ч05м48с) и β Льва (α= 11ч46м31с) в 20ч32м50с 3 августа (s0=20ч43M40c) и 5 декабря (s0=4ч52M42c) во Владивостоке (λ=8ч47м31с, n = 9).

Задача 101. Найти часовые углы звезд Бетельгейзе (α = 5ч52м28с) и Спики (α =13ч22м33с) в 1ч52м36с 25 июня (s0=18ч06м07c) и 7 ноября (s0=2ч58м22c) в Ташкенте (λ=4ч37м11с, n=5).

Задача 102. В какие моменты времени в Гринвиче находятся в верхней кульминации звезда Поллукс (α = 7ч42м16с), а в нижней кульминации звезда Арктур (α =14ч13м23с) 10 февраля (s0=9ч17м48c) и 9 мая (s0=15ч04м45c)?

Задача 103. Найти моменты верхней и нижней кульминации 22 марта (s0 = 11ч55м31c) и 22 июня (s0 = 17ч58м14c) звезд Капеллы (α = 5ч13м00с) и Беги (α = 18ч35м15с) на географическом меридиане λ = 3ч10м0с (n = 3). Моменты указать по звездному, среднему, поясному и декретному времени.

Задача 104. В какие моменты времени 5 февраля (s0 = 8ч58м06с) и 15 августа (s0 = 21ч31м08c) часовые углы звезд Сириуса (α = 6ч42м57с) и Альтаира (α = 19ч48м21с) в Самарканде (λ = 4ч27м53с, n = 4) равны 3ч28м47с?

Задача 105. В какие моменты времени 10 декабря (s0 =5ч12м24с) часовые углы звезд Альдебарана (α = 4ч33м03с) и β Лебедя (α = 19ч28м42с) в Тбилиси (λ = 2ч59м11с, n = 3) и в Охотске (λ = 9ч33м10с, n=10) соответственно равны +67°48' и —24°32'?

Задача 106. На каких географических меридианах звезды α Близнецов и γ Большой Медведицы находятся в верхней кульминации 20 сентября (s0=23ч53м04c) в 8ч40м26с по времени Иркутска (n=7)? Прямое восхождение этих звезд соответственно равно 7ч31м25с и 11ч51м13с.

Задача 107. Определить горизонтальные координаты звезд ε Большой Медведицы (а = 12ч51м50с, δ = +56°14') и Антареса (α = 16ч26м20с, δ = -26°19') в 14ч10м0с по звездному времени в Евпатории (φ = +45°12').

Задача 108. Чему равны горизонтальные координаты звезд Геммы (α = 15ч32м34с, δ = +26°53') и Спики (α = 13ч22м33с, δ = —10°54') 15 апреля (s0 = 13ч30м08c) и 20 августа (s0 = 21ч50м50c) в 21ч30м по декретному времени в пункте с географическими координатами λ = 6ч50м0с (n = 7) и φ = +71°58'?

Задача 109. В какие точки неба, определяемые горизонтальными координатами, необходимо направить телескоп, установленный в пункте с географическими координатами λ = 2ч59м,2 (n = 3) и φ = +41°42', чтобы 4 мая 1975 г. (s0=14ч45м02с) в 22ч40м по поясному времени увидеть

Уран (α = 13ч52м,1, δ = —10°55') и Нептун (α = 16ч39м,3, δ = -20с32')?

Задача 110. В какие моменты времени восходит, кульминирует и заходит и сколько времени находится над горизонтом точка летнего солнцестояния 22 марта (s0 = 11ч55м31с) и 22 июня (s0=17ч58м14c) на центральном меридиане второго часового пояса в местах с географической широтой φ = +37°45' и φ = +68°20'? Моменты выразить по звездному и декретному времени.

Задача 111. Вычислить азимуты и моменты восхода, верхней кульминации, захода и нижней кульминации звезд Кастора (α = 7ч31м25с, δ = +32°00') и Антареса (α = 16ч26м20с, δ = —26°19') 15 апреля (s0=13ч30м08c) и 15 октября (s0=1ч31м37c) в местах земной поверхности с географическими координатами λ =3ч53м33с (n = 4), φ = +37°45' и λ = 2ч12м15с (n = 2), φ = +68°59'.

Задача 112. Вычислить азимуты и моменты восхода, верхней кульминации и захода Солнца, его полуденную и полуночную высоту, а также продолжительность дня в даты весеннего равноденствия и обоих солнцестояний в пунктах с географическими координатами λ = 2ч36м,3 (n=2), φ = +59°57', и λ = 5ч53м,9 (n = 6), φ = +69°18'. В последовательные даты уравнение времени соответственно равно +7м23с, +1м35с и —2м08с.

Задача 113. В какие моменты времени 30 июля (s0 = 20ч28м03с) в пункте с λ = 2ч58м0с (n=3) и φ = +40°14' нижеперечисленные звезды имеют горизонтальные координаты A и z:

Звезда	α	δ	А	z
Сириус (α Большого Пса) Регул (α Льва) Капелла (α Возничего)	6ч42м57с 10ч05м43с 5ч13м0с	—16°39' + 12°13 + 45°58	— 40°10' + 65°05 + 152°55	67°08' 46°28 86°25

Задача 114. В пункте с географическими координатами λ= 4ч37м11c (n = 5) и φ = + 41°18' 5 августа 1975 г. (s0= 20ч51м42с) были измерены горизонтальные координаты двух звезд: в 21ч10м у первой звезды A = —8°33' и z =49°51', а в 22ч50м у второй звезды A = 46°07' и z = 38°24'. Вычислить экваториальные координаты этих звезд.

Ответы - Преобразование небесных координат и систем счета времени