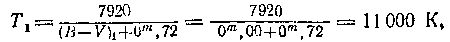Физическая природа Солнца и звезд

Светимость звезд вычисляется по их абсолютной звездной величине М, которая связана с видимой звездной величиной m соотношениями

M = m + 5 + 51gπ (116)

и

M = m + 5 — 51gr, (117)

где π — годичный параллакс звезды, выраженный в секундах дуги (") и r — расстояние звезды в парсеках (пс). Найденная по формулам (116) и (117) абсолютная звездная величина Μ принадлежит к тому же виду, что и видимая звездная величина m, т. е. может быть визуальной Μ_v, фотографической M_pg, фотоэлектрической (M_v, M_в или М_v) и т. д. В частности, абсолютная болометрическая звездная величина, характеризующая полное излучение,

M_b = M_v + b (118)

и может быть также вычислена по видимой болометри ческой звездной величине

m_b = m_v + b, (119)

где b — болометрическая поправка, зависящая от спектрального класса и класса светимости звезды.

Светимость L звезд выражается в светимости Солнца, принятой за единицу (L = 1), и тогда

lg L = 0,4(M - M), (120)

где M — абсолютная звездная величина Солнца: визуальная M _v = +4^m,79; фотографическая M _pg — = +5m,36; фотоэлектрическая желтая Μ ν = +4^m77; фотоэлектрическая синяя M _B = 5^m,40; болометрическая M _b = +4^m,73. Эти звездные величины необходимо использовать при решении задач данного раздела.

Вычисленная по формуле (120) светимость звезды соответствует виду абсолютных звездных величин звезды и Солнца.

Закон Стефана—Больцмана

применим для определения эффективной температуры Т_е только тех звезд, у которых известны угловые диаметры. Если Ε— количество энергии, падающей от звезды или Солнца по нормали на площадку в 1 см² границы земной атмосферы за 1c, то при угловом диаметре Δ, выраженном в секундах дуги ("), температура

(121)

где σ= 1,354·10^-12 кал/(см²·с·град⁴) = 5,70·10^-5 эрг/(см2·с·град⁴) и выбирается в зависимости от единиц измерения количества энергии E, которое находится из формулы (111) по разности болометрических звездных величин звезды и Солнца путем сравнения с солнечной постоянной Ε ~ 2 кал/(см2·мин).

Цветовая температура Солнца и звезд, в спектрах которых известно распределение энергии, может быть найдена по закону Вина

Τ = K/λ_m, (122)

где λ_m — длина волны, соответствующая максимуму энергии, а К — постоянная, зависящая от единиц измерения λ. При измерении λ в см К=0,2898 см·град, а при измерении λ в ангстремах (Å) K=2898· 10⁴ Å·град.

С достаточной степенью точности цветовая температуpa звезд вычисляется по их показателям цвета С и (B-V)

(123)

и

(124)

Массы Μ звезд обычно выражаются в массах Солнца (Μ = 1) и надежно определяются только для физических двойных звезд (с известным параллаксом π) по третьему обобщенному закону Кеплера: сумма масс компонентов двойной звезды

Μ₁ + М₂ = a³ / P², (125)

где Ρ — период обращения звезды-спутника вокруг главной звезды (или обеих звезд вокруг общего центра масс), выраженный в годах, и а — большая полуось орбиты звезды-спутника в астрономических единицах (а. е.).

Величина а в а. е. вычисляется по угловому значению большой полуоси а" и параллаксу π, полученным из наблюдений в секундах дуги:

а = а"/π (126)

Если известно отношение расстояний а₁ и а₂ компонентов двойной звезды от их общего центра масс, то равенство

M₁/M₂ = а₂/а₁ (127)

позволяет вычислить массу каждого компонента в отдельности.

Линейные радиусы R звезд всегда выражаются в радиусах Солнца (R = 1) и для звезд с известными угловыми диаметрами Δ (в секундах дуги)

(128)

причем

lgΔ = 5,444 — 0,2 m_b —2 lg T (129)

Линейные радиусы звезд вычисляются также по формулам

lgR = 8,473—0,20M_b—2 lgT (130)

lgR = 0,82C—0,20M_v + 0,51 (131)

и lgR = 0,72(B—V) — 0,20 M_v + 0,51, (132)

в которых Т — температура звезды (строго говоря, эффективная, но если она не известна, то цветовая).

Так как объемы звезд всегда выражаются в объемах Солнца, то они пропорциональны R³, и поэтому средняя плотность звездного вещества (средняя плотность звезды)

(133)

где ρ —средняя плотность солнечного вещества.

При ρ = 1 средняя плотность звезды получается в плотностях солнечного вещества; если же нужно вычислить ρ в г/см3, следует принять ρ =1,41 г/см³.

Мощность излучения звезды или Солнца

(134)

а ежесекундная потеря массы через излучение определяется по формуле Эйнштейна

(135)

где с = 3 · 10¹⁰ см/с — скорость света, ΔΜ — выражается в граммах в секунду и ε ₀— в эргах в секунду.

Пример 1. Определить эффективную температуру и радиус звезды Веги (а Лиры), если ее угловой диаметр равен 0",0035, годичный параллакс 0",123 и болометрический блеск — 0^m,54. Болометрическая звездная величина Солнца равна —26^m,84, а солнечная постоянная близка к 2 кал/(см²·мин).

Данные: Вега, Δ=3",5·10^-3, π = 0",123, m_b = —0^m,54;

Солнце, m _b = — 26m,84, E = 2 кал/(см²·мин) = 1/30 кал/(см²·с); постоянная σ= 1,354 x 10^-12 кал/(см²·с·град⁴).

Решение. Падающее нормально на единицу площади земной поверхности излучение звезды, аналогичное солнечной постоянной, вычисляется по формуле (111):

lg E/E=0,4 (m_b - m_b) = 0,4 (—26^m,84 + 0^m,54) = —10,520 = —11 + 0,480,

откуда E/E = 3,02 · 10^-11,

или Ε = 3,02· 10^-11· 1/30 = 1,007·10^-12 кал/(см2 · с).

Согласно (121), эффективная температура звезды

По формуле (128), радиус Веги

Пример 2. Найти физические характеристики звезды Сириуса (а Большого Пса) и его спутника по следующим данным наблюдений: видимая желтая звездная величина Сириуса равна —1^m,46, его основной показатель цвета 0^m,00, a у звезды-спутника соответственно +8^m,50 и +0^m,15; параллакс звезды равен 0",375; спутник обращается вокруг Сириуса с периодом 50 лет по орбите с угловым значением большой полуоси 7",60, причем отношение расстояний обеих звезд до общего центра масс составляет 2,3:1. Абсолютную звездную величину Солнца в желтых лучах принять равной +4^m,77.

Данные: Сириус, V₁ = — 1^m,46, (В—V)₁ = 0^m,00;

спутник, V₂= +8^m,50, (B-V)₂ = +0^m,15, P = 50 лет, a"=7",60; а₂/а₁ = 2,3:1; п=0",375.

Солнце, M _v = +4^m,77.

Решение. Согласно формулам (116) и (120), абсолютная звездная величина Сириуса

M_v1 = V₁ + 5 + 5 lgп = -1^m,46 + 5 + 5 lg 0,375 = +1^m,41, а логарифм его светимости

откуда светимость L₁ = 22.

По формуле (124), температура Сириуса

по формуле (132)

и тогда радиус Сириуса R₁ = 1,7, а его объем R₁³ =1,7³ = 4,91 (объема Солнца).

Те же формулы дают для спутника Сириуса: M_v2 = +11^m,37; L₂ = 2,3·10^-3; T₂ = 9100°; R₂ = 0,022; R₂³ = 10,6·10^-6.

По формуле (126), большая полуось орбиты спутника

по (125) сумма масс обеих звезд

и, по (127), отношение масс

откуда при совместном решении уравнений (125) и (127) находится масса Сириуса Μ₁ = 2,3 и масса его спутника М₂ = 1,0

Средняя плотность звезд вычисляется по формуле (133): у Сириуса

а у его спутника

По найденным характеристикам — радиусу, светимости и плотности — видно, что Сириус принадлежит к звездам главной последовательности, а его спутник является белым карликом.

Задача 284. Вычислить визуальную светимость звезд, визуальный блеск и годичный параллакс которых указаны в скобках: α Орла (0m,89 и 0",198), α Малой Медведицы (2m, 14 и 0",005) и ε Индейца (4m,73 и 0",285).

Задача 285. Найти фотографическую светимость звезд, для которых визуальный блеск, обычный показатель цвета и расстояние от Солнца указаны в скобках: β Близнецов (lm,21, +1m,25 и 10,75 пс); η Льва (3m,58, +0m,00 и 500 пс); звезда Каптейна (8m,85, + 1m,30 и 3,98 пс). Звездная величина Солнца указана в задаче 275.

Задача 286. Во сколько раз визуальная светимость звезд предыдущей задачи превышает их фотографическую светимость?

Задача 287. Визуальный блеск Капеллы (а Возничего) равен 0m,21, а ее спутника 10m,0. Показатели цвета этих звезд равны соответственно +0m,82 и +1m,63. Определить, во сколько раз визуальная и фотографическая светимость Капеллы больше соответствующей светимости ее спутника.

Задача 288. Абсолютная визуальная звездная величина звезды β Большого Пса равна—2m,28. Найти визуальную и фотографическую светимость двух звезд, одна из которых (с показателем цвета +0m,29) в 120 раз абсолютно ярче, а другая (с показателем цвета +0m,90) в 120 раз абсолютно слабее звезды β Большого Пса.

Задача 289. Если бы Солнце, Ригель (β Ориона), Толиман (а Центавра) и его спутник Проксима (Ближайшая) находились на одинаковом расстоянии от Земли, то какое количество света в сравнении с солнечным получала бы она от этих звезд? Визуальный блеск Ригеля 0m,34, его параллакс 0",003, те же величины у Толимана 0m, 12 и 0",751, а у Проксимы 10m,68 и 0",762. Звездная величина Солнца указана в задаче 275.

Задача 290. Найти расстояния от Солнца и параллаксы трех звезд Большой Медведицы по их блеску в желтых лучах и абсолютной звездной величине в синих лучах:

1) а, V = 1m,79, (В—V) = + lm,07 и Mв = +0m,32;

2) δ, V = 3m,31, (Β—V) = +0m,08 и Mв = + 1m,97;

3) η, V = 1m,86, (В—V) = —0m,19 и Мв = — 5m,32.

Задача 291. На каком расстоянии от Солнца находится звезда Спика (а Девы) и чему равен ее параллакс, если ее светимость в желтых лучах равна 720, основной показатель цвета равен —0m,23, а блеск в синих лучах 0m,74?

Задача 292. Абсолютная синяя (в В-лучах) звездная величина звезды Капеллы (а Возничего) +0m,20, a звезды Проциона (а Малого Пса) + 3m,09. Во сколько раз эти звезды в синих лучах абсолютно ярче или слабее звезды Регула (а Льва), абсолютная желтая (в V лучах) звездная величина которой равна —0m,69, а основной показатель цвета —0m,11?

Задача 293. Как выглядит Солнце с расстояния звезды Толимана (а Центавра), параллакс которой 0",751?

Задача 294. Каков визуальный и фотографический блеск Солнца с расстояний звезд Регула (а Льва), Антареса (а Скорпиона) и Бетельгейзе (а Ориона), параллаксы которых соответственно равны 0",039, 0",019 и 0",005?

Задача 295. На сколько болометрические поправки отличаются от основных показателей цвета при болометрической светимости звезды, превышающей в 20, 10 и 2 раза ее желтую светимость, которая, в свою очередь, больше синей светимости звезды соответственно в 5, 2 и 0,8 раза?

Задача 296. Максимум энергии в спектре Спики (а Девы) приходится на электромагнитную волну длиной 1450 Å, в спектре Капеллы (а Возничего) —на 4830 Å и в спектре Поллукса (β Близнецов)—на 6580 Å. Определить цветовую температуру этих звезд.

Задача 297. Солнечная постоянная периодически колеблется в пределах от 1,93 до 2,00 кал/(cм²·мин) На сколько при этом изменяется эффективная температура Солнца, видимый диаметр которого близок к 32"? Постоянная Стефана σ= 1,354 10^-12 кал/(см²·с·град⁴).

Задача 298. По результату предыдущей задачи найти приближенное значение длины волны, соответствующей максимуму энергии в солнечном спектре.

Задача 299. Определить эффективную температуру звезд по измеренным их угловым диаметрам и доходящему от них до Земли излучению, указанным в скобках:

α Льва (0",0014 и 3,23· 10^-11 кал/(см²·мин));

α Орла (0",0030 и 2,13· 10^-11 кал/(см²·мин));

α Ориона (0",046 и 7,70·10^-11 кал/(см²·мин)).

Задача 300. Видимая болометрическая звездная величина звезды α Эридана равна —1m,00 и угловой диаметр 0",0019, у звезды α Журавля аналогичные параметры +1m,00 и 0",0010, а у звезды α Тельца +0m,06 и 0",0180. Вычислить температуру этих звезд, приняв видимую болометрическую звездную величину Солнца равной —26m,84 и солнечную постоянную близкой к 2 кал/(см2 мин).

Задача 301. Определить температуру звезд, визуальный и фотографический блеск которых указан в скобках: γ Ориона (1m,70 и 1m,41); ε Геркулеса (3m,92 и 3m,92); α Персея (1m,90 и 2m,46); β Андромеды (2m,37 и 3m,94).

Задача 302. Вычислить температуру звезд по фотоэлектрической желтой и синей звездным величинам, указанным в скобках: ε Большого Пса (1m,50 и 1m,29); β Ориона (0m,13 и 0m,10); α Киля (—0m,75 и — 0m,60); α Водолея (2m,87 и 3m,71); α Волопаса (—0m,05 и 1m,18); α Кита (2m,53 и 4m,17).

Задача 303. По результатам двух предыдущих задач найти длину волны, соответствующую максимуму энергии в спектрах тех же звезд.

Задача 304. У звезды Беги (а Лиры) параллакс 0",123 и угловой диаметр 0",0035, у Альтаира (а Орла) аналогичные параметры 0",198 и 0",0030, у Ригеля (β Ориона) — 0",003 и 0",0027 и у Альдебарана (а Тельца) — 0",048 и 0",0200. Найти радиусы и объемы этих звезд.

Задача 305. Блеск Денеба (а Лебедя) в синих лучах 1m,34, его основной показатель цвета +0m,09 и параллакс 0",004; те же параметры у звезды ε Близнецов равны 4m,38, +1m,40 и 0",009, а у звезды γ Эридана 4m,54, + 1m,60 и 0",003. Найти радиусы и объемы этих звезд.

Задача 306. Сравнить диаметры звезды δ Змееносца и звезды Барнарда, температура которых одинакова, если у первой звезды видимая болометрическая звездная величина равна 1m,03 и параллакс 0",029, а у второй те же параметры 8m,1 и 0",545.

Задача 307. Вычислить линейные радиусы звезд, температура и абсолютная болометрическая звездная величина которых известны: у α Кита 3200° и —6m,75, у β Льва 9100° и +1m,18, а у ε Индейца 4000° и +6m,42.

Задача 308. Чему равны угловые и линейные диаметры звезд, видимая болометрическая звездная величина, температура и параллакс которых указаны в скобках: η Большой Медведицы (—0m,41, 15500° и 0",004), ε Большой Медведицы (+ lm,09, 10 000° и 0",008) и β Дракона (+ 2m,36, 5200° и 0",009)?

Задача 309. Если у двух звезд примерно одинаковой температуры радиусы различаются в 20, 100 и 500 раз, то во сколько раз различается их болометрическая светимость?

Задача 310. Во сколько раз радиус звезды α Водолея (спектральный подкласс G2Ib) превышает радиус Солнца (спектральный подкласс G2V), если ее видимая визуальная звездная величина 3m,19, болометрическая поправка —0m,42 и параллакс 0",003, температура обоих светил примерно одинакова, а абсолютная болометрическая звездная величина Солнца равна +4m,73?

Задача 311. Вычислить болометрическую поправку для звезд спектрального подкласса G2V, к которому принадлежит Солнце, если угловой диаметр Солнца 32', его видимая визуальная звездная величина равна —26m,78 и эффективная температура 5800°.

Задача 312. Найти приближенное значение болометрической поправки для звезд спектрального подкласса В0Iа, к которому принадлежит звезда ε Ориона, если ее угловой диаметр 0",0007, видимая. визуальная звездная величина 1m,75 и максимум энергии в ее спектре приходится на длину волны 1094 Å.

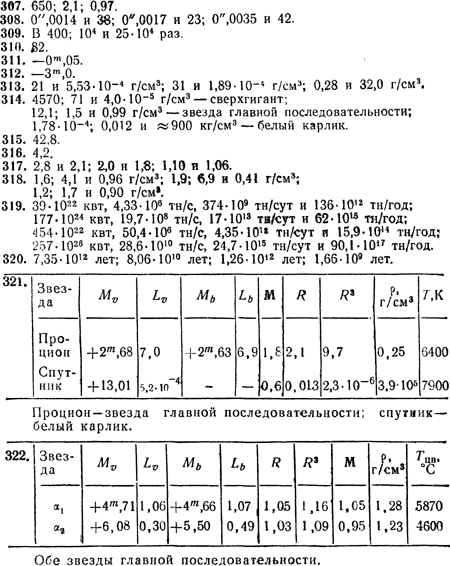
Задача 313. Вычислить радиус и среднюю плотность звезд, указанных в задаче 285, если масса звезды β Близнецов примерно 3,7, масса η Льва близка к 4,0, а масса звезды Каптейна 0,5.

Задача 314. Визуальный блеск Полярной звезды 2m,14, ее обычный показатель цвета +0m,57, параллакс 0",005 и масса равна 10. Те же параметры у звезды Фомальгаута (а Южной Рыбы) 1m,29, +0m,11, 0",144 и 2,5, а у звезды ван-Маанена 12m,3, + 0m,50, 0",236 и 1,1. Определить светимость, радиус и среднюю плотность каждой звезды и указать ее положение на диаграмме Герцшпрунга — Рессела.

Задача 315. Найти сумму масс компонентов двойной звезды ε Гидры, параллакс которой 0",010, период обращения спутника 15 лет и угловые размеры большой полуоси его орбиты 0",21.

Задача 316. Найти сумму масс компонентов двойной звезды α Большой Медведицы, параллакс которой 0",031, период обращения спутника 44,7 года и угловые размеры большой полуоси его орбиты 0",63.

Задача 317. Вычислить массы компонентов двойных звезд по следующим данным:

Звезда	Угловые размеры большой полуоси орбиты	Годичный параллакс	Период обращения	Отношение расстояний звезд от общего центра масс
α Возничего а Близнецов ξ Большой Медведицы	0",054 6", 29 2", 51	0",073 0",072 0",127	105 дней 420 лет 59,8 года	11:14 8:7 49:51

Задача 318. Для главных звезд предыдущей задачи вычислить радиус, объем и среднюю плотность. Видимая желтая звездная величина и основной показатель цвета этих звезд: α Возничего 0m,08 и +0m,80, α Близнецов 2m,00 и +0m,04 и ξ Большой Медведицы 3m,79 и +0m,59.

Задача 319. Для Солнца и звезд, указанных в задаче 299, найти мощность излучения и потерю массы за секунду, сутки и год. Параллаксы этих звезд следующие: α Льва 0",039, α Орла 0",198 и α Ориона 0",005.

Задача 320. По результатам предыдущей задачи вычислить продолжительность наблюдаемой интенсивности излучения Солнца и тех же звезд, полагая ее возможной до потери половины своей современной массы, которая (в массах Солнца) у α Льва равна 5,0, у α Орла 2,0 и у α Ориона 15. Массу Солнца принять равной 2·10³³ г.

Задача 321. Определить физические характеристики компонентов двойной звезды Процйоиа (а Малого Пса) и указать их положение на диаграмме Герцшпрунга—Рессела, если из наблюдений известны: визуальный блеск Проциона 0m,48, его обычный показатель цвета +0m,40, видимая болометрическая звездная величина 0m,43, угловой диаметр 0",0057 и параллакс 0",288; визуальный блеск спутника Проциона 10m,81, его обычный показатель цвета +0m,26, период обращения вокруг главной звезды — 40,6 года по орбите с видимой большой полуосью 4",55; отношение расстояний обеих звезд от их общего центра масс равно 19:7.

Задача 322. Решить предыдущую задачу для двойной звезды α Центавра. У главной звезды фотоэлектрическая желтая звездная величина равна 0m,33, основной показатель цвета +0m,63, видимая болометрическая звездная величина 0m,28; у спутника аналогичные величины суть 1m,70, + 1m,00 и 1m,12, период обращения 80,1 года на видимом среднем расстоянии 17",6; параллакс звезды 0",751 и отношение расстояний компонентов от их общего центра масс равно 10:9.

Ответы - Физическая природа Солнца и звезд

Кратные и переменные звезды

Блеск Ε кратной звезды равен сумме блеска Ε_i всех ее компонентов

E = E₁ + E₂ + E₃ +... = ΣE_ί, (136)

и поэтому ее видимая т и абсолютная Μ звездная величина всегда меньше соответствующей звездной величины m_i и M_i любого компонента. Положив в формуле Погсона (111)

lg (E/E₀) = 0,4 (m₀—m)

Е₀ = 1 и m₀ = 0, получим:

lg E = - 0,4 m. (137)

Определив по формуле (137) блеск E_i каждого компонента, находят по формуле (136) суммарный блеск Ε кратной звезды и снова по формуле (137) вычисляют m = —2,5 lg E.

Если заданы отношения блеска компонентов

E₁/E₂ = k,

E₃/E₁ = n

и т. д,, то блеск всех компонентов выражают через блеск одного из них, например E₂ = E₁/k, Ε₃ = n Ε₁ и т. д., и затем по формуле (136) находят Е.

Средняя орбитальная скорость ν компонентов затменной переменной звезды может быть найдена по периодическому наибольшему смещению Δλ линий (с длиной волны λ) от их среднего положения в ее спектре, так как в данном случае можно принять

v = v_r = c (Δλ/λ) (138)

где v_r — лучевая скорость и с = 3·10⁵ км/с — скорость света.

По найденным значениям v компонентов и периоду переменности Ρ звезды вычисляют большие полуоси a₁ и a₂ их абсолютных орбит:

a₁ = (v₁/2п) P и а₂ = (v₂/2п) P (139)

затем — большую полуось относительной орбиты

а = а₁ + а₂ (140)

и, наконец, по формулам (125) и (127)—массы компонентов.

Формула (138) позволяет также вычислить скорость расширения газовых оболочек, сброшенных новыми и сверхновыми звездами.

Пример 1. Вычислить видимую визуальную звездную величину компонентов тройной звезды, если ее визуальный блеск равен 3^m,70, второй компонент ярче третьего в 2,8 раза, а первый ярче третьего на 3^m,32.

Данные: m = 3^m,70; E₂/E₃ = 2,8; m₁ = m₃—3^m,32.

Решение. По формуле (137) находим

lgE = — 0,4m = - 0,4·3^m,70 = - 1,480 = 2,520

и E = 0,03311.

Чтобы воспользоваться формулой (136), необходимо найти отношение E₁/E₃; по (111),

lg (E₁/E₃) = 0,4 (m₃—m₁)= 0,4·3^m,32= 1,328

откуда E₁ = 21,3 E₃

Согласно (136),

E = E₁ + E₂ + E_з = 21,3 E₃ + 2,8 E₃ + E₃ = 25,1 E₃

и тогда

E₃ = E / 25,1 = 0,03311 / 25,1 = 0,001319 = 0,00132

E₂ = 2,8 E₃ = 2,8·0,001319 = 0,003693 = 0,00369

и E₁ = 21,3 E₃ = 21,3·0,001319 = 0,028094 = 0,02809.

По формуле (137)

m₁ = — 2,5 lg E₁= — 2,5·lg 0,02809 = — 2,5 ·2,449 = 3^m,88,

m₂ = — 2,5 lg E₂ = — 2,5·lg 0,00369 = — 2,5·3,567 = 6^m,08,

m₃ = —2,5 lg E₃ = — 2,5·lg 0,00132 = — 2,5·3,121 = 7^m,20.

Пример 2. В спектре затменной переменной звезды, блеск которой меняется за 3,953 сут, линии относительно их среднего положения периодически смещаются в противоположные стороны до значений в 1,9· 10^-4 и 2,9· 10^-4 от нормальной длины волны. Вычислить массы компонентов этой звезды.

Данные: (Δλ/λ)₁ = 1,9·10^-4; (Δλ/λ)₂ = 2,9·10^-4; Ρ = 3^д,953.

Решение. По формуле (138), средняя орбитальная скорость первого компонента

v₁ = v_r1 = c (Δλ/λ)₁ = 3·10⁵·1,9·10^-4; v₁ = 57 км/с,

Орбитальная скорость второго компонента

v₂ = v_r2 = с (Δλ/λ)₂ = 3·10⁵·2,9·10^-4;

v₂ = 87 км/с.

Чтобы вычислить значения больших полуосей орбит компонентов, необходимо период обращения Р, равный периоду переменности, выразить в секундах. Так как 1^д = 86400^с, то Ρ = 3,953·86400^c. Тогда, согласно (139), у первого компонента большая полуось орбиты

a₁ = 3,10·10⁶ км,

а у второго а₂ = (v₂/2п) P = (v₂/v₁) a₁, = (87/57)·3,10·10⁶;

a₂=4,73·10⁶ км,

и, по (140), большая полуось относительной орбиты

a = a₁ + a₂ = 7,83·10⁶; а = 7,83·10⁶ км.

Для вычисления суммы масс компонентов по формуле (125) следует выразить a в а. е. (1 а. е.= 149,6·10⁶км) и Р — в годах (1 год=365^д,3).

или М₁ + М₂ = 1,22 ~ 1,2.

Отношение масс, по формуле (127),

и тогда Μ₁ ~ 0,7 и М₂ ~ 0,5 (в массах Солнца).

Задача 323. Определить визуальный блеск двойной звезды α Рыб, блеск компонентов которой 4m,3 и 5m,2.

Задача 324. Вычислить блеск четырехкратной звезды ε Лиры по блеску ее компонентов, равному 5m,12; 6m,03; 5m,11 и 5m,38.

Задача 325. Визуальный блеск двойной звезды γ Овна 4m,02, а разность звездных величин ее компонентов составляет 0m,08. Найти видимую звездную величину каждого компонента этой звезды.

Задача 326. Какой блеск тройной звезды, если первый ее компонент ярче второго в 3,6 раза, третий — слабее второго в 4,2 раза и имеет блеск 4m,36?

Задача 327. Найти видимую звездную величину двойной звезды, если один из компонентов имеет блеск 3m,46, а второй на 1m,68 ярче первого компонента.

Задача 328. Вычислить звездную величину компонентов тройной звезды β Единорога с визуальным блеском 4m,07, если второй компонент слабее первого в 1,64 раза и ярче третьего на 1m,57.

Задача 329. Найти визуальную светимость компонентов и общую светимость двойной звезды α Близнецов, если ее компоненты имеют визуальный блеск 1m,99 и 2m,85, а параллакс равен 0",072.

Задача 330. Вычислить визуальную светимость второго компонента двойной звезды γ Девы, если визуальный блеск этой звезды равен 2m,91, блеск первого компонента 3m,62, а параллакс 0",101.

Задача 331. Определить визуальную светимость компонентов двойной звезды Мицара (ζ Большой Медведицы), если ее блеск равен 2m,17, параллакс 0",037, а первый компонент ярче второго в 4,37 раза.

Задача 332. Найти фотографическую светимость двойной звезды η Кассиопеи, визуальный блеск компонентов которой 3m,50 и 7m,19, их обычные показатели цвета +0m,571 и +0m,63, а расстояние 5,49 пс.

Задача 333. Вычислить массы компонентов затменных переменных звезд по следующим данным:

Звезда	Лучевая скорость компонентов	Период переменности
β Персея U Змееносца WW Возничего U Цефея	44 км/с и 220 км/с 180 км/с и 205 км/с 117 км/с и 122 км/с 120 км/с и 200 км/с	2^д,867 1^д,677 2^д,525 2^д,493

Задача 334. Во сколько раз меняется визуальный блеск переменных звезд β Персея и χ Лебедя, если у первой звезды он колеблется в пределах от 2m,2 до 3m,5, а у второй—от 3m,3 до 14m,2?

Задача 335. Во сколько раз меняется визуальная и болометрическая светимость переменных звезд α Ориона и α Скорпиона, если у первой звезды визуальный блеск колеблется от 0m,4 до 1m,3 и Соответствующая ему болометрическая поправка от —3m,1 до —3m,4, а у второй звезды — блеск от 0m,9 до 1m,8 и болометрическая поправка от —2m,8 до —3m,0?

Задача 336. В каких пределах и во сколько раз меняются линейные радиусы переменных звезд α Ориона и α Скорпиона, если у первой звезды параллакс равен 0",005 и угловой радиус меняется от 0",034 (в максимуме блеска) до 0",047 (в минимуме блеска), а у второй — параллакс 0",019 и углавой радиус —от 0",028 до 0",040?

Задача 337. По данным задач 335 и 336 вычислить температуру Бетельгейзе и Антареса в максимуме их блеска, ес ли в минимуме температура первой звезды равна 3200К, а второй — 3300К.

Задача 338. Во сколько раз и с каким суточным градиентом меняется светимость в желтых и синих лучах переменных звезд-цефеид α Малой Медведицы, ζ Близнецов, η Орла, ΤΥ Щита и UZ Щита, сведения о переменности которых следующие:

Звезда	Период	Блеск в синих лучах	Основной показатель цвета
		в максимуме	в минимуме	в максимуме	в минимуме
α М. Медведицы ζ Близнецов η Орла ΤΥ Щита UΖ Щита	3д97 10,15 7,18 11,05 14,74	2m50 4,38 4,08 11,79 12,43	2m,66 5,18 5,36 13,19 13,80	+0m,56 +0,70 +0,59 + 1,47 + 1,63	+0m,61 + 1,02 + 1,04 +2,00 +2,12

Задача 339. По данным предыдущей задачи найти амплитуды изменения блеска (в желтых и синих лучах) и основных показателей цвета звезд, построить графики зависимости амплитуд от периода переменности и сформулировать вывод об обнаруженной по графикам закономерности.

Задача 340. В минимуме блеска визуальная звездная величина звезды δ Цефея 4m,3, а звезды R Треугольника 12m,6. Каков блеск этих звезд в максимуме светимости, если она у них возрастает соответственно в 2,1 и 760 раз?

Задача 341. Блеск Новой Орла 1918 г. изменился за 2,5 сут с 10m,5 до 1m,1. Во сколько раз он увеличился и как в среднем менялся на протяжении полусуток?

Задача 342. Блеск Новой Лебедя, обнаруженной 29 августа 1975 г., до вспышки был близок к 21m, а в максимуме увеличился до 1m,9. Если считать, что в среднем абсолютная звездная величина новых звезд в максимуме блеска бывает около —8m, то какую светимость имела эта звезда до вспышки и в максимуме блеска и на каком примерно расстоянии от Солнца звезда находится?

Задача 343. Эмиссионные водородные линии Н5 (4861 А), и Н1 (4340 А) в спектре Новой Орла 1918 г. были Смещены к фиолетовому концу соответственно на 39,8 Å и 35,6 Å, а в спектре Новой Лебедя 1975 г. — на 40,5 Å и 36,2 Å. С какой скоростью расширялись газовые оболочки, сброшенные этими звездами?

Задача 344. Угловые размеры галактики М81 в созвездии Большой Медведицы равны 35'Х14', а галактики М51 в созвездии Гончих Псов—14'Х10', Наибольший блеск сверхновых звезд, вспыхнувших в разное время в этих галактиках, был равен соответственно 12m,5 и 15m,1, Приняв в среднем абсолютную звездную величину сверхновых звезд в максимуме блеска близкой к —15m,0, вычислить расстояния до этих галактик и их линейные размеры.

Ответы - Кратные и переменные звезды