
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классификация моделей и задач в математическом программированииСодержание книги
Поиск на нашем сайте Примеры экономических задач 1) Задача оптимального распределения ресурсов при планировании выпуска продукции на предприятии (задача об ассортименте). Предположим, что предприятие выпускает n различных изделий. Для их производства требуются m различных видов ресурсов (сырья, вспомогательных материалов, рабочего и машинного времени). Эти ресурсы ограничены и составляют в планируемый период b 1, b 2, …, bm условных единиц. Известны также технологические коэффициенты aij, которые указывают, сколько единиц i -го ресур са требуется для производства изделия j -го вида (i = 1, m; j = 1, n). Пусть прибыль, получаемая предприятием при реализации едини цы изделия j -го вида, равна cj. В планируемый период все показа тели bi, aij и cj предполагаются постоянными. Требуется составить такой план выпуска продукции, при реа лизации которого прибыль предприятия была бы наибольшей. Другими словами, требуется составить о п т и м а л ь н ы й план работы предприятия X x x xn = (1, 2,...,), т.е. найти такие значения переменных x 1, x 2, …, xn (объем выпуска продукции каждого вида), чтобы обеспечить предприятию получение максимальной прибыли от реализации всей продукции и чтобы на ее производство хватило имеющихся в распоряжении ресурсов. 2) задача на максимум выпуска продукции При постановке задачи на максимум выпуска продукции при заданных ограничениях по ресурсам вводимые переменные и коэффициенты обычно имеют следующий смысл: Хj - выпуск продукции при использовании j-го технологического способа; Cj – цена единицы продукции при j-м способе производства; aij - расход i-го ресурса при j-м способе (коэффициенты материалоемкости, фондоемкости, трудоемкости); bi - наличие i-го ресурса. 3) задача о смесях (рационе, диете); К задачам о диете относятся задачи, в которых требуется выбрать самый дешевый пищевой рацион, содержащий необходимое количество указанных заранее питательных веществ. Предполагается, что: 1. известен перечень биологически необходимых питательных веществ и их минимальная норма (например, суточная); 2. задан набор продуктов, из которых требуется составить пищевой рацион; 3. имеются нормы содержания различных питательных веществ в единице соответствующего продукта; 4. известна цена единицы каждого продукта, который может быть использован в пищевом рационе. Подобная проблема возникает при выборе рационального корма для скота. 4) транспортная задача Транспортная задача — задача об оптимальном плане перевозок однородного продукта из однородных пунктов наличия в однородные пункты потребления на однородных транспортных средствах (предопределённом количестве) со статичными данными и линеарном подходе (это основные условия задачи). Для транспортной задачи выделяют два типа задач: критерий стоимости (достижение минимума затрат на перевозку) или расстояний и критерий времени (затрачивается минимум времени на перевозку). 5) задача о рациональном использовании имеющихся мощностей; Задача о назначениях Классификация моделей и задач в математическом программировании Математическое программирование используется для решения практических организационных задач. Задачи математического программирования находят применение в различных областях человеческой деятельности, где необходим выбор одного из возможных образов действий (программ действий). Значительное число задач, возникающих в обществе, связано с управляемыми явлениями, т. е. с явлениями, регулируемыми на основе сознательно принимаемых решений. При том ограниченном объеме информации, который был доступен на ранних этапах развития общества, принималось оптимальное в некотором смысле решение на основании интуиции и опыта, а затем, с возрастанием объема информации об изучаемом явлении, – с помощью ряда прямых расчетов. Так происходило, например, создание календарных планов работы промышленных предприятий.
Этапы решения экономических задач математическими методами 1-й этап. Построение качественной модели рассматриваемой проблемы, т. е. выделение факторов, которые представляются наиболее важными, и установление закономерностей, которым они подчиняются. Обычно этот этап выходит за пределы математики. 2-й этап. Построение математической модели рассматриваемой проблемы, т. е. запись в математических терминах качественной модели. Таким образом, математическая модель – это записанная в математических символах абстракция реального явления, так конструируемая, чтобы анализ ее давал возможность проникнуть в сущность явления. Математическая модель устанавливает соотношения между совокупностью переменных – параметрами управления явлением. Этот этап включает также построение целевой функции переменных, т. е. такой числовой характеристики, большему (или меньшему) значению которой соответствует лучшая ситуация с точки зрения принимающего решения. Итак, в результате этих двух этапов формируется соответствующая математическая задача. Причем, второй этап уже требует привлечения математических знаний. 3-й этап. Исследование влияния переменных на значение целевой функции. Этот этап предусматривает владение математическим аппаратом для решения математических, задач, возникающих на втором этапе процесса принятия, решения.Широкий класс задач управления составляют такие экстремальные задачи, в математических моделях которых условия на переменные задаются равенствами и неравенствами. Теория и методы решения этих задач как раз и составляют содержание математического программирования. На третьем этапе, пользуясь математическим аппаратом, находят решение соответствующих экстремальных задач. Обратим внимание на то, что задачи математического программирования, связанные с решением практических вопросов, как правило, имеют большое число переменных и ограничений. Объем вычислительных работ для нахождения соответствующих решений столь велик, что весь процесс не мыслится без применения современных электронных вычислительных машин (ЭВМ), а значит, требует либо создания программ для ЭВМ, реализующих те или иные алгоритмы, либо использования уже имеющихся стандартных программ. 4-й этап. Сопоставление результатов вычислений, полученных на 3-м этапе, с моделируемым объектом, т. е. экспертная проверка результатов (критерий практики). Таким образом, на этом этапе устанавливается степень адекватности модели и моделируемого объекта в пределах точности исходной информации. Принципы построения экономико-математичеких моделей 1. Принцип достаточности исходной информации. В каждой модели должна использоваться только та информация, которая известна с точностью, требуемой для получения реультатов моделирования. 2. Принцип инвариантности (однозначности) информации требует, чтобы входная информация, используемая в модели, была независима от тех параметров моделируемой системы, которые еще неизвестны на данной стадии исследования. 3. Принцип преемственности. Сводится к тому, что каждая последующая модель не должна нарушать свойств объекта, установленных или отраженных в предыдущих моделях. 4. Принцип эффективной реализуемости. Необходимо, чтобы модель могла быть реализована при помощи современных вычислительных средств.
... am1x1+am2x2+…+amnxn=bm xj≥0; j=1…n bi≥0; i=1…m Замечание. Если какая-либо правая часть отрицательная, то это уравнение нужно умножить на -1. Любую задачу можно представить в векторной форме. АХ=В, где Решение, удовлетворяющее всем ограничениям и условиям неотрицательности, называется допустимым. Множество всех допустимых решений образуют область допустимых решений (ОДР). Допустимое решение, доставляющее мин. или макс. целевой функции называется оптимальным решением. Матрица А, составленная из коэффициентов при неизвестных называется матрицей условий. Вектор столбец А0=
Замечание. Нахождение оптимального решения может вызвать затруднение с перебором всех опорных решений когда задача имеет бесконечное множество решений или решение отсутствует. По этому вводят специальный параметр θ. Построение начального опорного решения. Необходимо в каждом уравнении системы найти базисную переменную (которая входит только в одно уравнение с коэффициентом +1). Обозначаю базисную переменную хiб. х1б – базисная переменная первого уравнения и т.д. Составляется первая симплекс-таблица следующим образом.
Где Сiб коэффициент из целевой функции при соответствующей базисной переменной. xjб – базисная переменная из соответствующего уравнения. bi – свободные члены системы. В верхнюю строчку над х выписывают все коэффициенты из целевой функции. Последнюю строчку называют проверочной. Элементы, входящие в эту строку называются оценками переменных. Столбец А0 в результате показывает значение целевой функции начального опорного решения.
Критерий оптимальности Проверка на оптимальность опорного плана проходит с помощью критерия оптимальности, переход к другому опорному плану — с помощью преобразований Жордана-Гаусса и с использованием критерия оптимальности. Полученный опорный план снова проверяется на оптимальность и т.д. Процесс заканчивается за конечное число шагов, причем на последнем шаге либо выявляется неразрешимость задачи (конечного оптимума нет), либо получаются оптимальный опорный план и соответствующее ему оптимальное значение целевой функции. Признак оптимальности заключается в следующих двух теоремах. Теорема 1. Если для некоторого вектора, не входящего в базис, выполняется условие:
то можно получить новый опорный план, для которого значение целевой функции будет больше исходного; при этом могут быть два случая: если все координаты вектора, подлежащего вводу в базис, неположительны, то задача линейного программирования не имеет решения; если имеется хотя бы одна положительная координата у вектора, подлежащего вводу в базис, то можно получить новый опорный план. Теорема 2. Если для всех векторов выполняется условие
13. алгоритм стандартного симплекс методоа
14. Рассматривая симплекс-метод, мы предполагали, что задача линейного программирования является невырожденной, т.е. каждый опорный план содержит ровно m положительных компонент, где m - число ограничений в задаче. В вырожденном опорном плане число положительных компонент оказывается меньше числа ограничений: некоторые базисные переменные, соответствующие данному опорному плану, принимают нулевые значения. Используя геометрическую интерпретацию для простейшего случая, когда n - m = 2 (число небазисных переменных равно 2), легко отличить вырожденную задачу от невырожденной. В вырожденной задаче в одной вершине многогранника условий пересекается более двух прямых, описываемых уравнениями вида xi = 0. Это значит, что одна или несколько сторон многоугольника условий стягиваются в точку. Опорный план называется невырожденным, если он содержит ровно т положительных компонент, в противном случае он называется вырожденным. Если при соблюдении условия допустимости для исключения из базиса можно выбрать более чем 1 вариант, то следующая итерация симплекс метода приведёт к вырожденному решению, когда одна из базисных переменных равна нулю. Последующие итерации могут не привести к улучшению значений целевой функции и становится возможным бесконечное повторение одной и той же последовательности итераций, не улучшающих решение. Такая ситуация называется зацикливанием. Чтобы обеспечивать единственность выбора выводимого вектора, исходя из условий допустимости, разработано несколько специальных приёмов.
Теоремы двойственности. Любой задаче линейного программирования можно поставить в соответствие другую задачу, которую называют двойственной или сопряжённой. Двойственные задачи бывают симметричными и несимметричными. Теорема 1. Если одна из пары двойственных задач имеет оптимальное решение, то двойственная к ней имеет оптимальное решение, при чём значение целевой функции на своих оптимальных решениях совпадают. Если же одна из пары двойственных задач не имеет решения, то и другая также не имеет решения. Теорема 2. Для того чтобы допустимое решение исходной задачи являлось оптимальным решением необходимо и достаточно, чтобы при подстановке оптимального решения в систему ограничений исходной задачи выполнялось как строгое неравенство. И тогда при этом i-тая координата оптимального решения двойственной задачи равна 0. Если же i-тая координата оптимального решения двойственной задачи отлична от 0, то i-тое ограничение исходной задачи удовлетворяется как равенство.
Теорема двойственности Для существования оптимального плана любой из пары двойственных задач необходимо и достаточно существование допустимого плана для каждой из них. Если одна из двойственных задач имеет оптимальное решение, то и другая имеет оптимальное решение, причем экстремальные значения целевых функций равны: Экономическое содержание первой теоремы двойственности состоит в следующем: если задача определения оптимального плана, максимизирующего выпуск продукции, разрешима, то разрешима и задача определения оценок ресурсов. Причем цена продукции, полученной при реализации оптимального плана, совпадает с суммарной оценкой ресурсов. Совпадение значений целевых функций для соответствующих планов пары двойственных задач достаточно для того, чтобы эти планы были оптимальными. Это значит, что план производства и вектор оценок ресурсов являются оптимальными тогда и только тогда, когда цена произведенной продукции и суммарная оценка ресурсов совпадают. Оценки выступают как инструмент балансирования затрат и результатов. Двойственные оценки, обладают тем свойством, что они гарантируют рентабельность оптимального плана, т. е. равенство общей оценки продукции и ресурсов, и обусловливают убыточность всякого другого плана, отличного от оптимального. Двойственные оценки позволяют сопоставить и сбалансировать затраты и результаты системы.
19. Оценки как мера дефицитности ресурсов. Двойственные оценки отражают сравнительную дефицитность факторов производства. Чем выше величина оценки Свойство 2. Оценки как мера влияния ограничений на значение целевой функции. Величина двойственной оценки какого-либо ресурса показывает, насколько возросло бы максимальное значение целевой функции, если бы объем данного ресурса увеличился на единицу. В связи с этим значение объективно обусловленной оценки иногда называют теневой ценой ресурса. Теневая цена - это стоимость единицы ресурса в оптимальном решении. Однако нужно учитывать, что двойственные оценки позволяют измерить эффективность лишь незначительного изменения объема ресурсов. При значительных изменениях может быть получен новый оптимальный план и новые двойственные оценки.
Свойство 3. Оценки как инструмент определения эффективности отдельных хозяйственных решений. С помощью двойственных оценок можно определить выгодность выпуска новых изделий, эффективность новых технологических способов производства. При этом эффективным может считаться тот вариант производства, для которого сумма прибыли, недополученной из-за отвлечения дефицитных ресурсов, будет меньше прибыли получаемой. Разница между этими величинами (Δj) вычисляется как:
В том случае, если Δj ≤ 0, вариант производства является выгодным, если Δj > 0 – вариант невыгоден.
20. Третья теорема двойственности позволяет определить зависимость изменения целевой функции начальной задачи от изменения запасов "ресурсов": (В формулировке для несимметричной двойственной задачи) Если i-ая компонента
Если i-ая компонента оптимального плана исходной задачи равна нулю, то i-ое ограничение двойственной задачи при подстановке в нее оптимального плана имеет вид
Доказательство. Еще раз вспомним симплекс-метод и симплекс-таблицу для оптимального плана. Там получалось, что если Но. согласно предыдущей теореме,
Теорема доказана. Отметим в заключение, что для симметричных двойственных задач эта теорема звучит так: Теорема 3. (В формулировке для симметричной двойственной задачи). Если i-ая компонента оптимального плана какой-то задачи положительна, то i-ое ограничение двойственной ей задачи, при подстановке в не оптимального плана, превращается в строгое равенство. Наоборот, если i-ое ограничение какой-то задачи, при подстановке в него оптимального плана, превращается в строгое неравенство, то i-ая компонента оптимального плана двойственной ей задачи равна нулю. Модели транспортной задачи Открытая модель решается приведением к закрытой модели. 22.Методы построения начального опорного решения. Метод потенциалов Циклом в транспортной таблице называется несколько клеток, соединенных замкнутой ломаной линией, которая в каждой клетке совершает поворот на 90, Знаком " + " отмечают те вершины, в которых перевозки увеличиваются, а знаком "- " - те вершины, в которых перевозки уменьшаются. Перемещение какого-то количества единиц груза по циклу означает увеличение перевозок на это количество единиц в положительных вершинах и уменьшение перевозок на это же количество единиц в отрицательных вершинах. При этом, если перевозки остаются неотрицательными, план остается допустимым. Стоимость плана при этом может меняться. Ценой цикла называется увеличение стоимости перевозок при перемещении единицы груза по этому циклу. Очевидно, цена цикла равна алгебраической сумме стоимостей, стоящих в вершинах цикла, при этом стоимости в положительных вершинах берутся со знаком " +", а стоимости в отрицательных вершинах берутся со знаком " - ". Идея метода потенциалов состоит в следующем. Для любой свободной клетки транспортной таблицы всегда существует единственный цикл, положительная вершина которого лежит в этой свободной клетке, а все остальные - в базисных. Если цена такого цикла отрицательна, то план можно улучшить перемещением перевозок по данному циклу. Количество единиц груза, которое можно переместить, определяется минимальным значением перевозок, стоящих в отрицательных вершинах цикла (если переместить большее число единиц груза, возникнут отрицательные перевозки). Если циклов с отрицательной ценой нет, то это означает, что дальнейшее улучшение плана невозможно, т.е. оптимальный план найден. Вычислительная схема метода потенциалов Шаг 1. Строим опорный план (методом северо-западного угла) с n+m-1 базисными клетками. Шаг 2. Определяем платежи для всех базисных клеток. Один из платежей (например a1) полагаем равньм нулю. Шаг 3. Считаем псевдостоимости для всех клеток, то план оптимален. Вычисляем значение целевой функции L на этом плане и исследования прекращаем. Шаг 4. Если есть свободная клетка, для которой
24Транспортная задача с ограничениями на пропускную способность.
25.Транспортная задача по критерию времени.
Задача о назначениях. ЗАДАЧА О НАЗНАЧЕНИЯХ [assignment problem] — вид задачи линейного программирования, с помощью которой решаются вопросы типа: как распределить рабочих по станкам, чтобы общая выработка была наибольшей или затраты на заработную плату наименьшими (поскольку для каждой комбинации “рабочий — станок” характерна своя производительность труда), как наилучшим образом распределить экипажи самолетов, как назначить людей на различные должности (отсюда и название задачи) и т. д. Математически такие задачи — частный случай распределительных задач с той особенностью, что в них объемы наличных и требующихся для выполнения каждой работы ресурсов равны единице, т. е. aj = bj = 1, и все xij=1, если работник i назначен на работу j, или нулю в остальных случаях (обозначения см. в ст. “Распределительные задачи”). Иначе говоря, для выполнения каждой работы расходуется только один вид ресурса, а каждый ресурс может быть использован на одной работе: ресурсы неделимы между работами, а работы — между ресурсами. Исходные данные группируются в таблице, которая называется матрицей оценок, результаты — в матрице назначений. Количество возможных вариантов назначений равно факториалу числа работ и ресурсов и огромно даже в небольшой зада
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 445; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.018 с.) |

 называют решением или планом задачи.
называют решением или планом задачи. из свободных членов называется вектором правых частей.
из свободных членов называется вектором правых частей.


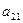



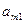



 , где
, где  ,
, 
 , то полученный план является оптимальным.
, то полученный план является оптимальным. . Если одна из двойственных задач неразрешима вследствие неограниченности целевой функции на множестве допустимых решений, то система ограничений другой задачи противоречива.
. Если одна из двойственных задач неразрешима вследствие неограниченности целевой функции на множестве допустимых решений, то система ограничений другой задачи противоречива. , тем выше дефицитность i-го ресурса. Факторы, получившие нулевые оценки, не являются дефицитными и не ограничивают производство.
, тем выше дефицитность i-го ресурса. Факторы, получившие нулевые оценки, не являются дефицитными и не ограничивают производство.
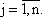
 оптимального плана исходной задачи строго положительна, то i-ое ограничение двойственной задачи при подстановке в нее оптимального плана превращается в строгое равенство
оптимального плана исходной задачи строго положительна, то i-ое ограничение двойственной задачи при подстановке в нее оптимального плана превращается в строгое равенство .
. .
. , то
, то  , если же
, если же  , то
, то  .
. ,то есть
,то есть  есть i-ая строка матрицы
есть i-ая строка матрицы  . Опять же, при доказательстве предыдущей теоремы было получено соотношение
. Опять же, при доказательстве предыдущей теоремы было получено соотношение ,
,
 .
.

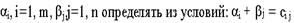
 для всех свободных клеток. Если
для всех свободных клеток. Если 
 то улучшаем план, перебрасывая перевозки по циклу этой свободной клетки. Шаг 5. Возвращаемся к шагу 2 для пересчета платежей нового опорного плана.
то улучшаем план, перебрасывая перевозки по циклу этой свободной клетки. Шаг 5. Возвращаемся к шагу 2 для пересчета платежей нового опорного плана.


