
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Симметричные двойственные задачи и правила их построения.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Любой задаче линейного программирования можно поставить в соответствие другую задачу, которую называют двойственной или сопряжённой. Например, составить двойственную задачу к задаче использования ресурсов. Имеется m видов сырья в количестве b1, b2, …, bm, которые используют для изготовления n видов продукции. Известно, что на единицу каждого вида продукции расходуется aij количество сырья, где i= Математическая модель данной задачи имеет вид: Z(x)=C1x1+C2x2+…+Cnxn → max
xj≥0; j= Предположим, что второй производитель хочет перекупить сырьё. Составим двойственную задачу, решение которой позволит определить условие продажи сырья. Введём цены видов сырья: I=y1, II=y2, …, N=ym. Затраты на приобретение i-того вида сырья в количестве bi=biyi. Второму производителю выгодно минимизировать суммарные затраты на приобретение всех видов сырья. По этому целевая функция задачи имеет вид: F(y)=b1y1+b2y2+…+bmym → min Первому производителю не выгодно продать сырьё, если суммарная стоимость всех видов сырья, расходуемых на каждое изделие j-той продукции a1jy1+a2jy2+…+amjym≤Cj. Тогда система ограничений задачи имеет вид.
yj≥0; j= Связь исходной и двойственной задач состоит в том, что коэффициенты Cj исходной задачи являются свободными членами системы ограничений двойственной задачи. А свободные члены системы ограничений исходной задачи служат коэффициентами целевой функции двойственной задачи. Матрица коэффициентов системы ограничений двойственной задачи является транспонированной матрицей коэффициентов системы ограничений исходной задачи. Двойственные задачи бывают симметричными и несимметричными. Симметричные пары: 1)если Z(x) → max, Ах≤А0, х≥0, то F(y) =YA0→ min, YA≥С, y≥0; 2)если Z(x) → min, Ах≥А0, х≥0, то F(y) =YA0→ max, y≥0. Общие правила составления двойственных задач: 1)Во всех ограничения исходной задачи свободные члены должны находится в правой части, а члены с независимыми – в левой. 2)Ограничения неравенства исходной задачи должны быть записаны так, чтобы знаки неравенств у них были направлены в одну сторону. 3)Если знаки неравенств в исходной задаче ≤, то целевая функция должна стремится к максимуму, если знаки ≥, то должна стремится к минимуму. 4)Целевая функция двойственной задачи F(y)=с0+b1y1+b2y2+…+bmyn → min, где с0 – свободный член целевой функции Z(x). 5)Целевая функция F(y) должна оптимизироваться противоположным, по сравнению с Z(x), образом. 6)Каждому неизвестному xj исходной задачи соответствует ограничение в двойственной задаче.
Теоремы двойственности. Любой задаче линейного программирования можно поставить в соответствие другую задачу, которую называют двойственной или сопряжённой. Двойственные задачи бывают симметричными и несимметричными. Теорема 1. Если одна из пары двойственных задач имеет оптимальное решение, то двойственная к ней имеет оптимальное решение, при чём значение целевой функции на своих оптимальных решениях совпадают. Если же одна из пары двойственных задач не имеет решения, то и другая также не имеет решения. Теорема 2. Для того чтобы допустимое решение исходной задачи являлось оптимальным решением необходимо и достаточно, чтобы при подстановке оптимального решения в систему ограничений исходной задачи выполнялось как строгое неравенство. И тогда при этом i-тая координата оптимального решения двойственной задачи равна 0. Если же i-тая координата оптимального решения двойственной задачи отлична от 0, то i-тое ограничение исходной задачи удовлетворяется как равенство.
Теорема двойственности Для существования оптимального плана любой из пары двойственных задач необходимо и достаточно существование допустимого плана для каждой из них. Если одна из двойственных задач имеет оптимальное решение, то и другая имеет оптимальное решение, причем экстремальные значения целевых функций равны: Экономическое содержание первой теоремы двойственности состоит в следующем: если задача определения оптимального плана, максимизирующего выпуск продукции, разрешима, то разрешима и задача определения оценок ресурсов. Причем цена продукции, полученной при реализации оптимального плана, совпадает с суммарной оценкой ресурсов. Совпадение значений целевых функций для соответствующих планов пары двойственных задач достаточно для того, чтобы эти планы были оптимальными. Это значит, что план производства и вектор оценок ресурсов являются оптимальными тогда и только тогда, когда цена произведенной продукции и суммарная оценка ресурсов совпадают. Оценки выступают как инструмент балансирования затрат и результатов. Двойственные оценки, обладают тем свойством, что они гарантируют рентабельность оптимального плана, т. е. равенство общей оценки продукции и ресурсов, и обусловливают убыточность всякого другого плана, отличного от оптимального. Двойственные оценки позволяют сопоставить и сбалансировать затраты и результаты системы.
19. Оценки как мера дефицитности ресурсов. Двойственные оценки отражают сравнительную дефицитность факторов производства. Чем выше величина оценки Свойство 2. Оценки как мера влияния ограничений на значение целевой функции. Величина двойственной оценки какого-либо ресурса показывает, насколько возросло бы максимальное значение целевой функции, если бы объем данного ресурса увеличился на единицу. В связи с этим значение объективно обусловленной оценки иногда называют теневой ценой ресурса. Теневая цена - это стоимость единицы ресурса в оптимальном решении. Однако нужно учитывать, что двойственные оценки позволяют измерить эффективность лишь незначительного изменения объема ресурсов. При значительных изменениях может быть получен новый оптимальный план и новые двойственные оценки.
Свойство 3. Оценки как инструмент определения эффективности отдельных хозяйственных решений. С помощью двойственных оценок можно определить выгодность выпуска новых изделий, эффективность новых технологических способов производства. При этом эффективным может считаться тот вариант производства, для которого сумма прибыли, недополученной из-за отвлечения дефицитных ресурсов, будет меньше прибыли получаемой. Разница между этими величинами (Δj) вычисляется как:
В том случае, если Δj ≤ 0, вариант производства является выгодным, если Δj > 0 – вариант невыгоден.
20. Третья теорема двойственности позволяет определить зависимость изменения целевой функции начальной задачи от изменения запасов "ресурсов": (В формулировке для несимметричной двойственной задачи) Если i-ая компонента
Если i-ая компонента оптимального плана исходной задачи равна нулю, то i-ое ограничение двойственной задачи при подстановке в нее оптимального плана имеет вид
Доказательство. Еще раз вспомним симплекс-метод и симплекс-таблицу для оптимального плана. Там получалось, что если Но. согласно предыдущей теореме,
Теорема доказана. Отметим в заключение, что для симметричных двойственных задач эта теорема звучит так: Теорема 3. (В формулировке для симметричной двойственной задачи). Если i-ая компонента оптимального плана какой-то задачи положительна, то i-ое ограничение двойственной ей задачи, при подстановке в не оптимального плана, превращается в строгое равенство. Наоборот, если i-ое ограничение какой-то задачи, при подстановке в него оптимального плана, превращается в строгое неравенство, то i-ая компонента оптимального плана двойственной ей задачи равна нулю. Модели транспортной задачи Открытая модель решается приведением к закрытой модели. 22.Методы построения начального опорного решения. Метод потенциалов Циклом в транспортной таблице называется несколько клеток, соединенных замкнутой ломаной линией, которая в каждой клетке совершает поворот на 90, Знаком " + " отмечают те вершины, в которых перевозки увеличиваются, а знаком "- " - те вершины, в которых перевозки уменьшаются. Перемещение какого-то количества единиц груза по циклу означает увеличение перевозок на это количество единиц в положительных вершинах и уменьшение перевозок на это же количество единиц в отрицательных вершинах. При этом, если перевозки остаются неотрицательными, план остается допустимым. Стоимость плана при этом может меняться. Ценой цикла называется увеличение стоимости перевозок при перемещении единицы груза по этому циклу. Очевидно, цена цикла равна алгебраической сумме стоимостей, стоящих в вершинах цикла, при этом стоимости в положительных вершинах берутся со знаком " +", а стоимости в отрицательных вершинах берутся со знаком " - ". Идея метода потенциалов состоит в следующем. Для любой свободной клетки транспортной таблицы всегда существует единственный цикл, положительная вершина которого лежит в этой свободной клетке, а все остальные - в базисных. Если цена такого цикла отрицательна, то план можно улучшить перемещением перевозок по данному циклу. Количество единиц груза, которое можно переместить, определяется минимальным значением перевозок, стоящих в отрицательных вершинах цикла (если переместить большее число единиц груза, возникнут отрицательные перевозки). Если циклов с отрицательной ценой нет, то это означает, что дальнейшее улучшение плана невозможно, т.е. оптимальный план найден. Вычислительная схема метода потенциалов Шаг 1. Строим опорный план (методом северо-западного угла) с n+m-1 базисными клетками. Шаг 2. Определяем платежи для всех базисных клеток. Один из платежей (например a1) полагаем равньм нулю. Шаг 3. Считаем псевдостоимости для всех клеток, то план оптимален. Вычисляем значение целевой функции L на этом плане и исследования прекращаем. Шаг 4. Если есть свободная клетка, для которой
24Транспортная задача с ограничениями на пропускную способность.
25.Транспортная задача по критерию времени.
Задача о назначениях. ЗАДАЧА О НАЗНАЧЕНИЯХ [assignment problem] — вид задачи линейного программирования, с помощью которой решаются вопросы типа: как распределить рабочих по станкам, чтобы общая выработка была наибольшей или затраты на заработную плату наименьшими (поскольку для каждой комбинации “рабочий — станок” характерна своя производительность труда), как наилучшим образом распределить экипажи самолетов, как назначить людей на различные должности (отсюда и название задачи) и т. д. Математически такие задачи — частный случай распределительных задач с той особенностью, что в них объемы наличных и требующихся для выполнения каждой работы ресурсов равны единице, т. е. aj = bj = 1, и все xij=1, если работник i назначен на работу j, или нулю в остальных случаях (обозначения см. в ст. “Распределительные задачи”). Иначе говоря, для выполнения каждой работы расходуется только один вид ресурса, а каждый ресурс может быть использован на одной работе: ресурсы неделимы между работами, а работы — между ресурсами. Исходные данные группируются в таблице, которая называется матрицей оценок, результаты — в матрице назначений. Количество возможных вариантов назначений равно факториалу числа работ и ресурсов и огромно даже в небольшой задаче. Поэтому для нахождения оптимального варианта применяют специальные алгоритмы. Среди них особенно эффективен при решении З. о н. вручную т. н. венгерский метод. Наиболее эффективным методом ее решения является венгерский метод. Задача о назначениях имеет много интерпретаций: распределение работ между механизмами, распределение целей между огневыми средствами для максимизации математического ожидания числа пораженных целей или среднего ущерба и т.д. Данная задача решается с помощью алгоритма, носящего название "Венгерского метода", состоящего из 3 этапов: 1 этап: 1 Формализация проблемы в виде транспортной таблицы 2 В каждой строке таблицы найти наименьший элемент и вычесть его из всех элементов данной строки 3 Повторить ту же процедуру для столбцов Задачей является распределение всех подлежащих назначению единиц в клетки с нулевой стоимостью. Оптимальное значение целевой функции в этом случае равно нулю. 2 этап: 1 Найти строку, содержащую только одно нулевое значение, в его клетку помещается один элемент (0 обводится квадратиком). Если такие строки отсутствуют, допустимо начать с любой строки. 2 Зачеркнуть оставшиеся нулевые значения данного столбца 3 Повторять пп.1-2, пока продолжение указанной процедуры окажется невозможным Если окажется, что имеется несколько нулей, которым не соответствуют назначения, и которые остались незачеркнутыми, необходимо: 4 Найти столбец, содержащий только одно нулевое значение, в его клетку помещается один элемент. 5 Зачеркнуть оставшиеся нули в данной строке 6 Повторять пп.4-5, пока продолжение указанной процедуры окажется невозможным Если выяснится, что таблица содержит неучтенные нули - повторить пп. 1-6 Если решение является допустимым, оно оптимально. Если нет - перейти к этапу 3. 3 этап: (Если решение является недопустимым) 1 Провести минимальное количество прямых через столбцы и строки матрицы таким образом, чтобы они проходили через все нули, содержащиеся в таблице 2 Найти наименьший из элементов, через которые не проходит ни одна прямая 3 Вычесть его из всех элементов, через которые не проходят прямые 4 Прибавить его ко всем элементам, лежащим на пересечении прямых 5 Элементы, через которые проходит только одна прямая, оставить неизменными В результате в таблице появится как минимум одно новое нулевое значение. Вернуться к этапу 2 и повторить решение заново.
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 592; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.7.53 (0.012 с.) |

 , j=
, j=  . Пусть Cj – прибыль при реализации j-того вида продукции.
. Пусть Cj – прибыль при реализации j-того вида продукции.

 . Если одна из двойственных задач неразрешима вследствие неограниченности целевой функции на множестве допустимых решений, то система ограничений другой задачи противоречива.
. Если одна из двойственных задач неразрешима вследствие неограниченности целевой функции на множестве допустимых решений, то система ограничений другой задачи противоречива. , тем выше дефицитность i-го ресурса. Факторы, получившие нулевые оценки, не являются дефицитными и не ограничивают производство.
, тем выше дефицитность i-го ресурса. Факторы, получившие нулевые оценки, не являются дефицитными и не ограничивают производство.
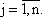
 оптимального плана исходной задачи строго положительна, то i-ое ограничение двойственной задачи при подстановке в нее оптимального плана превращается в строгое равенство
оптимального плана исходной задачи строго положительна, то i-ое ограничение двойственной задачи при подстановке в нее оптимального плана превращается в строгое равенство .
. .
. , то
, то  , если же
, если же  , то
, то  .
. ,то есть
,то есть  есть i-ая строка матрицы
есть i-ая строка матрицы  . Опять же, при доказательстве предыдущей теоремы было получено соотношение
. Опять же, при доказательстве предыдущей теоремы было получено соотношение ,
,
 .
.

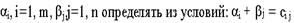
 для всех свободных клеток. Если
для всех свободных клеток. Если 
 то улучшаем план, перебрасывая перевозки по циклу этой свободной клетки. Шаг 5. Возвращаемся к шагу 2 для пересчета платежей нового опорного плана.
то улучшаем план, перебрасывая перевозки по циклу этой свободной клетки. Шаг 5. Возвращаемся к шагу 2 для пересчета платежей нового опорного плана.


