
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Необхідні умови існування сідлової точкиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для розробки методів розв’язування окремих типів задач нелінійного програмування важливе значення має поняття сідлової точки, а також визначення необхідних і достатніх умов існування сідлових точок функції Лагранжа Розглянемо нелінійну здачу:
Причому на компоненти векторів Функція Лагранжа для цієї задачі має вигляд: Точка Для диференційованих функцій Сідлова точка
Нерівність виконується для всіх точок Оскільки права частина нерівності є фіксована а в лівій частині змінюється лише одна координата Розглянемо спочатку випадок Можливі наступні випадки: 1) коли всі 2)коли точка максимуму функції L(xk) досягатиметься в точці
коли точка максимуму функції L(xk) досягатиметься також в точці Узагальнюючи всі три ситуації маємо:
Розглядаючи другу частину нерівності (4.43)
аналогічними міркуваннями, що проілюстровані рис. 5.14.-5.16. встановлюються необхідні умови для похідних по Об’єднуючи всі три випадки для невід’ємних координат, маємо необхідні умови сідлової точки:
Зауважимо, що для
І нарешті, як відомо з попереднього параграфа, якщо на знак
Узагальнення всіх випадків приводить до рівняння: Розглядаючи другу частину нерівності (5.43) за допомогою аналогічних міркувань встановлюємо необхідні умови для похідних по
Отже справджується рівняння: Сукупність співвідношень (5.44)-(5.51) становить необхідні умови, які повинна задовольняти сідлова точка
Теорема Куна-Таккера Розглянутий метод множників Лагранжа дає можливість знаходити лише локальні сідлові точки функції Лагранжа. Теорема Куна-Таккера дає можливість встановити типи задач для яких на множині допустимих розв’язків локальний екстремум є і глобальним екстремумом зумовленого типу. Теорема Куна-Таккера тісно пов’язана з необхідними та достатніми умовами існування сідлової точки. Розглянемо задачу нелінійного програмування, яку, не зменшуючи загальності, представимо у вигляді:
(Очевидно знак нерівності можна змінити на протилежний множенням лівої і правої частини обмеження на (-1)). Теорема 5.1. (Теорема Куна-Таккера). Вектор
і функція Доведення. Необхідність. Нехай
Розглянемо тепер вектор З умови (5.51) маємо
Для точки з координатами
Функція Для встановлення нерівності, що відповідає лівій частині умови (5.43), а саме
Отже у точці Достатність. Для доведення достатності умови теореми потрібно з того, що У (5.43) підставимо вираз функції Лагранжа (5.42) для задачі (5.52)-(5.53):
при всіх значеннях Розглянемо праву частину подвійної нерівності (5.56).
Остання нерівність має виконуватися для всіх
Тоді з лівої частини нерівності (5.56) маємо:
Так як Отже, точка Умови теореми Куна-Таккера виконуються лише для задач, що містять опуклі функції.
|
||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 578; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.72.78 (0.011 с.) |

 в (n+m)- вимірному просторі змінних
в (n+m)- вимірному просторі змінних 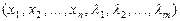 при довільних умовах, які можуть накладатися на їх знаки (необхідні і достатні умови існування сідлової точки функції Лагранжа при відсутності обмежень на знаки змінних розглянуто в § 5.12).
при довільних умовах, які можуть накладатися на їх знаки (необхідні і достатні умови існування сідлової точки функції Лагранжа при відсутності обмежень на знаки змінних розглянуто в § 5.12).
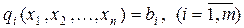
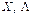 накладено обмеження по знаку. Позначимо множину точок, що задовольняють такі обмеження
накладено обмеження по знаку. Позначимо множину точок, що задовольняють такі обмеження  .
. =
= 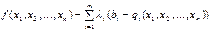 (5.42)
(5.42)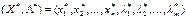 називається сідловою точкою функції Лагранжа (5.42), якщо для всіх
називається сідловою точкою функції Лагранжа (5.42), якщо для всіх  виконується співвідношення
виконується співвідношення 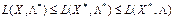 (5.43)
(5.43)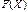 та
та 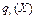 знайдемо необхідні умови існування сідлової точки.
знайдемо необхідні умови існування сідлової точки. функції
функції  виду (5.42) за означенням задовольняє умову:
виду (5.42) за означенням задовольняє умову:
 , тобто також і для тих у яких лише одна координата відрізняється від
, тобто також і для тих у яких лише одна координата відрізняється від  . Припустимо, що це
. Припустимо, що це  , а всі інші співпадають з координатами сідлової точки
, а всі інші співпадають з координатами сідлової точки  .
. , яку можна зобразити графічно на координатній площині.
, яку можна зобразити графічно на координатній площині. , тобто лише частину координатної площини для якої
, тобто лише частину координатної площини для якої  .
. максимальне значення функції L(xk) досягатиметься в точці для якої
максимальне значення функції L(xk) досягатиметься в точці для якої  (рис.5.11).
(рис.5.11). і розглядувана частинна похідна також дорівнюватиме нулю:
і розглядувана частинна похідна також дорівнюватиме нулю:  (рис. 5.12).
(рис. 5.12). , а частинна похідна
, а частинна похідна 
 для
для  , та
, та 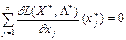 .
.
 функції Лагранжа в сідловій точці.
функції Лагранжа в сідловій точці. 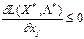 для тих індексів j де
для тих індексів j де  (5.44)
(5.44) маємо ті самі випадки, які зображено на мал. 5.11.-5.16, причому графіки будуть симетрично відображені відносно осі Оy, тобто для недодатних координат необхідна умова має вигляд:
маємо ті самі випадки, які зображено на мал. 5.11.-5.16, причому графіки будуть симетрично відображені відносно осі Оy, тобто для недодатних координат необхідна умова має вигляд: для тих індексів j де
для тих індексів j де  (5.45)
(5.45) умов не накладається, то необхідна умова
умов не накладається, то необхідна умова ,
,  – довільного знаку (5.46)
– довільного знаку (5.46) (5.47)
(5.47)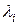 функції Лагранжа в сідловій точці:
функції Лагранжа в сідловій точці: для тих індексів і де
для тих індексів і де 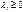 , (5.48)
, (5.48)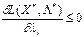 для тих індексів і де
для тих індексів і де  , (5.49)
, (5.49)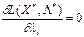 для тих індексів і де
для тих індексів і де  має довільний знак (5.50)
має довільний знак (5.50) (5.51)
(5.51)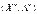 функції Лагранжа для точок, що належать множині
функції Лагранжа для точок, що належать множині  . При цьому
. При цьому  повинна мати частинні похідні по всіх компонентах векторів
повинна мати частинні похідні по всіх компонентах векторів  .
. (5.52)
(5.52) (5.53)
(5.53) (5.54)
(5.54) є оптимальним розв’язком задачі (5.52)-(5.54) тоді і тільки тоді, коли існує такий вектор
є оптимальним розв’язком задачі (5.52)-(5.54) тоді і тільки тоді, коли існує такий вектор  , що при
, що при  для всіх
для всіх 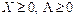 пара
пара 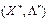 є сідловою точкою функції Лагранжа
є сідловою точкою функції Лагранжа ,
, є для всіх
є для всіх  угнута, а функції
угнута, а функції  – опуклі.
– опуклі. – оптимальний план задачі (5.52)-(5.53), тобто визначає точку глобального максимуму задачі. Отже для всіх інших планів задачі
– оптимальний план задачі (5.52)-(5.53), тобто визначає точку глобального максимуму задачі. Отже для всіх інших планів задачі  з множини допустимих розв’язків виконуватиметься співвідношення:
з множини допустимих розв’язків виконуватиметься співвідношення:
 , що відповідає точці глобального максимуму
, що відповідає точці глобального максимуму  і значення функції Лагранжа в точках
і значення функції Лагранжа в точках  ,
,  ,
,  де
де 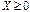 довільний план задачі з множини допустимих розв’язків,
довільний план задачі з множини допустимих розв’язків,  – вектор множників Лагранжа, що відповідає Х.
– вектор множників Лагранжа, що відповідає Х. , тоді
, тоді (5.55)
(5.55) деякі доданки виду
деякі доданки виду  можуть бути відмінні від нуля. Оскільки за умовою задачі
можуть бути відмінні від нуля. Оскільки за умовою задачі  , то лише при умові, що
, то лише при умові, що  матимемо нерівність:
матимемо нерівність: .
. – лінійна відносно
– лінійна відносно  , тобто остання нерівність виконується для будь-якого
, тобто остання нерівність виконується для будь-якого  . Отже точка
. Отже точка  – точка глобального мінімуму по
– точка глобального мінімуму по  скористаємося також рівнянням (5.51), просумувавши його по і:
скористаємося також рівнянням (5.51), просумувавши його по і:  . За умовою теореми
. За умовою теореми  – угнуті функції і
– угнуті функції і  , тому виконується наступне рівняння:
, тому виконується наступне рівняння:

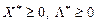 ,
, 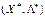 – сідлова точка функції
– сідлова точка функції  (тобто для
(тобто для 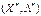 виконується (5.43)) довести, що тоді
виконується (5.43)) довести, що тоді  – є оптимальний план задачі опуклого програмування.
– є оптимальний план задачі опуклого програмування. +
+ 
 (5.56)
(5.56) .
.



 , крім того
, крім того  , тобто нерівність справедлива лише у випадку, коли
, тобто нерівність справедлива лише у випадку, коли .
.

 , то приходимо до нерівності
, то приходимо до нерівності 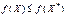 , яка справедлива для всіх значень
, яка справедлива для всіх значень  .
. задовольняє обмеження і надає максимального значення цільовій функції задачі, так як для всіх інших
задовольняє обмеження і надає максимального значення цільовій функції задачі, так як для всіх інших 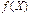 приймає менші значення ніж в точці
приймає менші значення ніж в точці  , тобто вона є оптимальним планом задачі нелінійного програмування. Достатність умов теореми доведено.
, тобто вона є оптимальним планом задачі нелінійного програмування. Достатність умов теореми доведено.


