
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Умови Куна-Такера для задач нелінійного програмування.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Умови теореми Куна — Таккера виконуються лише для задач, що містять опуклі функції. Опуклі й угнуті функції -Наведемо основні означення та теореми. Нехай задано n -вимірний лінійний простір Rn. Функція
Якщо нерівність строга і виконується для Функція Якщо нерівність строга і виконується для Слід зазначити, що опуклість та угнутість функції визначаються лише відносно опуклих множин у Теорема 8.2. Нехай Доведення. Допустимо, що в точці
Множина Х опукла, тому точка
Значення Теорема 8.3. Нехай Доведення. З рівності (8.12) для
Через те що існують частинні похідні першого порядку, функцію
де
Переходимо до границі при
Ця умова виконується для будь-яких внутрішніх точок Х 1 та Х 2 і є необхідною і достатньою умовою опуклості f (X). Якщо функція f (X) неперервна разом з частинними похідними першого порядку і угнута на множині Х, то аналогічно попередньому результату маємо:
Припустимо, що Х 0 — довільна точка множини Х, тоді, взявши
Отже, опукла функція f (X) досягає свого глобального мінімуму на множині Х у кожній точці, де Як наслідок теореми можна показати, що коли Х замкнена, обмежена знизу, опукла множина, то глобального максимуму опукла функція f (X) досягає на ній у одній чи кількох точках (при цьому допускається, що в точці Х значення функції скінченне). Застосовуючи за розв’язування таких задач процедуру перебору крайніх точок, можна отримати точку локального максимуму, однак не можна встановити, чи є вона точкою глобального максимуму. Для угнутих функцій отримані результати формулюють так. Нехай f (X) — угнута функція, що задана на замкненій опуклій множині Градієнт угнутої функції f (X) у точках максимуму дорівнює нулю, якщо f (X) — диференційовна функція. Глобальний мінімум угнутої функції, якщо він скінченний на замкненій обмеженій зверху множині, має досягатися в одній чи кількох її крайніх точках за умови скінченності функції f (X) у кожній точці цієї множини. Теорема Куна-Такера. Теорема Куна—Таккера дає змогу встановити типи задач, для яких на множині допустимих розв’язків існує лише один глобальний екстремум зумовленого типу. Вона тісно пов’язана з необхідними та достатніми умовами існування сідлової точки. Розглянемо задачу нелінійного програмування, яку, не зменшуючи загальності, подамо у вигляді:
(Очевидно, що знак нерівності можна змінити на протилежний множенням лівої і правої частин обмеження на (– 1)). Теорема 8.1. (Теорема Куна—Таккера). Вектор Х* є оптимальним розв’язком задачі (8.22)—(8.24) тоді і тільки тоді, коли існує такий вектор
і функція мети Доведення. Необхідність. Нехай Х* — оптимальний план задачі (8.22)—(8.24), тобто є точкою глобального максимуму задачі. Отже, для всіх інших планів задачі Х з множини допустимих розв’язків виконуватиметься співвідношення:
Розглянемо тепер вектор З умови (8.21) маємо:
Для точки з координатами
Функція Для встановлення нерівності, що відповідає лівій частині умови (8.13), а саме:
Отже, у точці Х * функція Лагранжа має глобальний максимум по Х, що повністю доводить необхідність теореми. Достатність. Для доведення достатності умов теореми потрібно виходити з того, що Підставимо у нерівність (8.13) вираз функції Лагранжа (8.12) для задачі (8.22)—(8.23):
при всіх значеннях Розглянемо праву частину подвійної нерівності (8.26).
Остання нерівність має виконуватися для всіх
Тоді з лівої частини нерівності (8.26) маємо:
Через те що Отже, точка Х * задовольняє обмеження і надає максимального значення цільовій функції задачі, тому що для всіх інших
|
||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 477; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.007 с.) |

 , що задана на опуклій множині
, що задана на опуклій множині  , називається опуклою, якщо для будь-яких двох точок
, називається опуклою, якщо для будь-яких двох точок  та
та 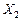 з множини X і будь-яких значень
з множини X і будь-яких значень  виконується співвідношення:
виконується співвідношення: . (8.27)
. (8.27) , то функція
, то функція  . (8.28)
. (8.28) , оскільки за наведеними означеннями разом з двома будь-якими точками
, оскільки за наведеними означеннями разом з двома будь-якими точками  для всіх значень
для всіх значень  функція
функція 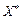 , отже, виконуватиметься нерівність
, отже, виконуватиметься нерівність  . Через те що
. Через те що 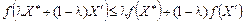 . (8.29)
. (8.29) при
при  ;
; .
. можна вибрати так, щоб точка
можна вибрати так, щоб точка  . Тоді в точці
. Тоді в точці 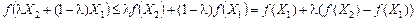 ;
;
 ;
;
 .
. можна розкласти в ряд Тейлора:
можна розкласти в ряд Тейлора: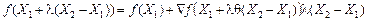 ,
, — градієнт функції f, обчислений у точці
— градієнт функції f, обчислений у точці  ,
,  . Тоді:
. Тоді:

 .
. , отримаємо:
, отримаємо:

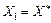 ,
,  , а також за умовою теореми
, а також за умовою теореми  , в нерівності (8.30) маємо:
, в нерівності (8.30) маємо:
 .
. , (8.22)
, (8.22) , (8.23)
, (8.23) . (8.24)
. (8.24) , що при
, що при  для всіх
для всіх  точка
точка 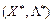 є сідловою точкою функції Лагранжа
є сідловою точкою функції Лагранжа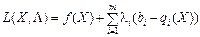 ,
, угнута, а функції
угнута, а функції  — опуклі.
— опуклі.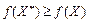 .
. , що відповідає точці глобального максимуму
, що відповідає точці глобального максимуму  ,
,  ,
,  , де
, де  — вектор множників Лагранжа, що відповідає Х.
— вектор множників Лагранжа, що відповідає Х. , тоді
, тоді . (8.25)
. (8.25) можуть бути відмінними від нуля. Оскільки за умовою задачі
можуть бути відмінними від нуля. Оскільки за умовою задачі  , то лише за умови, що
, то лише за умови, що  .
. — лінійна відносно
— лінійна відносно  , тобто остання нерівність виконується для будь-якого
, тобто остання нерівність виконується для будь-якого  — точка глобального мінімуму по
— точка глобального мінімуму по  , скористаємося також рівнянням (8.21), підсумувавши його по і:
, скористаємося також рівнянням (8.21), підсумувавши його по і:  . За умовою теореми
. За умовою теореми  — угнуті функції і
— угнуті функції і 
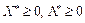 ,
,  — сідлова точка функції
— сідлова точка функції  (тобто для
(тобто для  (8.26)
(8.26) .
.


 .
. , тобто нерівність справджується лише у разі, коли
, тобто нерівність справджується лише у разі, коли .
.
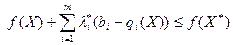 .
. , приходимо до нерівності
, приходимо до нерівності  , яка справджується для всіх значень
, яка справджується для всіх значень 


